贵州省毕节市大方县2022年中考数学模拟试题
试卷更新日期:2024-03-26 类型:中考模拟
一、选择题(共15小题,共45分)
-
1. 下列各数中,最小的数是( )A、 B、0 C、﹣1 D、22. 如图是由5个形状大小完全相同的小正方体搭成的几何体,若将小正方形A移到小正方体B的正上方,则关于该几何体变化前后的三视图,下列说法正确的是( )
 A、左视图不变 B、俯视图改变 C、主视图不变 D、以上三种视图都改变3. 下列计算正确的是( )A、 B、 C、 D、4. 2021年,祁阳成功实现撤县设市,迈上了阔步前行的新征程,翻开了跨越发展的新篇章,全市经济指标稳中向好,全年预计完成地区生产总值37300000000元,把数据37300000000用科学记数法表示为( )A、 B、 C、 D、5. 下列图形中既是轴对称图形,又是中心对称图形的是( )A、
A、左视图不变 B、俯视图改变 C、主视图不变 D、以上三种视图都改变3. 下列计算正确的是( )A、 B、 C、 D、4. 2021年,祁阳成功实现撤县设市,迈上了阔步前行的新征程,翻开了跨越发展的新篇章,全市经济指标稳中向好,全年预计完成地区生产总值37300000000元,把数据37300000000用科学记数法表示为( )A、 B、 C、 D、5. 下列图形中既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,△ABO的边OB在x轴的负半轴上,O是原点,点B的坐标为(-4,0),把△ABO沿x轴向右平移3个单位长度,得到△DCE , 连接AC , DO , 若△DOE的面积为6,则图中阴影部分△ACO的面积为( )
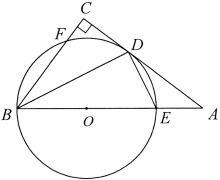
6. 如图,△ABO的边OB在x轴的负半轴上,O是原点,点B的坐标为(-4,0),把△ABO沿x轴向右平移3个单位长度,得到△DCE , 连接AC , DO , 若△DOE的面积为6,则图中阴影部分△ACO的面积为( ) A、1 B、2 C、3 D、47. 某中学七(1)班的6位同学在课间体育活动时进行一分钟跳绳比赛,成绩(单位:个)如下:122,176,134,164,176,162,这组数据的众数和中位数分别是( )A、162,164 B、176,140 C、176,149 D、176,1638. 如图,已知 的两条弦 , 相交于点E, , ,连接OE , 若E为AC中点,那么 的值为( )
A、1 B、2 C、3 D、47. 某中学七(1)班的6位同学在课间体育活动时进行一分钟跳绳比赛,成绩(单位:个)如下:122,176,134,164,176,162,这组数据的众数和中位数分别是( )A、162,164 B、176,140 C、176,149 D、176,1638. 如图,已知 的两条弦 , 相交于点E, , ,连接OE , 若E为AC中点,那么 的值为( )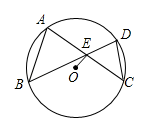 A、 B、 C、 D、9. 在2019年世界军人运动会中,我国军人运动员屡创佳绩,特别是在射击赛场获得很多金牌,如图是某项射击项目的射击靶示意图,其中每环的宽度与中心圆的半径相等,某运动员朝靶上任意射击一次没有脱靶,设其命中10、9、8、7的概率分别为、、、 , 则下列选项正确的是( ).
A、 B、 C、 D、9. 在2019年世界军人运动会中,我国军人运动员屡创佳绩,特别是在射击赛场获得很多金牌,如图是某项射击项目的射击靶示意图,其中每环的宽度与中心圆的半径相等,某运动员朝靶上任意射击一次没有脱靶,设其命中10、9、8、7的概率分别为、、、 , 则下列选项正确的是( ).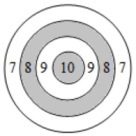 A、 B、 C、 D、10. 如图,点A是反比例函数图象上的一点,AB垂直x轴于点B , 若 , 则k的值为
A、 B、 C、 D、10. 如图,点A是反比例函数图象上的一点,AB垂直x轴于点B , 若 , 则k的值为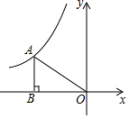 A、3 B、6 C、 D、11. 某校举行男女混合长跑接力赛,901班为参赛同学买了A,B两款运动服,A款共花费648元,B款共花费500元,A款比B款多2件,A款单价为B款的1.2倍. 若设B款的单价为x元,一根据题意可列方程为( )A、 B、 C、 D、12. 春意复苏,郑州绿化工程正在如火如荼地进行着,某工程队计划将一块长64m,宽40m的矩形场地建设成绿化广场如图,广场内部修建三条宽相等的小路,其余区域进行绿化.若使绿化区域的面积为广场总面积的80%,求小路的宽,设小路的宽为x m,则可列方程( )
A、3 B、6 C、 D、11. 某校举行男女混合长跑接力赛,901班为参赛同学买了A,B两款运动服,A款共花费648元,B款共花费500元,A款比B款多2件,A款单价为B款的1.2倍. 若设B款的单价为x元,一根据题意可列方程为( )A、 B、 C、 D、12. 春意复苏,郑州绿化工程正在如火如荼地进行着,某工程队计划将一块长64m,宽40m的矩形场地建设成绿化广场如图,广场内部修建三条宽相等的小路,其余区域进行绿化.若使绿化区域的面积为广场总面积的80%,求小路的宽,设小路的宽为x m,则可列方程( )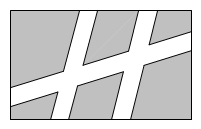 A、 B、 C、 D、13. 如图,在中,点D,E,F,G分别是线段BC,AB,BD,AD的中点,设四边形EFDG的面积为 , 则的面积为( )
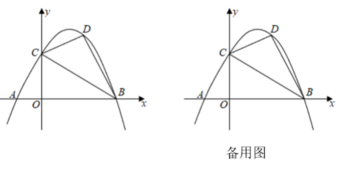
A、 B、 C、 D、13. 如图,在中,点D,E,F,G分别是线段BC,AB,BD,AD的中点,设四边形EFDG的面积为 , 则的面积为( )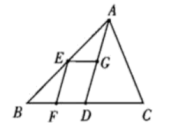 A、2S B、3S C、4S D、6S14. 已知二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+ac的图象和反比例函数y=的图象在同一坐标系中可能为( )
A、2S B、3S C、4S D、6S14. 已知二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+ac的图象和反比例函数y=的图象在同一坐标系中可能为( )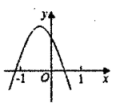 A、
A、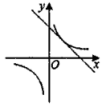 B、
B、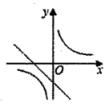 C、
C、 D、
D、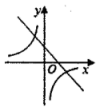 15. 如图,的斜边OB落在x轴上, , , 以O为圆心.OB长为半径作弧交OC的延长线于点D , 过点C作 , 交圆弧于点E . 若反比例函数的图像经过点E , 则k的值是( )
15. 如图,的斜边OB落在x轴上, , , 以O为圆心.OB长为半径作弧交OC的延长线于点D , 过点C作 , 交圆弧于点E . 若反比例函数的图像经过点E , 则k的值是( )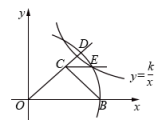 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共5小题,共25分)
-
16. 分解因式: .17. 函数的自变量x的取值范围是 .18. 已知x=2是关于x的一元二次方程x2+kx﹣2=0的一个根,则实数k的值为 .19. 如图是一张矩形纸片 , 点是对角线的中点,点在边上,把沿直线折叠,使点落在对角线上的点处,连接 , 若 , 则 度
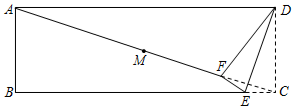 20. 如图,中, , D、E分别为中点,连接 , 则长为 .
20. 如图,中, , D、E分别为中点,连接 , 则长为 .
三、计算题
-
21. 解方程和不等式组:(1)、(2)、
四、解答题(本题共6小题,共70分)
-
22. 先化简,再求值: ,其中 .23. 随着2022年北京冬奥会的举办,冰雪运动在中国持续升温。为了调查学生对冰雪运动知识的了解情况,某校随机抽取部分学生进行了相关知识测试,获得了他们的成绩(百分制),根据调查结果绘制了如图尚不完整的统计图表:
组别
成绩分组(单位:分)
频数
频率
A
3
0.06
B
0.08
C
16
a
D
b
E
8
0.16
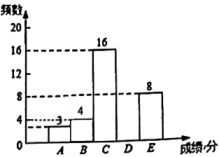
所抽取学生测试成绩在这一组的具体成绩是:80 80 81 81 82 82 82 83 83 84 84
85 85 86 86 86 87 88 89
根据以上信息,解答下列问题:
(1)、这次被调查的学生共有人, , 补全条形统计图;(2)、本次调查中,所抽取学生成绩的中位数是;(3)、该校共有学生1200人,若成绩在85分以上(含85分)的为优秀,假如全部学生参加此次测试,请估计该校学生成绩为优秀的人数.24. 如图,矩形ABCD的对角线AC与BD相交于点O,CEBD,DEAC,AD= , DE=2.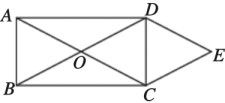 (1)、求证:四边形OCED是菱形;(2)、求四边形OCED的面积.25. 受疫情影响,运输受阻,某村一蔬菜种植大户大量蔬菜滞销,村书记联系各企事业单位团购,西红柿成本价为4元/千克,销售价为6元/千克;茄子成本价为5元/千克,销售价为8元/千克.通过团购,两种蔬菜共销售5000千克,其中西红柿的销售量不少于2000千克.(1)、若西红柿和茄子的总成本为22400元,分别求出西红柿和茄子的销售量.(2)、当西红柿的销售量为多少时,两种蔬菜的总利润最大?最大利润是多少?
(1)、求证:四边形OCED是菱形;(2)、求四边形OCED的面积.25. 受疫情影响,运输受阻,某村一蔬菜种植大户大量蔬菜滞销,村书记联系各企事业单位团购,西红柿成本价为4元/千克,销售价为6元/千克;茄子成本价为5元/千克,销售价为8元/千克.通过团购,两种蔬菜共销售5000千克,其中西红柿的销售量不少于2000千克.(1)、若西红柿和茄子的总成本为22400元,分别求出西红柿和茄子的销售量.(2)、当西红柿的销售量为多少时,两种蔬菜的总利润最大?最大利润是多少?
-