贵州省毕节市七星关区2022年中考数学模拟试题
试卷更新日期:2024-03-26 类型:中考模拟
一、选择题(共15小题,共45分)
-
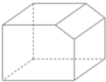
1. 在实数 , , 3.1415,中,无理数是( )A、 B、 C、3.1415 D、2. 如图所示的几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 《2021—2022中国大数据产业发展报告》预测,未来三年,我国大数据产业市场将保持12%以上的增速,到2023年整体规模将达到11522.5亿元.11522.5亿用科学记数法可以表示为( )A、 B、 C、 D、4. 下面的图形是用数学家的名字命名的,其中既是轴对称图形,又是中心对称图形的是( )A、赵爽弦图
3. 《2021—2022中国大数据产业发展报告》预测,未来三年,我国大数据产业市场将保持12%以上的增速,到2023年整体规模将达到11522.5亿元.11522.5亿用科学记数法可以表示为( )A、 B、 C、 D、4. 下面的图形是用数学家的名字命名的,其中既是轴对称图形,又是中心对称图形的是( )A、赵爽弦图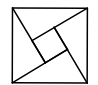 B、笛卡尔心形线
B、笛卡尔心形线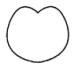 C、科克曲线
C、科克曲线 D、费马螺线
D、费马螺线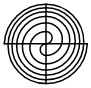 5. 如图,把一个直角三角尺的直角顶点放在直尺的一边上,若 , 则( )
5. 如图,把一个直角三角尺的直角顶点放在直尺的一边上,若 , 则( )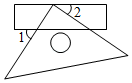 A、 B、 C、 D、6. 下列运算中,正确的是( ).A、 B、 C、 D、7. 若一个正多边形的每个内角都是120°,则这个正多边形是( )A、正六边形 B、正七边形 C、正八边形 D、正九边形8. 我国古代数学名著《孙子算经》记载一道题:“一百马,一百瓦,大马一个拖三个,小马三个拖一个”,大意为:100匹马拉100片瓦,已知1个大马拖3片瓦,3匹小马拖一片瓦,问有多少匹大马,多少匹小马?若设有m匹大马,n匹小马,那么可列方程组为( )A、 B、 C、 D、9. 小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,把手AM的仰角α=37°,此时把手端点A、出水口点B和落水点C在同一直线上,洗手盆及水龙头的相关数据如图2,则线段CH长是( )(参考数据: , , )
A、 B、 C、 D、6. 下列运算中,正确的是( ).A、 B、 C、 D、7. 若一个正多边形的每个内角都是120°,则这个正多边形是( )A、正六边形 B、正七边形 C、正八边形 D、正九边形8. 我国古代数学名著《孙子算经》记载一道题:“一百马,一百瓦,大马一个拖三个,小马三个拖一个”,大意为:100匹马拉100片瓦,已知1个大马拖3片瓦,3匹小马拖一片瓦,问有多少匹大马,多少匹小马?若设有m匹大马,n匹小马,那么可列方程组为( )A、 B、 C、 D、9. 小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,把手AM的仰角α=37°,此时把手端点A、出水口点B和落水点C在同一直线上,洗手盆及水龙头的相关数据如图2,则线段CH长是( )(参考数据: , , )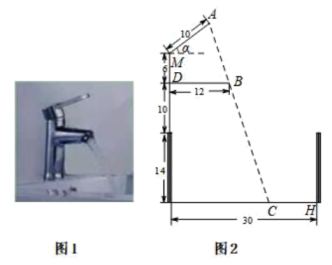 A、9 B、8 C、10 D、1110. 若关于x的方程是一元二次方程,则m的取值范围是( )A、 B、 C、 D、11. 为了完成下列任务,你觉得采用抽样调查更合适的是( )A、了解某校七年级(1)班全体学生每天的睡眠时长 B、神舟十三号载人飞船发射之前,对各部分零部件进行检测 C、了解某同学一周每天练习跳绳的时长 D、中央电视台《开学第一课》的收视率12. 在数学跨学科主题活动课上,芳芳用半径 , 圆心角的扇形纸板,做了一个圆锥形的生日帽,如图所示.在不考虑接缝的情况下,这个圆锥形生日帽的底面圆半径是( )
A、9 B、8 C、10 D、1110. 若关于x的方程是一元二次方程,则m的取值范围是( )A、 B、 C、 D、11. 为了完成下列任务,你觉得采用抽样调查更合适的是( )A、了解某校七年级(1)班全体学生每天的睡眠时长 B、神舟十三号载人飞船发射之前,对各部分零部件进行检测 C、了解某同学一周每天练习跳绳的时长 D、中央电视台《开学第一课》的收视率12. 在数学跨学科主题活动课上,芳芳用半径 , 圆心角的扇形纸板,做了一个圆锥形的生日帽,如图所示.在不考虑接缝的情况下,这个圆锥形生日帽的底面圆半径是( )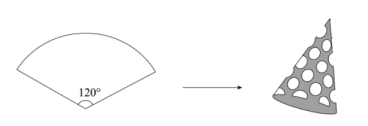 A、 B、 C、 D、13. 早期,甲肝流行,在一天内,一人能传染4人,若有三人患上甲肝,那么经过两天患上甲肝的人数为( )A、50 B、75 C、25 D、7014. 如图,把一张长方形纸片沿EF折叠后,点D、C分别落在点、的位置,若 , 则( ).
A、 B、 C、 D、13. 早期,甲肝流行,在一天内,一人能传染4人,若有三人患上甲肝,那么经过两天患上甲肝的人数为( )A、50 B、75 C、25 D、7014. 如图,把一张长方形纸片沿EF折叠后,点D、C分别落在点、的位置,若 , 则( ). A、65° B、70° C、75° D、80°15. 如图,抛物线(是常数,)的顶点在第四象限,对称轴是 , 过一、二、四象限的直线(是常数)与抛物线交于轴上一点,则下列结论正确的有( )个.
A、65° B、70° C、75° D、80°15. 如图,抛物线(是常数,)的顶点在第四象限,对称轴是 , 过一、二、四象限的直线(是常数)与抛物线交于轴上一点,则下列结论正确的有( )个.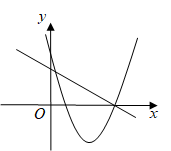
① , ② , ③ , ④当抛物线与直线的另一个交点也在坐标轴上时,则 , ⑤为任意实数,则有 .
A、2 B、3 C、4 D、5二、填空题(共5小题,共25分)
-
16. 若将一次函数y=x+b的图象向右平移4个单位后,经过点P(3,0),则b= .17. 如图,一条河的两岸有一段是平行的,在河的南岸岸边每隔5m有一棵树,小华站在离南岸20m的点P处看北岸,在两棵树之间的空隙中,恰好看见一条龙舟的龙头和龙尾(假设龙头、龙尾和小华的眼睛位于同一水平平面内),已知龙舟的长为18.5m,若龙舟行驶在河的中心,且龙舟与河岸平行,则河宽为m.
 18. 如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,BC的中点,连接EF.按以下步骤作图:①分别以点O,C为圆心,大于OC的长为半径作弧,两弧交于点P;②作直线PF,交AC于点G.若AD=4 , BD=8,则线段EF的长为 .
18. 如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,BC的中点,连接EF.按以下步骤作图:①分别以点O,C为圆心,大于OC的长为半径作弧,两弧交于点P;②作直线PF,交AC于点G.若AD=4 , BD=8,则线段EF的长为 .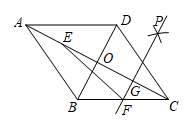 19. 直线与x轴交于点D , 与y轴交于点 , 把正方形、和按如图所示方式放置,点、在直线上,点、、在x轴上,按照这样的规律,则正方形中的点的坐标为 .
19. 直线与x轴交于点D , 与y轴交于点 , 把正方形、和按如图所示方式放置,点、在直线上,点、、在x轴上,按照这样的规律,则正方形中的点的坐标为 .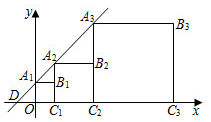 20. 如图,在平面直角坐标系中,O是坐标原点,直线向下平移b个单位后与反比例函数交第一象限于点A , 交x轴于B点, , , 则 .
20. 如图,在平面直角坐标系中,O是坐标原点,直线向下平移b个单位后与反比例函数交第一象限于点A , 交x轴于B点, , , 则 .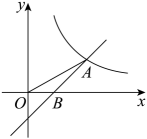
三、解答题(本题共7小题,共80分)
-
21.(1)、计算:-|-3|+2cos45°+(-1)2019-(2)、化简:22. 解下列不等式组,并在数轴上表示解集: .
 23. 山西是我国现存各类古建筑最多的省份,据不完全统计,重点记录在册的就有1万8千余处,上迄唐代,下至民国,构成了我国建筑史上品质超群、蔚为壮观的建筑体系,享有“中国古代建筑博物馆”之美誉.某中学对本校学生开展了“我最喜欢的山西古代建筑”的随机抽样调查(每人只能选一项):A . 万荣东岳庙飞云楼,B . 朔州崇福寺弥陀殿,C . 五台佛光寺东大殿,D . 太原晋柯圣母殿,E . 榆次城隍庙玄鉴楼.根据收集的数据绘制了如图所示的两幅不完整的统计图,其中B对应的圆心角为90°,请根据图中信息解答下列问题.
23. 山西是我国现存各类古建筑最多的省份,据不完全统计,重点记录在册的就有1万8千余处,上迄唐代,下至民国,构成了我国建筑史上品质超群、蔚为壮观的建筑体系,享有“中国古代建筑博物馆”之美誉.某中学对本校学生开展了“我最喜欢的山西古代建筑”的随机抽样调查(每人只能选一项):A . 万荣东岳庙飞云楼,B . 朔州崇福寺弥陀殿,C . 五台佛光寺东大殿,D . 太原晋柯圣母殿,E . 榆次城隍庙玄鉴楼.根据收集的数据绘制了如图所示的两幅不完整的统计图,其中B对应的圆心角为90°,请根据图中信息解答下列问题.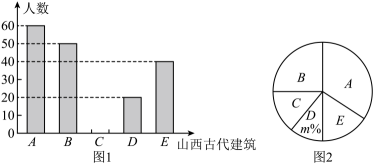 (1)、抽取的本校学生共有人,并补全条形统计图 .(2)、扇形统计图中m= , 表示D的扇形的圆心角是°.(3)、若该校有学生1000人,请根据抽样调查结果估算该校最喜欢古代建筑E的学生人数.(4)、校方准备在最喜欢古代建筑A的5名学生中随机选择2名进行实地考察,这5名学生中有2名男生和3名女生,请用画树状图或列表的方法求选出的2名学生都是女生的概率.24. 课外兴趣小组活动时,老师提出了如下问题:
(1)、抽取的本校学生共有人,并补全条形统计图 .(2)、扇形统计图中m= , 表示D的扇形的圆心角是°.(3)、若该校有学生1000人,请根据抽样调查结果估算该校最喜欢古代建筑E的学生人数.(4)、校方准备在最喜欢古代建筑A的5名学生中随机选择2名进行实地考察,这5名学生中有2名男生和3名女生,请用画树状图或列表的方法求选出的2名学生都是女生的概率.24. 课外兴趣小组活动时,老师提出了如下问题: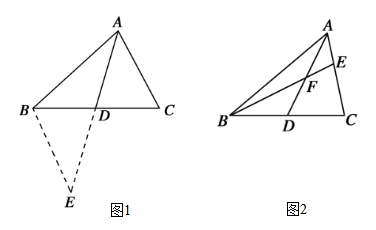 (1)、如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考帮小明完成解答过程.(2)、如图2,AD是△ABC的中线,BE交AC干E,交AD于F,且AE=EF.请判昕AC与BF的数量关系,并说明理由.25. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D,点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到点C时,两点都停止运动,设运动时间为t秒.
(1)、如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考帮小明完成解答过程.(2)、如图2,AD是△ABC的中线,BE交AC干E,交AD于F,且AE=EF.请判昕AC与BF的数量关系,并说明理由.25. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D,点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到点C时,两点都停止运动,设运动时间为t秒. (1)、求线段CD的长;(2)、设△CPQ的面积为S,求S与t之间的函数关系式,并写出自变量的取值范围;(3)、当t为何值时,△CPQ与△CAD相似?请直接写出t的值.26. 如图,已知 , 是的平分线,是射线上一点, . 动点从点出发,以的速度沿水平向左作匀速运动,与此同时,动点从点出发,也以的速度沿竖直向上作匀速运动.连接 , 交于点 . 经过、、三点作圆,交于点 , 连接、 . 设运动时间为 , 其中 .
(1)、求线段CD的长;(2)、设△CPQ的面积为S,求S与t之间的函数关系式,并写出自变量的取值范围;(3)、当t为何值时,△CPQ与△CAD相似?请直接写出t的值.26. 如图,已知 , 是的平分线,是射线上一点, . 动点从点出发,以的速度沿水平向左作匀速运动,与此同时,动点从点出发,也以的速度沿竖直向上作匀速运动.连接 , 交于点 . 经过、、三点作圆,交于点 , 连接、 . 设运动时间为 , 其中 .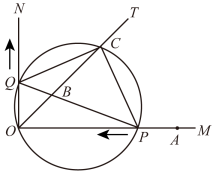 (1)、求的值;(2)、是否存在实数t , 使得线段的长度最大?若存在,求出t的值;若不存在,说明理由.(3)、在点P , 点Q运动过程中,四边形的面积是否发生改变,如果变,请说明理由;如果不变,请求出四边形的面积.27. 如图,在中, , 以为直径的交于点 , 过点作 , 垂足为 , 交的延长线于 , 过点作 , 垂足为 , 连接 .
(1)、求的值;(2)、是否存在实数t , 使得线段的长度最大?若存在,求出t的值;若不存在,说明理由.(3)、在点P , 点Q运动过程中,四边形的面积是否发生改变,如果变,请说明理由;如果不变,请求出四边形的面积.27. 如图,在中, , 以为直径的交于点 , 过点作 , 垂足为 , 交的延长线于 , 过点作 , 垂足为 , 连接 .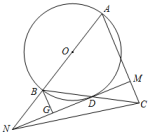 (1)、求证:直线是的切线;(2)、求证:;(3)、若 , 求的值.
(1)、求证:直线是的切线;(2)、求证:;(3)、若 , 求的值.