贵州省六盘水市钟山区2023-2024学年九年级上学期数学期末考试试卷
试卷更新日期:2024-03-26 类型:期末考试
一、选择题(每小题3分,共36分.每小题均有A、B、C、D四个选项,其中只有一个选项正确)
-
1. 的绝对值是( )A、 B、 C、 D、2. 下列几何体中,主视图、左视图、俯视图都相同的是( )A、
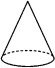 B、
B、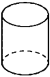 C、
C、 D、
D、 3. 习近平总书记在2024年新年贺词中点赞“村超”.2023年5月13日,贵州省榕江县举办了“和美乡村足球超级联赛”即为“村超”.该比赛迎来了全国各地的游客.据了解,5月份榕江县共接待游客1073700人次.1073700这个数用科学记数法表示正确的是( )A、 B、 C、 D、4. 中华汉字,寓意深广.下列四个选项中,是轴对称图形的是( )A、
3. 习近平总书记在2024年新年贺词中点赞“村超”.2023年5月13日,贵州省榕江县举办了“和美乡村足球超级联赛”即为“村超”.该比赛迎来了全国各地的游客.据了解,5月份榕江县共接待游客1073700人次.1073700这个数用科学记数法表示正确的是( )A、 B、 C、 D、4. 中华汉字,寓意深广.下列四个选项中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 下表是我市某校九(1)班参加学校“纪念12.9主题演讲活动”的得分情况,表中“得分”数据的中位数是( )
5. 下表是我市某校九(1)班参加学校“纪念12.9主题演讲活动”的得分情况,表中“得分”数据的中位数是( )评委
评委1
评委2
评委3
评委4
评委5
评委6
评委7
得分
9.6
9.4
9.5
9.6
9.4
9.6
9.3
A、9.3 B、9.4 C、9.5 D、9.66. 如图,与位似,点O为位似中心,已知 , 则AC与DF的比是( ) A、3:2 B、5:3 C、5:2 D、3:57. 有6张完全相同的卡片,每张卡片的正面都写有一种常见的生活现象,将所有卡片背面朝上,从中任意抽出一张,抽到的“生活现象”只有物理变化的概率是( )
A、3:2 B、5:3 C、5:2 D、3:57. 有6张完全相同的卡片,每张卡片的正面都写有一种常见的生活现象,将所有卡片背面朝上,从中任意抽出一张,抽到的“生活现象”只有物理变化的概率是( ) A、 B、 C、 D、8. 如图所示,点P表示数轴上的一个无理数,这个无理数最接近的是( )
A、 B、 C、 D、8. 如图所示,点P表示数轴上的一个无理数,这个无理数最接近的是( ) A、 B、 C、 D、9. 如图,在中, , 以点B为圆心,任意长为半径画弧,分别与AB , BC交于点D , E , 再分别以点D , E为圆心,大于的长为半径画弧,两弧在内交于点F , 作射线BF交AC于点G , 过点G作于点H . 若 , , 则的面积是( )
A、 B、 C、 D、9. 如图,在中, , 以点B为圆心,任意长为半径画弧,分别与AB , BC交于点D , E , 再分别以点D , E为圆心,大于的长为半径画弧,两弧在内交于点F , 作射线BF交AC于点G , 过点G作于点H . 若 , , 则的面积是( ) A、 B、 C、 D、110. 已知:a , b是方程的两个实数根,则( )A、 B、 C、 D、11. 如图所示,小明用七巧板拼成一个对角线长为4的正方形,再用这副七巧板拼成一个长方形,则长方形的对角线长为( )
A、 B、 C、 D、110. 已知:a , b是方程的两个实数根,则( )A、 B、 C、 D、11. 如图所示,小明用七巧板拼成一个对角线长为4的正方形,再用这副七巧板拼成一个长方形,则长方形的对角线长为( ) A、4 B、 C、 D、512. 如图,是利用一把直尺和一块三角尺ABC摆放并移动后得到的图形,其中 , , , 点A对应直尺的刻度为12,将该三角尺沿直尺边缘平移,使移动到 , 点对应直尺的刻度为0,则点C到的距离是( )
A、4 B、 C、 D、512. 如图,是利用一把直尺和一块三角尺ABC摆放并移动后得到的图形,其中 , , , 点A对应直尺的刻度为12,将该三角尺沿直尺边缘平移,使移动到 , 点对应直尺的刻度为0,则点C到的距离是( )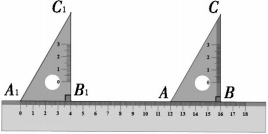 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题4分,共16分)
-
13. 钟山区2023年12月某天的最高温度是9℃,最低温度是℃,则这天的温差是℃.14. 2023年11月,我国某品牌新能源汽车的销量为64万辆,预计2024年1月销量达到81万辆,设该厂销售月平均增长率为x , 则 .15. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交于点P , 点F为焦点,若 , , 则 .
 16. 正三角形ABC的边长为1,D是BC边上的一点(点D不与点B、C重合),过点D作AB边的垂线,交AB于点G , 用x表示线段AG的长度,的面积y是x的函数,则该函数的表达式是(要求写出自变量x的取值范围)
16. 正三角形ABC的边长为1,D是BC边上的一点(点D不与点B、C重合),过点D作AB边的垂线,交AB于点G , 用x表示线段AG的长度,的面积y是x的函数,则该函数的表达式是(要求写出自变量x的取值范围)三、解答题(本大题共9题,共98分.解答应写出必要的文字说明、证明过程和演算步骤)
-
17.(1)、计算:;(2)、已知: , , 当时,求a的值.18. 下面是一道例题及其解答过程的一部分,其中M是整式,请写出整式M , 并写出完整的解答过程.
例:先化简,再求值: , 其中
解:原式 .
……
(1)、整式;(2)、请写出完整的解答过程.19. 诗词从来不是曲高和寡的阳春白雪,而是无数中国人“日用而不知”的精神滋养之所在.某学校组织九年级学生参加“黔城读书月诗词大赛”区级选拔赛.为了解该年级学生参赛成绩的情况,随机抽取了一部分学生的成绩,分成四组:A:;B:;C:;D: , 并绘制出如下统计图.

解答下列问题:
(1)、本次调查的学生共有多少人?请补全条形统计图;(2)、学校将从D组最优秀的4名学生甲、乙、丙、丁中随机选取2人参加下一轮比赛,利用画树状图或列表得方法,求刚好抽到甲和丁参赛的概率.20. 如图,在矩形ABCD中,点E是BC的中点,连接AE , 过点D作AE的垂线分别交AE , AB于点F , G . (1)、求证:;(2)、若 , , 求AE的长.21. 如图,一次函数的图象与反比例函数的图象交于点 , .
(1)、求证:;(2)、若 , , 求AE的长.21. 如图,一次函数的图象与反比例函数的图象交于点 , . (1)、求一次函数的表达式;(2)、已知点 , 试求与的数量关系.22. 风电项目对于调整能源结构和转变经济发展方式具有重要意义.钟山电力部门在贵州屋脊乌蒙山韭菜坪一坡角为20°()的坡地上新安装了一架风力发电机,如图①,为了解这架风力发电机的塔杆高度,某校数学组组织数学兴趣小组进行了实地测量.图②为测量示意图,测得斜坡BD长为57米,在地面观测,点D处测得风力发电机塔杆顶端A的仰角为59°.(参考数据: , , )
(1)、求一次函数的表达式;(2)、已知点 , 试求与的数量关系.22. 风电项目对于调整能源结构和转变经济发展方式具有重要意义.钟山电力部门在贵州屋脊乌蒙山韭菜坪一坡角为20°()的坡地上新安装了一架风力发电机,如图①,为了解这架风力发电机的塔杆高度,某校数学组组织数学兴趣小组进行了实地测量.图②为测量示意图,测得斜坡BD长为57米,在地面观测,点D处测得风力发电机塔杆顶端A的仰角为59°.(参考数据: , , )图①
 图②
图② (1)、求CD的长(结果保留一位小数);(2)、求该风力发电机塔杆AB的高度(结果保留整数).23. 为抢抓大数据产业发展先机,紧跟电商发展新机遇、新模式、新业态,贵州省大力打造地方特色电商平台,通过“云”销售,助力“黔货出山”.贵州特产某品牌维C刺梨汁的进价为45元/箱,售价为60元/箱,某销售网店平均每周可售出100箱;而当销售价每降低1元时,平均每周多售出20箱.设每箱产品降价x元,每个周的销售利润为y元(1)、求y与x的关系式;(2)、当销售价为多少元时,每周获得的利润最大?并求出最大利润.24. 如图,在四边形ABCD中, , , , , .
(1)、求CD的长(结果保留一位小数);(2)、求该风力发电机塔杆AB的高度(结果保留整数).23. 为抢抓大数据产业发展先机,紧跟电商发展新机遇、新模式、新业态,贵州省大力打造地方特色电商平台,通过“云”销售,助力“黔货出山”.贵州特产某品牌维C刺梨汁的进价为45元/箱,售价为60元/箱,某销售网店平均每周可售出100箱;而当销售价每降低1元时,平均每周多售出20箱.设每箱产品降价x元,每个周的销售利润为y元(1)、求y与x的关系式;(2)、当销售价为多少元时,每周获得的利润最大?并求出最大利润.24. 如图,在四边形ABCD中, , , , , . (1)、求证:四边形ABCD时菱形;(2)、延长BC至点M , 连接OM交CD于点N , 若 , 求 .25. 我们知道,求两个一次函数图象的交点坐标时,可联立两个一次函数表达式组成方程组,方程组的解就是两个一次函数图象交点的坐标.类似的,我们解决二次函数图象与直线的交点问题时,也可以用同样的方法求解.
(1)、求证:四边形ABCD时菱形;(2)、延长BC至点M , 连接OM交CD于点N , 若 , 求 .25. 我们知道,求两个一次函数图象的交点坐标时,可联立两个一次函数表达式组成方程组,方程组的解就是两个一次函数图象交点的坐标.类似的,我们解决二次函数图象与直线的交点问题时,也可以用同样的方法求解.下面是通过方程思想解决二次函数()图象与一次函数()图象的交点情况的部分探究过程:联立方程组得 ,
整理得: , ∵
∴方程是关于x的一元二次方程,则 ,
当时,方程有两个不相等的实数根,
∴二次函数的图象与一次函数的图象有两个交点.
任务:
(1)、请参照文中时的分析过程,直接写出当和时的二次函数()图象与一次函数()图象的交点情况;(2)、若二次函数的图象与一次函数的图象有两个交点,求c的取值范围;(3)、当(2)中的c取最小正整数时,直接写出不等式的解集.