贵州省铜仁市2023-2024学年九年级上学期数学期末考试试卷

试卷更新日期：2024-03-26 类型：期末考试

进入出卷网下载

一、选择题（本题共12个小题，每小题3分，共36分．本题每小题均有A、B、C、D四个备选答案，其中只有一个是正确的，请你将正确答案填涂在相应的答题卡上）

1. 把一元二次方程 $3 x^{2} = 4 x - 1$ 化为一般式，当二次项为 $3 x^{2}$ 时，一次项和常数项分别为（）

A、 $4 x$ ， $- 1$ B、 $4 x$ ， 1 C、 $- 4 x$ ， $- 1$ D、 $- 4 x$ ， 1

查看试题解析
2. 当 $a > b$ 时，反比例函数 $y = \frac{a - b}{x}$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
3. 近期有300人参加了某地举办的非遗传承项目—仡佬族印染的培训活动，活动结束，每位学员必须提交一件用所学技法制作的印染作品．组织方从中抽查的30名学员作品通过专家组评判，不合格率仅为 $2 %$ ．根据抽查结果可以预测，这300名学员作品合格率是（）

A、 $20 %$ B、 $80 %$ C、 $2 %$ D、 $98 %$

查看试题解析
4. 如图是某景区大门部分建筑，已知 $A D ∥ B E ∥ C F$ ， $A C = 16 m$ ，当 $D F : D E = 4 : 3$ 时，则 $A B$ 的长是（）

A、 $10 m$ B、 $11 m$ C、 $12 m$ D、 $13 m$

查看试题解析
5. 德江某板鸭加工厂，为调查一批旱鸭的品质，从中随机选取了4只，以斤为计量单位（1斤等于500克），记录其质量分别为6斤、7斤、8斤、7斤，则估计这批旱鸭质量的方差是（）

A、 $1.5$ B、 $0.5$ C、7 D、4

查看试题解析
6. 如图，在平面直角坐标系中，两个大小不一的铜仁城市标识图案是位似图形，原点O是位似中心，点A、B的对应点分别是点C、D ，已知点A的坐标是 $(12, 6)$ ， $\frac{A B}{C D} = 3$ ，则点C的坐标为（）

A、 $(4, 2)$ B、 $(2, 4)$ C、 $(6, 3)$ D、 $(3, 6)$

查看试题解析
7. 小明看完“上刀山”表演后，被表演艺人精湛技艺所震撼，他发现，艺人在如图大刀的 $A B$ 段表演时最精彩，他想利用所学知识测量一下B点的高度，已知点P、A、B在一条直线上，点P、C、D也在一条直线上， $A C ⊥ P D$ ， $B D ⊥ P D$ ， $A C = C D = 2 m$ ，大刀的坡度（即 $∠ A P C$ 的坡度）为 $i = \frac{1}{2}$ ，则 $B D$ 为（）

A、 $2 m$ B、 $3 m$ C、 $4 m$ D、 $5 m$

查看试题解析
8. 如图，在 $R t △ A B C$ 中，以点A为圆心，适当长为半径作弧，交 $A B$ 于点E ，交 $A C$ 于点F ，分别以点E ， F为圆心，大于 $\frac{1}{2} E F$ 的长为半径作弧，两弧在 $∠ B A C$ 内部交于点G ，作射线 $A G$ 交 $B C$ 于点D ．若 $A C = 4$ ， $t a n ∠ B A D = \frac{1}{3}$ ，则 $C D$ 的长是（）

A、 $\frac{3}{4}$ B、1 C、 $\frac{4}{3}$ D、2

查看试题解析
9. “黔绣”的技师擅长在叶脉上飞针走绣，巧妙地将传统刺绣图案与树叶天然纹理完美结合，创作出神奇的“叶脉苗绣”作品．实际上，很多叶片本身都蕴含着黄金分割的比例，在大自然中呈现出优美的样子．如图，点P大致是 $A B$ 的黄金分割点 $(A P > P B)$ ，如果 $A P$ 的长为 $4 c m$ ，那么 $A B$ 的长约为（）

A、 $(2 \sqrt{5} + 2) c m$ B、 $(2 \sqrt{5} - 2) c m$ C、 $(2 \sqrt{5} + 1) c m$ D、 $(2 \sqrt{5} - 1) c m$

查看试题解析
10. 得天独厚的自然条件和生态资源，已让铜仁这片黔东沃土孕育出33个地理标志产品．在2023梵净山国际地理标志研讨会议召开之际，某区举行地理标志产品知识竞赛，如图使用 $S_{矩形 A B C O}$ 、 $S_{矩形 D E F O}$ 、 $S_{矩形 G H I O}$ 、 $S_{矩形 J K L O}$ 分别描述了甲、乙、丙、丁四个社区居民竞赛成绩的优秀人数，已知y表示社区居民竞赛成绩的优秀率，x表示该社区参赛居民人数，占B和点K在同一条反比例函数图象上，则这四个社区在这次知识竞赛中优秀人数最多的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
11. 某城市为增加绿植面积，改造部分室外停车位，如图①所示，6个车位拼成的矩形阴影部分全部为绿色草坪，当所有的车位分割线及停车方向线等标线粗细全部忽略不计时，可以看成图②，已知绿色草坪横条和竖条均为矩形，且宽度都为 $a m$ ， $A B = 12 m$ ， $B C = 7.2 m$ ，当草坪面积（图中阴影部分面积）等于 $40.2 m^{2}$ 时，则a的值是（）

A、 $0.75 m$ B、 $1 m$ C、 $1.2 m$ D、 $1.5 m$

查看试题解析
12. 已知如图，反比例函数 $y = - \frac{4}{x}$ ， $y = \frac{6}{x}$ 的图象分别经过正方形 $D E O F$ 、正方形 $A C O B$ 的顶点D、A ，连接 $E F 、 A E 、 A F$ ，则 $△ A E F$ 的面积等于（）

A、2 B、3 C、1 D、5

查看试题解析

二、填空题（本题共4个小题，每小题4分，共16分）

13. 已知点 $(2, - 3)$ 和点 $(1, m)$ 都在同一个反比例函数图象上，则m的值为．

查看试题解析
14. 关于x的一元二次方程 $a x^{2} - 8 x + b = 0$ 有两个相等的实数根，a与b的乘积是．

查看试题解析
15. 如图所示，某种品牌小轿车左右两个参照点A和F的距离为 $1.8$ 米，这两个参照点到地面 $B E$ 的距离 $A C = F D = 1.2$ 米，若驾驶员的眼睛点P到地面 $B E$ 的距离 $P G = 1.5$ 米，则驾驶员的视野盲区 $B E$ 的长度为米．

查看试题解析
16. 如图，正方形纸片 $A B C D$ 的边长为6，点E是边 $C D$ 上一定点，连接 $A E$ ，且 $s i n ∠ D A E = \frac{\sqrt{5}}{5}$ ，点F是边 $A D$ 的中点，点M是线段 $A F$ （除点A外）上任意一个动点，连接 $B M$ ，把 $△ A B M$ 沿 $B M$ 折叠，点A落在 $A^{'}$ 处，连接 $A^{'} E$ ，则 $A^{'} E$ 的最小值是．

查看试题解析

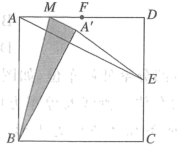
三、解答题（本题共9个小题，第17、19、20、21、22题每小题10分，第18、23、24、25题每小题12分，共98分，要有解题的主要过程）

17.

(1)、根据个人爱好，从 $s i n 30 °$ ， $c o s 45 °$ 和 $t a n 60 °$ 中任取两个，然后求选取的两个三角函数的平方和；

(2)、采用配方法或公式法解一元二次方程 $x^{2} + 4 x - 5 = 0$ ．

查看试题解析
18. 为了让初中生更加直观的体验非遗手工技艺，感受非遗文化的独特魅力，培养他们对优秀传统文化的兴趣，积极参与到非物质文化遗产的保护和传承中来，某校举办了非遗知识进课堂活动，选定木偶戏、四面花鼓、说春、船工号子四类非遗项目，随机抽查了部分学生，要求每名学生从中选择自己最喜欢的非遗项目，将抽查结果绘制成如下统计图（不完整）．
请根据图中信息解答下列问题：

(1)、被抽查的学生人数为，并将条形统计图补充完整．（温馨提醒：请画在答题卡相对应的图上）；

(2)、若该校共有1200名学生，根据抽查结果，试估计全校最喜欢“木偶戏”的学生人数；

(3)、该学校计划选定其中一个非遗项目创建特色课堂，你对具体选择什么项目有没有建议，请写出1条合理性的建议．

查看试题解析
19. 石阡是“中国苔茶之乡”，是茶树的原产地之一，有千年的茶叶栽种历史．某次茶艺比赛中指定使用的饮水机4分钟就可以将 $20 ℃$ 的饮用水加热到 $100 ℃$ ．此后停止加热，水温开始下降．如图所示，已知整个下降过程中水温 $y (℃)$ 与通电时间 $x (m i n)$ 成反比例关系．

(1)、在水温下降过程中，求y与x的函数解析式；

(2)、比赛组织方要求，参赛选手必须把组织方提供的 $20 ℃$ 的饮用水用该款饮水机加热到 $100 ℃$ ，然后降温到 $80 ℃$ 方可使用．求从饮水机加热开始，到可以使用需要等待多长时间？

查看试题解析
20. 已知如图，在 $△ A B C$ 中，点D是 $A B$ 边上一个动点，连接 $C D$ ，在 $C D$ 的右侧作 $∠ C D E$ ， $D E$ 边交 $B C$ 于点E ，当点D在 $A B$ 边上运动时（点D不与点A、点B重合），始终保持 $∠ A = ∠ C D E$ ．

(1)、你能否再添加一个条件，使 $△ A C D ∽ △ B D E$ ；

(2)、在（1）的条件下，当 $A C = 4$ ， $B E = 3$ ， $A B = 8$ 时，求A、D两点之间的距离．

查看试题解析
21. 大白将如图某个棱长为 $8 c m$ 正方体木块固定于水平木板 $O B$ 上， $O A = 20 c m$ ，将木板 $O B$ 绕端点O旋转 $36 °$ 至 $O B^{^{'}}$ （即 $∠ B O B^{'} = 36 °$ ）， $B^{'} E ⊥ O B$ 于点E ，交 $C D$ 于点 $F$ ， $C^{'} G ⊥ E B^{'}$ 延长线于点G ．

(1)、求点 $B^{'}$ 到 $O B$ 的距离；

(2)、在（1）问的基础上求点C竖直方向上抬升的高度．（参考数据： $s i n 36 ° \approx 0.59$ ， $c o s 36 ° \approx 0.81$ ， $t a n 36 ° \approx 0.73$ ．（1）（2）题中结果精确到个位）

查看试题解析
22. 如图①，一次函数 $y = \frac{1}{2} x + 2$ 的图象与 $y$ 轴交于点 $A$ ，点 $B$ 是反比例函数 $y = \frac{6}{x}$ 的图象与一次函数 $y = \frac{1}{2} x + 2$ 的图象在第一象限的交点．

(1)、求点B的坐标；

(2)、点 $C$ 是反比例函数 $y = \frac{6}{x}$ 在第一象限内的图象上有别于 $B$ 的另外一点，过点 $C$ 作 $C D$ $∥ A B$ 交 $x$ 轴于点 $D$ ．在 $x$ 轴正半轴上是否存在一点 $D$ ，使四边形 $A B C D$ 是平行四边形，如果存在，请确定 $A D$ 的长度，如果不存在，请说明理由．

查看试题解析
23. 已知如图， $R t △ A B C$ 中， $∠ C = 90 °$ ， $B C = 20 c m$ ， $s i n B = \frac{3}{5}$ ， E、F分别是边 $A B 、 B C$ 上的动点，点E从A向B匀速运动，点F从B向C匀速运动，E、F运动速度均为 $1 c m / s$ ，连接 $E F 、 C E$ ．

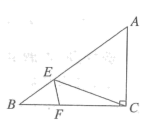(1)、求 $A B$ 的长；

(2)、当点E与点F同时开始运动，t秒后， $△ B E F ∽ △ B C A$ （点E与点C是对应点），请求出t的值．

查看试题解析
24. 近年来，某文创团队充分利用铜仁非遗项目种类繁多的资源优势，用心打造的A商品—投入市场，就深受广大游客喜爱．已知A商品每件成本60元，经调查发现，定价为每件100元时，一天可以卖出120件，每降价1元，就多卖出5件．

(1)、设A商品降价x元，则一天可以卖出件（用含x的式子表示）；

(2)、该文创团队一天能获得5100元利润吗？如果能，则需要降价多少元？如果不能，请说明理由．

查看试题解析
25. 在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 3$ ， $B C = 4$ ，将 $△ A B C$ 绕点C逆时针旋一个角度 $α$ 得到 $R t △ A^{'} B^{'} C$ ，连接 $A A^{'}$ ， $B B^{'}$ ．

(1)、如图①，当 $0 ° < α < 90 °$ 时，求证： $△ A A^{'} C ∽ △ B B^{'} C$ ；

(2)、如图②，当 $α = 90 °$ 时，点 $A ′$ 在 $B C$ 上， $A A^{'}$ 的延长线交 $B B^{'}$ 于点P ，请确定 $A A^{'}$ 与 $B B^{'}$ 的位置关系，并说明理由；

(3)、如图③，当 $90 ° < α < 180 °$ 时，如果 $A^{'} C$ $∥ A B$ ，连接 $A^{'} B$ ，求 $A^{'} B$ 的长．

查看试题解析