贵州省黔东南州2023-2024学年七年级上学期数学期末考试试卷
试卷更新日期:2024-03-26 类型:期末考试
一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置作答,每题3分,共36分。
-
1. 2023的相反数是( )A、 B、 C、 D、2. 马拉松是国际上非常普及的长跑比赛项目,全程距离26英里385码,折合约为42000米,用科学记数法表示42000为A、 B、 C、 D、3. 如图,图中三角形绕虚线旋转一周,能围成的几何体是
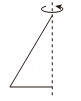 A、
A、 B、
B、 C、
C、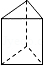 D、
D、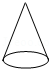 4. 单项式系数与次数分别是A、2,2 B、2,3 C、 , 3 D、 , 25. 若是关于的方程的解,则的值是A、 B、1 C、 D、36. 如图所示,能用∠AOB,∠O,∠1三种方法表示同一个角的图形的是( )A、
4. 单项式系数与次数分别是A、2,2 B、2,3 C、 , 3 D、 , 25. 若是关于的方程的解,则的值是A、 B、1 C、 D、36. 如图所示,能用∠AOB,∠O,∠1三种方法表示同一个角的图形的是( )A、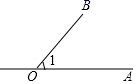 B、
B、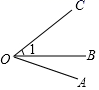 C、
C、 D、
D、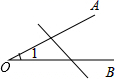 7. 如图,建筑工人砌墙时,经常在两个墙角的位置分别插一根木桩,然后拉一条直的参照线,其依据的基本事实是
7. 如图,建筑工人砌墙时,经常在两个墙角的位置分别插一根木桩,然后拉一条直的参照线,其依据的基本事实是 A、两点之间,线段最短 B、经过两点有一条直线 C、直线比线段长 D、两点确定一条直线8. 将矩形ABCD沿AE折叠,得到如图图形.若∠CED′=56°,则∠AED的大小是( )
A、两点之间,线段最短 B、经过两点有一条直线 C、直线比线段长 D、两点确定一条直线8. 将矩形ABCD沿AE折叠,得到如图图形.若∠CED′=56°,则∠AED的大小是( )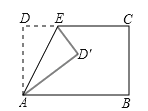 A、56° B、60° C、62° D、65°9. 下列方程的变形正确的是( ).A、由 移项,得 B、由 去括号,得 C、由 系数化为1,得 D、由 去分母,得10. 一个长方形的周长为 , 其中一边的长为 , 则另一边的长为A、 B、 C、 D、11. 《九章算术》是中国古代的一部数学专著,其中记载了一道有趣的题:“今有凫起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”大意是:今有野鸭从南海起飞,7天到北海;大雁从北海起飞,9天到南海.现野鸭从南海,大雁从北海同时起飞,问经过多少天相遇?设经过天相遇,根据题意可列方程为A、 B、 C、 D、12. 观察下列“蜂窝图”,按照这样的规律,则第2023个图案中的“”的个数是
A、56° B、60° C、62° D、65°9. 下列方程的变形正确的是( ).A、由 移项,得 B、由 去括号,得 C、由 系数化为1,得 D、由 去分母,得10. 一个长方形的周长为 , 其中一边的长为 , 则另一边的长为A、 B、 C、 D、11. 《九章算术》是中国古代的一部数学专著,其中记载了一道有趣的题:“今有凫起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”大意是:今有野鸭从南海起飞,7天到北海;大雁从北海起飞,9天到南海.现野鸭从南海,大雁从北海同时起飞,问经过多少天相遇?设经过天相遇,根据题意可列方程为A、 B、 C、 D、12. 观察下列“蜂窝图”,按照这样的规律,则第2023个图案中的“”的个数是
 A、6074 B、6072 C、6070 D、6068
A、6074 B、6072 C、6070 D、6068二、填空题:每小题4分,共16分
-
13. 计算:=14. 已知 , 则余角的度数是 .15. 若与是同类项,则的值为 .16. 如图,长方形中, , , 为的中点.动点从点出发,以每秒的速度沿运动,最终到达点 . 若点运动的时间为秒,则当时,的面积等于5.
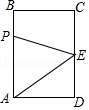
三、解答题:本大题9小题,共98分,解答应写出必要的文字说明、证明过程或者演推步骤。
-
17. 计算:(1)、;(2)、 .18.(1)、;(2)、 .19. 化简求值: , 其中 , .20. 已知四点 , , , (如图),根据下列要求,画出相应图形:
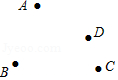 (1)、画直线;(2)、画射线、 , 交于点;(3)、连接、 , 相交于点 .21. 最近几年时间,全球的新能源汽车发展迅猛,尤其对于我国来说,新能源汽车产销量都大幅增加.小明家新换了一辆新能源纯电动汽车,他连续7天记录了每天行驶的路程(如表).每天以为标准,多于的记为“”,不足的记为“”
(1)、画直线;(2)、画射线、 , 交于点;(3)、连接、 , 相交于点 .21. 最近几年时间,全球的新能源汽车发展迅猛,尤其对于我国来说,新能源汽车产销量都大幅增加.小明家新换了一辆新能源纯电动汽车,他连续7天记录了每天行驶的路程(如表).每天以为标准,多于的记为“”,不足的记为“”第一天
第二天
第三天
第四天
第五天
第六天
第七天
路程
0
(1)、这7天里路程最多的一天比最少的一天多走 ;(2)、请求出小明家的新能源汽车这七天一共行驶了多少千米?(3)、已知汽油车每行驶大约需用汽油7升,汽油价为8元升:而新能源汽车每行驶耗电量大约为20度,每度电价为0.8元,请估计小明家换成新能源汽车后,这7天的行驶费用比原来节省多少钱?22. (1)、如图1,线段 , 线段 , 点是的中点,在上取一点 , 使得 , 求的长.(2)、如图2,为直线上一点, , 平分 , , 求的度数.23. 盲盒近来火爆,这种不确定的“盲抽”模式受到了年轻人的青睐,某商场计划采购潮玩盲盒和高品质精品盲盒,计划采购两种盲盒共500盒,这两种盲盒的进价、售价如下表:
(1)、如图1,线段 , 线段 , 点是的中点,在上取一点 , 使得 , 求的长.(2)、如图2,为直线上一点, , 平分 , , 求的度数.23. 盲盒近来火爆,这种不确定的“盲抽”模式受到了年轻人的青睐,某商场计划采购潮玩盲盒和高品质精品盲盒,计划采购两种盲盒共500盒,这两种盲盒的进价、售价如下表:类型
进价(元盒)
售价(元盒)
潮玩盲盒
20
25
高品质精品盲盒
68
88
(1)、若采购共用去14800元,则两种盲盒各采购了多少盒?(2)、在(1)的条件下全部售完这500盒,则商场能获利多少元?24. 如图是一个长方体的表面展开图,一共标有、、、、、六个面, , , , 请根据要求回答: (1)、与相对的面是 ;与相对的面是(2)、求这个长方体的表面积和体积(用含和的式子表示).25. 将一副直角三角尺按如图1摆放在直线上(直角三角尺和直角三角尺 , , , , , 保持三角尺不动,将三角尺绕点顺时针方向转动.当转动至射线上时,三角板停止转动.
(1)、与相对的面是 ;与相对的面是(2)、求这个长方体的表面积和体积(用含和的式子表示).25. 将一副直角三角尺按如图1摆放在直线上(直角三角尺和直角三角尺 , , , , , 保持三角尺不动,将三角尺绕点顺时针方向转动.当转动至射线上时,三角板停止转动. (1)、如图2,当平分时,度.(2)、三角尺转动到如图3的位置,使得、同时在直线的右侧,猜想与有怎样的数量关系?并说明理由.(3)、在三角尺转动的过程中,是否存在 , 若存在,求出的度数,若不存在,请说明理由.
(1)、如图2,当平分时,度.(2)、三角尺转动到如图3的位置,使得、同时在直线的右侧,猜想与有怎样的数量关系?并说明理由.(3)、在三角尺转动的过程中,是否存在 , 若存在,求出的度数,若不存在,请说明理由.