2023-2024学年湘教版初中数学七年级下学期 6.2 方差同步分层训练培优题
试卷更新日期：2024-03-26 类型：同步测试
一、选择题
-
1. 若数据1，2，3，4，5的方差是a，则数据7，8，9，10，11的方差是 （ ）A、a B、2a C、4a D、5a2. 甲、乙两人在相同的条件下，各射击10次，经计算：甲射击成绩的平均数是8环，方差是1.1环²，乙射击成绩的平均数是8环，方差是1.5环².下列说法中不一定正确的是（ ）A、甲、乙的总环数相同 B、甲的成绩比乙的成绩稳定 C、乙的成绩比甲的成绩波动大 D、甲、乙成绩的众数相同3. 为贯彻落实教育部办公厅关于“保障学生每天校内，校外各1小时体育活动时间”的要求，学校要求学生每天坚持体育锻炼.小亮记录了自己一周内每天校外锻炼的时间（分），并制作了如图所示的统计图.根据统计图，下列关于小亮该周每天校外锻炼时间的描述，正确的是（ ）
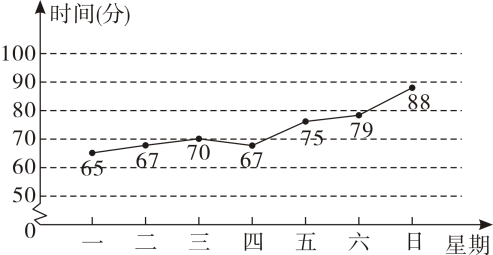A、平均数为70分钟 B、众数为67分钟 C、中位数为67分钟 D、方差为04. 为了解某小区居民的用水情况，随机抽查了若干户家庭的某月用水量，统计结果如下表所示：月用水量（吨）
3
4
5
6
户数
4
6
8
2
下列关于这若干户家庭的该月用水量的数据统计分析，说法正确的是 （ ）
A、众数是 2 吨 B、平均数是 4.5 吨 C、中位数是 5 吨 D、方差是0.84 吨²5. 甲、乙、丙、丁四个小组的同学分别参加了班里组织的中华古诗词知识竞赛，四个小组的平均分相同，若要从中选择出一个各成员实力更平均的小组参加年级的比赛，那么应选（ ）甲
乙
丙
丁
方差
3.6
3.2
4
4.3
A、甲组 B、乙组 C、丙组 D、丁组6. 小华进行了5次射击训练后，计算出这5次射击的平均成绩为8环，方差为s12 ， 随后小华又进行了第6次射击，成绩恰好是8环，并计算出这6次射击成绩的方差为s22 ， 则下列说法正确的是（ ）
A、s12=s22 B、s12＜s22 C、s12＞s22 D、无法确定s12与s22的大小7. 如果一组数据x1 ， x2 ， …，xn的方差是4，则另一组数据x1+3，x2+3，…，xn+3的方差是（ ）
A、4 B、7 C、8 D、198.在某次训练中，甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示，对于本次训练，有如下结论：①S甲2＞S乙2；②S甲2＜S乙2；③甲的射击成绩比乙稳定；④乙的射击成绩比甲稳定，由统计图可知正确的结论是（ ）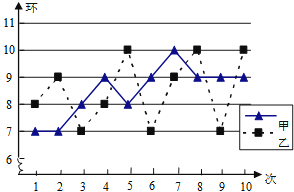
A、①③ B、①④ C、②③ D、②④二、填空题
-
9. 已知一组数据x₁，x₂，x₃，…，x。的方差是 1.5，则另一组 数 据 2x₁，2x₂， 2x₃，…，2x， 的方差是.10. 已知一组数据x1 ， x2 ， x3 ， x4 ， x5等的平均数是2，方差是1 ，则数据3x1-2，3x2-2，3x3-2，3x4-2，3x5-2的平均数是 ， 方差是11. 有两个女生小合唱队，各由6名队员组成，甲队与乙队的平均身高均为160 cm，甲队身高方差=1.2 cm2 ， 乙队身高方差=2.0 cm2 ， 两队身高比较整齐的是队（填“甲”或“乙”）.12. 为迎接体育测试，小强每天坚持引体向上锻炼，他记录了某一周每天做引体向上的个数，如下表：
其中有三天的个数被墨汁覆盖了，但小强已经计算出这组数据唯一的众数是13，平均数是12，那么这组数据的方差是。
13. 如果一组按从小到大排序的数据a，b，c的平均数是b，方差是S2 ， 那么数据a+99，b+100，c+101的方差将 S2（填“大于”“小于”或“等于”）.三、解答题
-
14. 体育老师要从每班选取一名同学参加学校的跳绳比赛，小静和小炳是跳绳能手，下面分别是小静、小炳 6次跳绳成绩的统计图和成绩分析表.
小静、小炳6次跳绳成绩的折线统计图
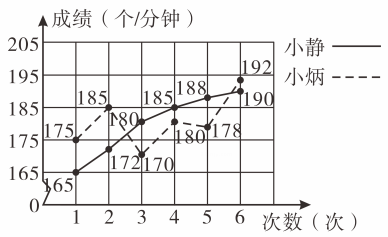
小静、小炳6次跳绳成绩分析表
成绩学生
平均数
中位数
方差
小静
180
182.5
79.7
小炳
180
a
49.7
(1)、根据统计图中的数据，表中 a=.(2)、结合以上信息，请你从两个不同的角度评价这两位学生的跳绳水平。15. 甲、乙两名队员参加射击训练，每人射击10次，成绩分别如下：根据以上信息，整理分析数据如下：
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)、 ， ， .(2)、填空：（填“甲”或“乙”）.从中位数的角度来比较，成绩较好的是；从众数的角度来比较，成绩较好的是；成绩相对较稳定的是.
(3)、从甲、乙两名队员中选一名队员参加比赛，选谁更合适，为什么？四、综合题
-
16. 为了了解甲、乙、丙三种型号的扫地机器人的扫地质量，工作人员从某月生产的甲、乙、丙三种型号扫地机器人中各随机抽取10台，在完全相同条件下试验，记录下它们的除尘指数的数据，并进行整理、描述和分析，下面给出了部分信息．
ⅰ.甲、乙两种型号扫地机器人除尘指数的折线图：
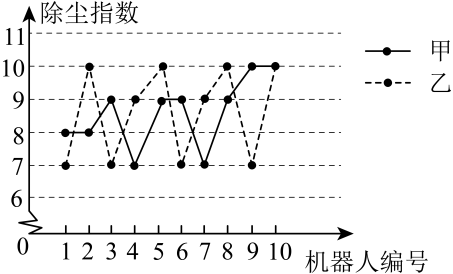
ⅱ.丙型号扫地机器人的除尘指数数据：10，10，10，9，9，8，3，9，8，10.
ⅲ．甲、乙、丙三种型号机器人除尘指数的平均数：
扫地机器人
甲
乙
丙
除尘指数平均数
8.6
8.6
m
根据以上信息，回答下列问题：
(1)、求表中m的值；(2)、在抽取的扫地机器人中，如果除尘指数的10个数据的方差越小，则认为该型号的扫地机器人性能更稳定．据此推断：在甲、乙两种型号扫地机器人中，型扫地机器人的性能稳定（填“甲”或“乙”）；(3)、在抽取的扫地机器人中，如果把10个除尘指数去掉一个最高值和一个最低值之后的平均值作为性能参考，平均值越高，则认为该型号扫地机器人性能表现越优秀．据此推断：在甲、乙、丙三种型号的扫地机器人中，表现最优秀的是（填“甲”、“乙”或“丙”）．17. 2023年3月5日，中华人民共和国第十四届全国人民代表大会第一次会议在北京召开，某校为使学生更好地了解“两会”，争做新时代好少年，开展了“两会”知识竞赛活动，分别从八（1）班和八（2）班各随机抽取10名学生的竞赛成绩（单位：分，满分100分），并对数据进行了如下分析与整理：收集数据
八（1）班学生知识竞赛成绩：84，75，82，70，91，83，80，74，79，82
八（2）班学生知识竞赛成绩：80，65，75，68，95，82，84，80，92，79
分析数据
平均数/分
中位数/分
众数/分
方差
八（1）班
80
b
82
31.6
八（2）班
a
80
c
78.4
根据以上信息，解答下列问题：
(1)、填空： ， ， ．(2)、请你对八（1）班和八（2）班抽取的这10名学生的知识竞赛成绩作出评价．(3)、该校除开展两会知识竞赛活动外，还组织了制作关于“两会”手抄报的评比活动，并对手抄报进行评分（单位：分，满分100分）．在八（2）班抽取的这10名学生中，甲同学和乙同学的知识竞赛成绩分别为95分和92分，手抄报成绩分别为70分和80分．现对甲同学和乙同学进行综合评分，若知识竞赛成绩占70%，手抄报成绩占30%，则哪位同学的综合成绩较好？