2023-2024学年湘教版初中数学七年级下学期 6.2 方差同步分层训练基础题

试卷更新日期：2024-03-26 类型：同步测试

进入出卷网下载

一、选择题

1. 甲、乙两名射击运动员分别进行了相同次数的射击训练，如果将甲、乙两人射击环数的平均数分别记作 ${\bar{x}}_{甲}$ 和 ${\bar{x}}_{乙}$ ，方差分别记作 $S_{甲}^{2}$ 和 $S_{乙}^{2}$ ，那么下列描述能说明甲运动员成绩较好且更稳定的是（）

A、 ${\bar{x}}_{甲} > {\bar{x}}_{乙}$ 且 $S_{甲}^{2} < S_{乙}^{2}$ B、 ${\bar{x}}_{甲} > {\bar{x}}_{乙}$ 且 $S_{甲}^{2} > S_{乙}^{2}$ C、 ${\bar{x}}_{甲} < {\bar{x}}_{乙}$ 且 $S_{甲}^{2} < S_{乙}^{2}$ D、 ${\bar{x}}_{甲} < {\bar{x}}_{乙}$ 且 $S_{甲}^{2} > S_{乙}^{2}$

查看试题解析
2. 南山区博物馆五位小讲解员的年龄分别为10，12，12，13，15（单位：岁），则三年后这五位小讲解员的年龄数据中一定不会改变的是（）

A、方差 B、众数 C、中位数 D、平均数

查看试题解析
3. 如下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差．根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（）

甲
乙
丙
丁
平均（ $c m$ ）
$165$
$160$
$165$
$160$
方差
$2.5$
$2.5$
$6.4$
$7.1$

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 为贯彻落实教育部办公厅关于“保障学生每天校内，校外各1小时体育活动时间”的要求，学校要求学生每天坚持体育锻炼.小亮记录了自己一周内每天校外锻炼的时间（单位：分钟），并制作了如图所示的统计图.根据统计图，下列关于小亮该周每天校外锻炼时间的描述，正确的是（）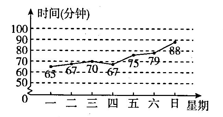

A、平均数为70分钟 B、众数为67分钟 C、中位数为67分钟 D、方差为30分钟2

查看试题解析
5. 某创意工作室6位员工的月基本工资如图所示，因业务发展需要，现决定招聘一名新员工.若新员工的月基本工资为 4 500元，则下列关于现在7位员工的月基本工资的平均数和方差的说法中，正确的是（）
某创意工作室6位员工的月基本工资折线统计图

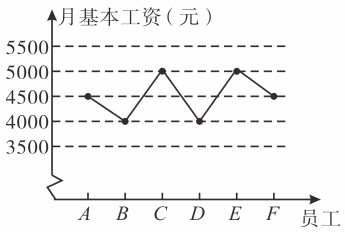A、平均数不变，方差变大 B、平均数不变，方差变小 C、平均数不变，方差不变 D、平均数变小，方差不变

查看试题解析
6. 某地积极号召居民节约用水，为了解居民用水情况，在一个小区随机抽查了10户家庭的月用水量，将统计结果绘制为如图所示的条形统计图，则下列关于这10户家庭的月用水量(单位：吨)的说法正确的是（）
某小区10户家庭的月用水量条形统计图

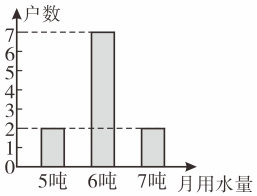A、众数是5吨 B、中位数是 6吨 C、平均数是7吨 D、方差是 8 吨²

查看试题解析
7. 甲、乙两人在相同条件下，各射击10次，经计算，甲射击成绩的平均数是8环，方差是 $1.2$ $环^{2}$ ；乙射击成绩的平均数是8环，方差是 $1.6$ $环^{2}$ ．下列说法不一定正确的是（）

A、甲、乙成绩的总环数相同 B、甲的成绩比乙的成绩稳定 C、甲、乙成绩的中位数可能相同 D、甲、乙成绩的众数一定相同

查看试题解析
8. 如图是根据某店今年6月 1日至5日每天的用水量(单位：吨)绘制成的折线统计图.下列结论正确的是（）

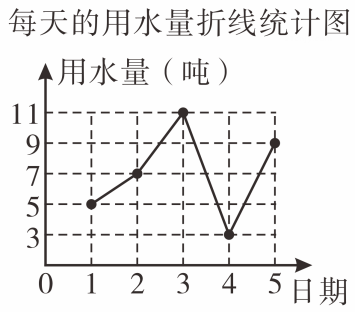A、平均数是6 B、众数是7 C、中位数是 11 D、方差是8

查看试题解析

二、填空题

9. 小云和小天练习射击，一轮10发子弹打完后，两人的成绩如图所示.根据图中的信息，小云和小天两人中成绩较稳定的是.

查看试题解析
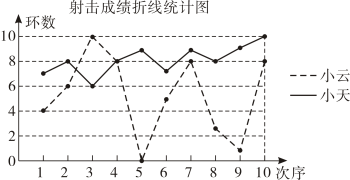10. 跳高训练时，甲、乙两名同学在相同条件下各跳了 $10$ 次，统计他们的平均成绩都是 $1.36$ 米，且方差为 $S_{甲}^{2} = 0.4$ ， $S_{乙}^{2} = 0.3$ ，则成绩较为稳定的是 $($ 填“甲”或“乙” $)$ ．

查看试题解析
11. 在一次广场舞比赛中，甲、乙两个队参加表演的队员的身高(单位：cm)分别是：
甲队：163 165 165 164 168
乙队：162 164 164 167 168
甲队队员身高的方差为cm²，(填“甲”或“乙”)队队员的身高更整齐.

查看试题解析
12. 为了解“睡眠管理”落实情况，某校随机调查了46名学生每天平均睡眠时间，并将样本数据绘制成如图所示的统计图(其中有两个数据被遮盖).有以下关于睡眠时间的统计量：①平均数，②中位数，③众数，④方差，其中与被遮盖的数据无关的是(填序号).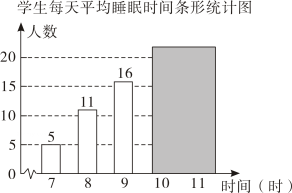

查看试题解析
13. 甲、乙两班举行数学知识竞赛，参赛学生的竞赛得分统计分析结果如下表所示：
班级
参赛人数
平均数(分)
中位数(分)
方差(分²)
甲
45
83
86
82
乙
45
83
84
135
某同学分析上表后得到如下结论：
①甲、乙两班学生的平均成绩相同；
②乙班优秀的人数少于甲班优秀的人数(竞赛得分≥85分为优秀)；
③甲班成绩比乙班稳定.
上述结论中，正确的是(填序号).

查看试题解析

三、解答题

14. 南明区某学校七、八年级举行“一二 $\cdot$ 九”演讲比赛，根据初赛成绩各选出了 $5$ 名选手 $($ 编号分别为 $1$ 、 $2$ 、 $3$ 、 $4$ 、 $5)$ 组成七年级代表队、八年级代表队参加学校决赛，根据这 $10$ 名选手的决赛成绩 $($ 满分为 $100$ 分 $)$ ，制作了如下的统计图表：
二
平均数
中位数
众数
方差
七年级
$85$
$85$
$m$
$70$
八年级

$80$
$100$

(1)、表格中 $m =$ ；

(2)、请求出八年级代表队参加学校决赛的平均成绩；

(3)、要从这两个年级代表队中选出一个年级，代表学校去参加南明区的比赛，你认为应该选择哪个年级代表队？请说明理由．

查看试题解析
15. 某校拟派一名跳高运动员参加一项校际比赛，对甲、乙两名跳高运动员进行了8次选拔比赛，他们的成绩（单位： $m$ ）如下：
甲： 1. 71，1. 65，1. 68，1. 68，1. 72，1. 73，1. 68，1. 67；
乙： 1. 60，1. 74，1. 72，1. 69，1. 62，1. 71，1. 69，1. 75；

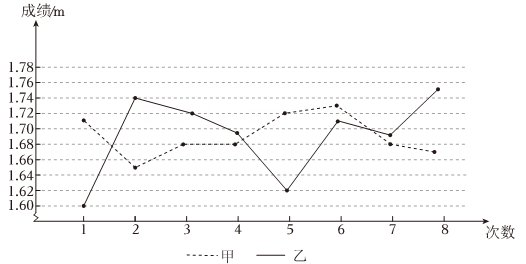(1)、【整理与分析】
平均数众数中位数
甲 1.69 a 1.68
乙 1.69 1.69 b

①由上表填空： $a =$ ， $b =$ ；
②这两人中，的成绩更为稳定。

(2)、【判断与决案】
经预测，跳高 $1.69 m$ 就很可能获得冠军，该校为了获取跳高比赛冠军，可能选哪位运动员参赛？请说明理由。

查看试题解析

四、综合题

16. 为了解甲、乙两个班在数学测试中对某一个解答题的解答情况，分别在两个班随机抽取了20名学生的成绩（满分10分），对其进行整理、描述和分析．下面给出①、②两组信息：

①乙班20名学生成绩的条形统计图如图所示：

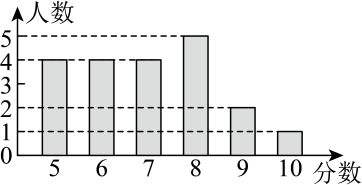
②甲、乙两个班所抽取的20名学生成绩的平均数、众数、中位数和方差如下表所示：（单位：分）

班级	平均数	众数	中位数	方差
甲	7	7	7	$S_{甲}^{2} = 2.15$
乙	7	m	p	$S_{乙}^{2}$

根据以上信息，解答下列问题：

(1)、填空：上表中

m =

，

p =

；

(2)、求上表中

S_{乙}^{2}

的值，并用样本估计总体的方法分析哪个班学生的成绩表现更稳定？

查看试题解析

17. 某校为了了解本校学生对航天科技的关注程度，对八、九年级学生进行了航天科普知识竞赛（百分制），并从其中分别随机抽取了20名学生的测试成绩，整理、描述和分析如下：（成绩得分用 $x$ 表示，共分成四组： $A . 80 ⩽ x < 85 ； B . 85 ⩽ x < 90 ； C . 90 ⩽ x <$ $95 ； D . 95 ⩽ x ⩽ 100)$
其中，八年级20名学生的成绩是：80，81，82，82，84，85，86，87，89，90，90，91，94，96，96，96，96，96，99，100.
九年级20名学生的成绩在 $C$ 组中的数据是：90，91，92，92，93，94.
八、九年级抽取的学生竞赛成绩统计表
年级
平均数
中位数
众数
方差
八年级
90
90
b
38.7
九年级
90
c
100
38.1
根据以上信息，解答下列问题：

(1)、直接写出上述a、b、c的值： $a =$ ， $b =$ ， $c =$ ；

(2)、你认为这次比赛中哪个年级的竞赛成绩更好，为什么?

(3)、若该校九年级共1400人参加了此次航天科普知识竞赛活动，估计参加此次活动成绩优秀 $(x ⩾ 90)$ 的九年级学生人数.

查看试题解析

	甲	乙	丙	丁
平均（ $c m$ ）	$165$	$160$	$165$	$160$
方差	$2.5$	$2.5$	$6.4$	$7.1$

班级	参赛人数	平均数(分)	中位数(分)	方差(分²)
甲	45	83	86	82
乙	45	83	84	135

年级	平均数	中位数	众数	方差
八年级	90	90	b	38.7
九年级	90	c	100	38.1

二	平均数	中位数	众数	方差
七年级	$85$	$85$	$m$	$70$
八年级		$80$	$100$