2023-2024学年湘教版初中数学七年级下学期 6.1.3 众数同步分层训练提升题

试卷更新日期：2024-03-26 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 某篮球队10名队员的年龄如下表所示：

    年龄(岁)

    18

    19

    20

    21

    人数

    2

    4

    3

    1

    这10名队员年龄的众数(单位：岁)和中位数(单位：岁)分别是（ ）

    A、19，19 B、19，19.5 C、20，19 D、20，19.5

    查看试题解析

  • 2. 学校气象社的同学们对当地的日最高气温进行了连续14 天的测量，统计结果(精确到个位)如下表：

    日最高气温(℃)

    16

    18

    19

    20

    21

    天数

    3

    3

    4

    2

    2

    这14天中，当地日最高气温的众数和中位数分别为 （ ）

    A、19 ℃，18 ℃ B、19℃，19 ℃ C、21 ℃，18 ℃ D、21℃，19 ℃

    查看试题解析

  • 3. 为了解某小区“全民健身”活动的开展情况，随机对居住在该小区的40名居民一周的体育锻炼时间进行了统计，结果如表：

    锻炼时间（时）

    3

    4

    5

    6

    7

    人数（人）

    6

    13

    14

    5

    2

    这40名居民一周体育锻炼时间的众数和中位数是（ ）

    A、14，5 B、5，5 C、14，6 D、5，6

    查看试题解析

  • 4. 下列表格列举了 2022年卡塔尔世界杯优秀球员的射门次数，观察表格中的数据，这组数据的中位数和众数分别是 （ ）

    球员

    梅西

    姆巴佩

    佩里西奇

    吉鲁

    马丁内斯

    奥尔莫

    射门次数

    32

    31

    16

    16

    14

    12

    A、32，16 B、16，31 C、16，16 D、16，14

    查看试题解析

  • 5. 如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况(满分5 分)，则所打分数的众数为（ ）

    课后延时服务的打分情况扇形统计图

    A、5分 B、4分 C、3分 D、45%

    查看试题解析

  • 6. 抽查某班10名同学的中考体育测试成绩如下表所示：

    成绩(分)

    30

    25

    20

    15

    人数

    2

    x

    y

    1

    若成绩的平均数是 23，中位数是 a，众数是b，则a -b的值为 （ ）

    A、-5 B、-2.5 C、2.5 D、5

    查看试题解析

  • 7. 如图是根据某地某段时间的每天最低气温绘成的折线图，那么这段时间最低气温的中位数、众数、平均数依次是（ ）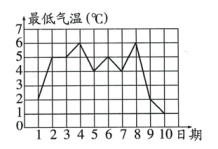

    A、4℃，5℃，4℃ B、5℃，5℃，4.5℃ C、4.5℃，5℃，4℃ D、4.5℃，5℃，4.5℃

    查看试题解析

  • 8. 为贯彻落实教育部《关于全面加强新时代大中小学劳动教育的意见》，把劳动教育纳入人才培养全过程，某校组织学生周末赴劳动教育实践基地开展锄地、除草、剪枝、捉鱼、采摘五项实践活动，已知五个项目参与的人数分别是：35，38，39，42，42，则这组数据的众数和中位数分别是（ ）
    A、38，39 B、35，38 C、42，39 D、42，35

    查看试题解析

二、填空题

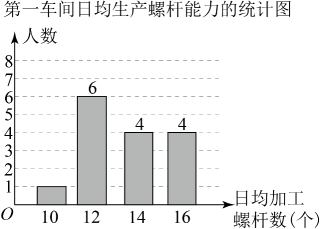
  • 9. 两组数据：3 ， x ， 2y ， 5与x ， 6 ， y的平均数都是6 ， 若将这两组数据合并为一组新数据：3 ， x ， 2y ， 5 ， x ， 6 ， y ， 则这组新数据的众数为 ．

    查看试题解析

  • 10. 若一组数据x，3，1，6，3的平均数和众数相等，则x的值为

    查看试题解析

  • 11. 某工厂第一车间有15名工人，每人日均加工螺杆数统计如图．则该车间工人日均生产螺杆数的中位数是个，众数是个．

    查看试题解析

  • 12. 我市体育中考有必考和选考项目，掷实心球是必考项目之一，在一次训练中，张华同学掷实心球10次的成绩依次是（单位：米）7.6，8.5，8.6，8.5，9.1，8.5，8.4，8.6，9.2，73．则张华同学撰实心球成绩的众数是 ．

    查看试题解析

  • 13. 为了解学生的睡眠状况，调查了一个班50名学生每天的睡眠时间，绘成睡眠时间条形统计图（如图所示），则所调查学生睡眠时间的众数和中位数分别为和 ．

    查看试题解析

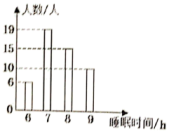
三、解答题

  • 14. 某校落实“双减”政策，提倡课内高效学习，把课外时间归还学生.“鸿志”班为了激发学生学习热情，提高学习成绩，采用分组学习方案，每7 人为一小组，经过半个学期的学习，在模拟测试中，某小组7人的成绩(单位：分)分别为 98，94，92，88，95，98，100.
    (1)、该小组学生成绩的中位数是 ， 众数是. 
    (2)、若成绩95分及以上评为优秀，求该小组成员成绩的平均分和优秀率(百分率保留整数).

    查看试题解析

  • 15. 某中学八年级组织了一次数学计算竞赛，每班选25名同学参加竞赛，成绩分为 A，B，C，D 四个等级，其中A等级得分为100分，B等级得分为90分，C等级得分为80分，D等级得分为 70分.数学教研组将八年级一班和二班的成绩整理并绘制成如图的统计图，请根据图中信息解答下列问题.

    一班竞赛成绩条形统计图 二班竞赛成绩扇形统计图

    (1)、把一班竞赛成绩条形统计图补充完整。
    (2)、求出下表中a，b，c的值.

    平均数(分)

    中位数(分)

    众数(分)

    一班

    a

    b

    90

    二班

    87.6

    80

    C

    (3)、请从以下给出的两个方面对这次竞赛成绩的结果进行分析：

    ①从平均数、众数两方面来比较一班和二班的成绩.

    ②从B级及以上的人数来比较一班和二班的成绩.

    查看试题解析

四、综合题

  • 16. 甲、乙两位同学参加数学质量测试活动，各项成绩如下（单位：分）

     

    数与代数

    空间与图形

    统计与概率

    综合与实践

    学生甲

             90

             93

             89

             90

    学生乙

             94

             92

             94

             86
    (1)、学生甲成绩的中位数是 ， 学生乙成绩的众数是；
    (2)、如果将“数与代数”“ 空间与图形”“ 统计与概率”“ 综合与实践”四项成绩按3：3：2：2的比例确定最终成绩，通过计算说明学生甲、乙谁的成绩较高．

    查看试题解析

  • 17. 为了加强对青少年防溺水安全教育，4月初某校开展了“远离溺水，珍爱生命”的防溺水安全知识比赛．下面是从参赛学生中随机收集到的20名学生的成绩（单位：分）：

    87  99  86  89  91  91  95  96  87  97

    91  97  96  86  96  89  100  91  99  97

    整理数据：

    成绩（分）

    86

    87

    89

    91

    95

    96

    97

    99

    100

    学生人数（人）

    2

    2

    2

    4

    1

    3

    3

    2

    1

    分析数据：

    平均数

    众数

    中位数

    93

    a

    b

    解决问题：

    (1)、直接写出：上面表格中的a= ， b=；
    (2)、若成绩达到95分及以上为“优秀”等级，求“优秀”等级所占的百分率为；
    (3)、请估计该校1500名学生中成绩达到95分及以上的学生人数．

    查看试题解析