2023-2024学年湘教版初中数学七年级下学期 6.1.1 平均数同步分层训练培优题

试卷更新日期：2024-03-26 类型：同步测试

进入出卷网下载

一、选择题

1. 已知一组数据 x₁，x₂，x₃ 的平均数是7，则 $x_{1}$ $+ 3 ， x_{2} + 2 ， x_{3} + 4$ 的平均数是（）

A、7 B、8 C、9 D、10

查看试题解析
2. 骐骥中学规定，学生的学期体育成绩满分为100，其中体育课外活动占20%，期中考试成绩占30%，期末考试成绩占50%．若嘉淇同学的三项成绩（百分制）依次是96分，92分，97分，则嘉淇这学期的体育成绩是（）

A、95分 B、95.1分 C、95.2分 D、95.3分

查看试题解析

3. 某公司要招聘一名职员，根据实际需要，从学历、经验和工作态度三方面对甲、乙、丙三名应聘者进行了测试，测试成绩如表所示：如果将学历、经验和工作态度三项得分按

1

：

1

：

2

的比例确定三人的最终得分，并以此为依据录用得分最高者，那么被录用的是（）

应聘者	学历	经验	工作态度
甲	$9$	$8$	$5$
乙	$8$	$6$	$8$
丙	$9$	$7$	$6$

A、甲 B、乙 C、丙 D、不能确定

查看试题解析

4. 在凤凰山教育共同体数学学科节中，为展现数学的魅力，M老师组织了一个数学沉浸式互动游戏：随机请A ， B ， C ， D ， E五位同学依次围成一个圆圈，每个人心里先想好一个实数，并把这个数悄悄的告诉相邻的两个人，然后每个人把与自己相邻的两个人告诉自己的数的平均数报出来．若A ， B ， C ， D ， E五位同学报出来的数恰好分别是1，2，3，4，5，则D同学心里想的那个数是（）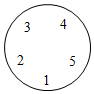

A、 $- 3$ B、 $- 4$ C、5 D、9

查看试题解析
5. 某校七年级举行大合唱比赛，六位评委给七年级一班的打分如下(单位：分)：9.20，9.40，9.60，9.50，9.80，9.50，则该班得分的平均分为（）

A、9.45分 B、9.50分 C、9.55分 D、9.60分

查看试题解析
6. 有甲、乙两种糖果，原价分别为每千克a元和b元，根据调查，将两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合，取得了较好的销售效果，现在糖果价格有了调整：甲种糖果单价下降15%，乙种糖果单价上涨20%，但按原比例混合的糖果单价恰好不变，则 $\frac{x}{y}$ =（）

A、 $\frac{3 a}{4 b}$ B、 $\frac{4 a}{3 b}$ C、 $\frac{3 b}{4 a}$ D、 $\frac{4 b}{3 a}$

查看试题解析
7. 根据下表中的信息解决问题：
数据
37
38
39
40
41
频数
8
4
5
a
1
若该组数据的中位数不大于38，则符合条件的正整数a的取值共有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
8. 某一公司共有51名员工（其中包括1名经理），经理的工资高于其他员工的工资，今年经理的工资从去年的200000元增加到225000元，而其他员工的工资同去年一样，这样，这家公司所有员工今年工资的平均数和中位数与去年相比将会（）

A、平均数增加，中位数不变 B、平均数和中位数不变 C、平均数不变，中位数增加 D、平均数和中位数均增加

查看试题解析

二、填空题

9. 某校拟招聘一批优秀教师，其中某位教师笔试、试讲、面试三轮测试的得分分别为89分、88分、92分，若综合成绩将笔试、试讲、面试按照2：3：4的比例计入，则该教师的综合成绩为分.

查看试题解析
10. 现有甲、乙两种糖果的单价与千克数如表所示．

甲种糖果
乙种糖果
单价(元/千克)
30
20
千克数
2
3
将这2千克甲种糖果和3千克乙种糖果混合成5千克什锦糖果，若商家用加权平均数来确定什锦糖果的单价，则这5千克什锦糖果的单价为元/千克.

查看试题解析
11. 某公司欲招聘一名职员，对甲、乙、丙三名应聘者进行了综合知识、工作经验、语言表达等三方面的测试，他们的各项成绩如下表所示：
综合知识工作经验语言表达
甲 75 80 80
乙 85 80 70
丙 70 78 70
如果将每位应聘者的综合知识、工作经验、语言表达的成绩按5∶2∶3的比例计算其总成绩，并录用总成绩最高的应聘者，那么被录用的是.

查看试题解析
12. 某学校九（1）班40名同学的期中测试成绩分别为 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ，……， $a_{40}$ .已知 $a_{1}$ + $a_{2}$ + $a_{3}$ +……+ $a_{40}$ = 4800，y= ${(a - a_{1})}^{2}$ + ${(a - a_{2})}^{2}$ + ${(a - a_{2})}^{2}$ +……+ ${(a - a_{40})}^{2}$ ，当y取最小值时，的值为.

查看试题解析
13. 已知：一组自然数1，2，3…k，去掉其中一个数后剩下的数的平均数为16，则去掉的数是．

查看试题解析

三、解答题

14. 某中学为加强学生的劳动教育，需要制定学生每周劳动时间(单位：时)的合格标准，为此随机调查了 100 名学生目前每周劳动时间，获得数据并整理成下表.
每周劳动时间x(时) 0.5≤x<1.5 1.5≤x<2.5 2.5≤x<3.5 3.5≤x<4.5 4.5≤x<5.5
组中值 1 2 3 4 5
人数 21 30 19 18 12

(1)、画扇形图描述数据时，1.5≤x<2.5这组数据对应的扇形的圆心角是多少度?

(2)、估计该校学生目前每周劳动时间的平均数.

(3)、请你为该校制定一个学生每周劳动时间的合格标准(时间取整数小时)，并用统计量说明其合理性.

查看试题解析
15. 小宇观看亚运会跳水比赛，对运动员每一跳成绩的计算方法产生了浓厚的兴趣，查阅资料后，小宇了解到跳水比赛的计分规则为：
(a)每次试跳的动作，按照其完成难度的不同，对应一个难度系数 H；
(b)每次试跳都有7 名裁判进行打分(0~10分，分数为0.5的整数倍)，在7个得分中去掉2个最高分和2个最低分，剩下 3个得分的平均值为这次试跳的完成分 P；
(c)运动员该次试跳的得分A=难度系数 H×完成分 P×3.
在比赛中，甲运动员最后一次试跳后的打分如下表所示：
难度系数
裁判
1#
2#
3#
4#
5#
6#
7#
3.5
打分
7.5
8.5
4.0
9.0
8.0
8.5
7.0

(1)、甲运动员这次试跳的完成分 P_甲= ，得分A_甲=.

(2)、如果按照全部7 名裁判打分的平均分来计算完成分，得到的完成分为 P_甲'，那么与(1)中所得的P_甲比较， P_甲'P_甲(填“>”“<”或 “= ”).

(3)、在最后一次试跳之前，乙运动员的总分比甲运动员低13.1分，已知乙最后一次试跳的难度系数为3.6，若乙想要在总分上反超甲，则这一跳乙的完成分 P_乙至少要达到多少分?

查看试题解析

四、综合题

16. 已知5个数a₁ ， a₂ ， a₃ ， a₄ ， a₅的平均数为m，则

(1)、a₁ ， a₂ ， a₃ ， 0，a₄ ， a₅ ，这6个数的平均数为；

(2)、2a₁ ， 2a₂ ， 2a₃ ， 2a_4，2a₅这5个数的平均数为；

(3)、若5个数b₁ ， b₂ ， b₃ ， b₄ ， b₅的平均数为n，则2a₁+b₁ ， 2a₂+b₂ ， 2a₃+b₃ ， 2a₄+b₄ ， 2a₅+b₅这5个数的平均数为。

查看试题解析
17. 某种水彩笔，在购买时，若同时额外购买笔芯，每个优惠价为3元，使用期间，若备用笔芯不足时需另外购买，每个5元．现要对在购买水彩笔时应同时购买几个笔芯作出选择，为此收集了这种水彩笔在使用期内需要更换笔芯个数的30组数据．

水笔支数

4

6

8

7

5

需要更换的笔芯个数x

7

8

9

10

11

设x表示水彩笔在使用期内需要更换的笔芯个数，y表示每支水彩笔在购买笔芯上所需要的费用（单位：元），n表示购买水彩笔的同时购买的笔芯个数．

(1)、若x＝9，n＝7，则y＝；若x＝7，n＝9，则y＝；

(2)、若n＝9，用含x的的代数式表示y的取值；

(3)、假设这30支笔在购买时，每支笔同时购买9个笔芯，或每支笔同时购买10个笔芯，分别计算这30支笔在购买笔芯时所需的费用，以费用最省作为选择依据，判断购买一支水彩笔的同时应购买9个还是10个笔芯？

查看试题解析

	综合知识	工作经验	语言表达
甲	75	80	80
乙	85	80	70
丙	70	78	70

每周劳动时间x(时)	0.5≤x<1.5	1.5≤x<2.5	2.5≤x<3.5	3.5≤x<4.5	4.5≤x<5.5
组中值	1	2	3	4	5
人数	21	30	19	18	12

难度系数	裁判	1#	2#	3#	4#	5#	6#	7#
3.5	打分	7.5	8.5	4.0	9.0	8.0	8.5	7.0

数据	37	38	39	40	41
频数	8	4	5	a	1

	甲种糖果	乙种糖果
单价(元/千克)	30	20
千克数	2	3

水笔支数	4	6	8	7	5
需要更换的笔芯个数x	7	8	9	10	11