2023-2024学年湘教版初中数学七年级下学期 6.1.1 平均数同步分层训练提升题

试卷更新日期：2024-03-26 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 样本数据2、a、3、4的平均数是3，则a的值是(　　)
    A、1 B、2 C、3 D、4

    查看试题解析

  • 2. 小明、小刚、小桐和小凯比赛谁投球比较远，每人投3次，结果如图所示．这四名同学中，（ ）投球的平均成绩大约是8米．

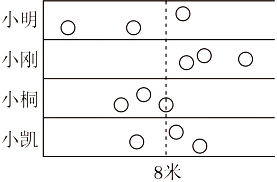    A、小明 B、小刚 C、小桐 D、小凯

    查看试题解析

  • 3. 在学校举办的合唱比赛中，八（3）班的演唱质量、精神风貌、配合默契得分分别为92分，80分，70分，若最终成绩由这三项得分依次按照 40% ， 30% ， 30%的百分比确定，则八（3）班的最终成绩是 （ ）
    A、80.6分 B、81.8分 C、84.7分 D、96.8分

    查看试题解析

  • 4. 已知数据x₁，x₂，⋯，xn的平均数是2，则 3x₁-2，3x₂-2，…，3x，-2的平均数是 （ ）
    A、0 B、2 C、4 D、6

    查看试题解析

  • 5. 某校进行广播操比赛，如图是20位评委给某班的评分情况统计图，则该班平均得分是（ ）

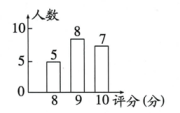    A、9分 B、6.67分 C、9.1分 D、6.74分

    查看试题解析

  • 6. 燕燕超市决定招聘广告策划人员一名，某应聘者三项素质测试的成绩如表：将创新能力、综合知识和语言表达三项测试成绩按5：3：2的比值计入总成绩，则该应聘者的总成绩是（　　）分．

    测试项目

    创新能力

    综合知识

    语言表达

    测试成绩（分数）

    70

    80

    92

    A、77.4 B、80.4 C、92 D、以上都不对

    查看试题解析

  • 7. 某住宅小区6月1日～6月5日每天用水量情况如图所示，那么这5天平均每天的用水量是（　　）

    A、25立方米 B、30立方米 C、32立方米 D、35立方米

    查看试题解析

  • 8. 现有12块完全相同的巧克力，每块至多被分为两小块，如果这12块巧克力可以平均分给n名同学，则n不可以为（ ）
    A、20 B、18 C、15 D、14

    查看试题解析

二、填空题

  • 9. 4月 23日是世界读书日，某校当天举行了演讲大赛，演讲得分按“演讲内容”占 40%，“语言表达”占40%，“形象风度”占 10%，“整体效果”占 10%进行计算，小芳这四项的得分依次为85，88，92，90，则她的最后得分是分.

    查看试题解析

  • 10. 甲、乙两位同学上学期有5 次数学检测，成绩如下表所示：

     

    第1次

    第2次

    第3次

    第4次

    第5次

    甲

    103分

    102分

    104分

    105分

    106分

    乙

    100分

    107分

    102分

    106分

    105 分

    (1)、甲、乙两位同学这五次数学检测成绩的平均分分别为.
    (2)、若前 3次为平时单元考成绩，第 4次为期中考成绩，第 5 次为期末考成绩.规定：平时单元考成绩的平均分占 30%，期中考成绩占20%，期末考成绩占 50%来计算总评成绩，甲、乙两位同学的学期总评成绩更好的是（填“甲”或“乙”）.

    查看试题解析

  • 11. 某公司决定招聘一名职员，一位应聘者三项素质测试的成绩如下表：

    测试项目

    创新能力

    专业知识

    语言表达

    测试成绩（分）

    70

    80

    92

    这三项成绩按照如图所示的比例确定综合成绩，则该应聘者最后的得分为分．

    查看试题解析

  • 12. 为了提高大家的环境保护意识，某小区在假期开展了废旧电池回收的志愿者活动，该小区有10名中学生参加了此项活动，他们回收的旧电池数量如下表：根据表中的数据，这10名中学生收集废旧电池的平均数为节.

    电池数量(节)

    2

    5

    6

    8

    10

    人数

    1

    4

    2

    2

    1

    查看试题解析

  • 13. 某校中学生开展社会实践活动，同学们在某小区随机调查了部分家庭一周内使用环保方便袋的数量，整理后制作了如图所示的统计图，请你根据统计图估计该小区每户一周内使用环保方便袋 个.

    查看试题解析

三、解答题

  • 14. 某公司要在甲、乙两人中招聘一名职员，对两人的学历、能力、经验这三项进行了测试.各项满分均为10分，成绩高者被录用，图1是甲、乙测试成绩的条形统计图·
    (1)、分别求出甲、乙三项成绩之和，并指出会录用谁.
    (2)、将甲、乙的三项测试成绩按照扇形统计图(如图2)各项所占之比，分别计算各自的综合成绩，并判断是否会改变(1)的录用结果

    查看试题解析

  • 15. 某校组织了一次“校徽设计”竞赛活动，邀请5名老师作为专业评委，50名学生代表参与民主测评，且民主测评的结果无弃权票，某作品的评比数据统计如下：
    专业评委给分（单位：分）
    ①88
    ②87
    ③94
    ④91
    ⑤90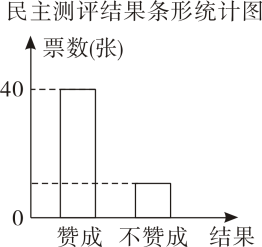

    (1)、求该作品在民主测评中得到“不赞成”的票数.
    (2)、记“专业评委给分”的平均数为x-.对于该作品，x-的值是多少?
    (3)、记“民主测评得分”为y- ， “综合得分”为S，若规定：

    ①y-=“赞成”的票数×3分+“不赞成”的票数×(-1)分；

    ②S=0.7x-+0.3y-.

    求该作品的“综合得分”S的值.

    查看试题解析

四、综合题

  • 16. 某班欲从甲、乙两名同学中推出一名同学，参加学校组织的数学素质测试竞赛，首先在班内对甲、乙两名同学进行了数与代数、图形与几何、统计与概率、综合与实践的测试，他们的各项成绩（百分制）如下表所示：

    学生

    数与代数

    图形与几何

    统计与概率

    综合与实践

    甲

    85

    89

    92

    94

    乙

    94

    92

    85

    80

    (1)、如果各项成绩同等重要，计算甲、乙两名同学的平均成绩，从他们的成绩看，应该推选谁？
    (2)、若数与代数、图形与几何、统计与概率、综合与实践的成绩按4：3：2：1的比确定，计算甲、乙两名同学的平均成绩，从他们的成绩看，应该推选谁？

    查看试题解析

  • 17. 为深入学习贯彻习近平法治思想，推动青少年宪法学习宣传教育走深走实，某校开展了宪法知识在线学习、知识竞赛与演讲比赛三项活动，下表是参加冠亚军决赛的两名选手的各项测试成绩（单位：分）．                                                                                                                                      

    选手/项目

    在线学习

    知识竞赛

    演讲比赛

    甲

    84

    96

    90

    乙

    89

    99

    85

    (1)、若将在线学习、知识竞赛与演讲比赛三项成绩的平均分作为最后成组，谁将获得冠军？
    (2)、若将在线学习、知识竞赛与演讲比赛的成绩按2：3：5的比例计算最后成绩，谁将获得冠军？

    查看试题解析