2023-2024学年湘教版初中数学七年级下学期 5.3 图形变换的简单应用同步分层训练提升题
试卷更新日期:2024-03-26 类型:同步测试
一、选择题
-
1. 下列图案中,不能由一个图形通过旋转而形成的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列大学校微可以看成是由图案自身的一部分经平移后得到的为( )A、
2. 下列大学校微可以看成是由图案自身的一部分经平移后得到的为( )A、 B、
B、 C、
C、 D、
D、 3. 如图,由图案(1)到图案(2)再到图案(3)的变化过程中,不可能用到的图形变换是( )
3. 如图,由图案(1)到图案(2)再到图案(3)的变化过程中,不可能用到的图形变换是( )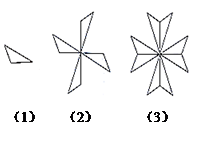 A、轴对称 B、旋转 C、中心对称 D、平移4. 甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,能用其中一部分平移得到的是( )A、
A、轴对称 B、旋转 C、中心对称 D、平移4. 甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,能用其中一部分平移得到的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,在 的正方形网格中两个小正方形被涂黑,再将图中其余小正方形任意一个涂黑,使得整个图形(包括网格)构成一个轴对称图形,那么涂法共有( )
5. 如图,在 的正方形网格中两个小正方形被涂黑,再将图中其余小正方形任意一个涂黑,使得整个图形(包括网格)构成一个轴对称图形,那么涂法共有( ) A、4种 B、5种 C、6种 D、7种6. 下面四个图案中,不能由基本图案(图中阴影部分)旋转得到的是( )A、
A、4种 B、5种 C、6种 D、7种6. 下面四个图案中,不能由基本图案(图中阴影部分)旋转得到的是( )A、 B、
B、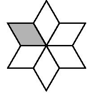 C、
C、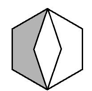 D、
D、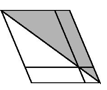 7. 如图是由三把相同大小的扇子展开后组成的图形,若把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”( )
7. 如图是由三把相同大小的扇子展开后组成的图形,若把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”( )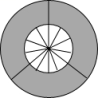 A、平移一次形成的 B、平移两次形成的 C、以轴心为旋转中心,旋转后形成的 D、以轴心为旋转中心,旋转、后形成的8. 如图,在 的正方形网格中,有5个小正方形已被涂黑(图中阴影部分),若在其余网格中再涂黑一个小正方形,使它与5个已被涂黑的小正方形组成的新图形是一个轴对称图形,则可涂黑的小正方形共有( )个.
A、平移一次形成的 B、平移两次形成的 C、以轴心为旋转中心,旋转后形成的 D、以轴心为旋转中心,旋转、后形成的8. 如图,在 的正方形网格中,有5个小正方形已被涂黑(图中阴影部分),若在其余网格中再涂黑一个小正方形,使它与5个已被涂黑的小正方形组成的新图形是一个轴对称图形,则可涂黑的小正方形共有( )个.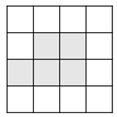 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
9. 把18个边长都为1的等边三角形如图拼接成平行四边形,且其中6个涂上了阴影,现在,可以旋转、翻折或平移某一个阴影等边三角形到某一个空白的等边三角形处,使新构成的阴影部分图案是轴对称图形,共可得种轴对称图形.
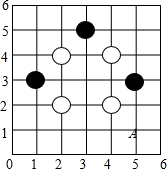
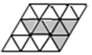 10. 如图是用围棋棋子在6×6的正方形网格中摆出的图案,棋子的位置用有序实数对表示,如A点为(5,1),若再摆一黑一白两枚棋子,使这9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是(请填写正确答案的序号)
10. 如图是用围棋棋子在6×6的正方形网格中摆出的图案,棋子的位置用有序实数对表示,如A点为(5,1),若再摆一黑一白两枚棋子,使这9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是(请填写正确答案的序号)①黑(1,5),白(5,5);②黑(3,2),白(3,3);③黑(3,3),白(3,1);④黑(3,1),白(3,3)
 11. 在下列图案中可以用旋转得到的是(填序号).
11. 在下列图案中可以用旋转得到的是(填序号).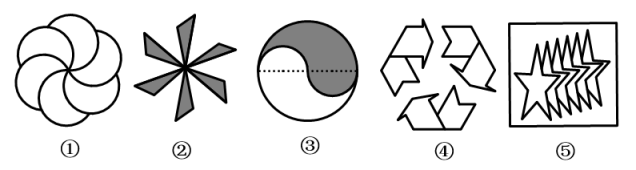 12. 如图,在平面直角坐标系xOy中,△OCD可以看作是△ABO经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△ABO得到△OCD的过程:.
12. 如图,在平面直角坐标系xOy中,△OCD可以看作是△ABO经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△ABO得到△OCD的过程:.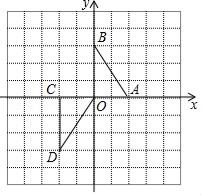 13. “皮克定理”是用来计算顶点在格点(即图中虚线的交点,如图中的小黑点)上的多边形的面积公式,公式为S = a + -1.小明只记得公式中的表示多边形的面积,a 和 b 中有一个表示多边形边上(含多边形顶点)的格点个数,另一个表示多边形内部的格点个数,但记不清楚究竟是哪一个表示多边形内部的格点个数,请你利用图 1 探究并运用探究的结果求图 2 中多边形的面积是.
13. “皮克定理”是用来计算顶点在格点(即图中虚线的交点,如图中的小黑点)上的多边形的面积公式,公式为S = a + -1.小明只记得公式中的表示多边形的面积,a 和 b 中有一个表示多边形边上(含多边形顶点)的格点个数,另一个表示多边形内部的格点个数,但记不清楚究竟是哪一个表示多边形内部的格点个数,请你利用图 1 探究并运用探究的结果求图 2 中多边形的面积是.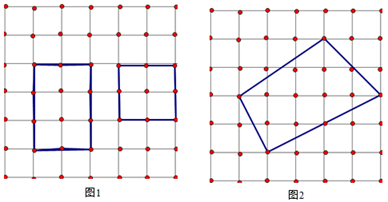
三、解答题
-
14. 如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有多少个?请分别在下图中涂出来,并画出这个轴对称图形的对称轴.

 15. 如图,是由4×4个大小完在一样的小正方形组成的方格纸,其中有两个小正方形是涂黑的,请再选择三个小正方形并涂黑,使图中涂黑的部分成为轴对称图形.并画出它的一条对称轴(如图例.画对一个得1分)
15. 如图,是由4×4个大小完在一样的小正方形组成的方格纸,其中有两个小正方形是涂黑的,请再选择三个小正方形并涂黑,使图中涂黑的部分成为轴对称图形.并画出它的一条对称轴(如图例.画对一个得1分)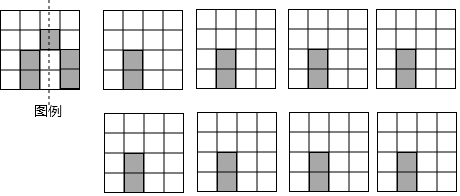
四、综合题
-
16. 如图都是由边长为1的小等边三角形构成的网格图,每个网格图中有3个小等边三角形已涂上阴影.
 (1)、请在下面①②③三个网格图中分别涂上一个三角形,使得4个阴影小等边三角形组成一个轴对称图形(3个图形中所涂三角形不同);(2)、在④⑤两个网格图中分别涂上一个三角形,使得4个阴影小等边三角形组成一个中心对称图形(2个图形中所涂三角形不同).17. 图1,图2都是由边长为1的小等边三角形构成的网格,每个网格图中有3个小等边三角形已涂上阴影.请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影:
(1)、请在下面①②③三个网格图中分别涂上一个三角形,使得4个阴影小等边三角形组成一个轴对称图形(3个图形中所涂三角形不同);(2)、在④⑤两个网格图中分别涂上一个三角形,使得4个阴影小等边三角形组成一个中心对称图形(2个图形中所涂三角形不同).17. 图1,图2都是由边长为1的小等边三角形构成的网格,每个网格图中有3个小等边三角形已涂上阴影.请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影: (1)、使得4个阴影小等边三角形组成一个轴对称图形.(2)、使得4个阴影小等边三角形组成一个中心对称图形.(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
(1)、使得4个阴影小等边三角形组成一个轴对称图形.(2)、使得4个阴影小等边三角形组成一个中心对称图形.(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)