2023-2024学年湘教版初中数学七年级下学期 5.2 旋转同步分层训练培优题
试卷更新日期:2024-03-26 类型:同步测试
一、选择题
-
1. 在平面直角坐标系中,把点P(2,3)绕原点旋转90°得到点P1 , 则点P1的坐标是( )A、(﹣3,2) B、(﹣2,3) C、(﹣2,3)或(2,﹣3) D、(﹣3,2)或(3,﹣2)2. 小明将图
 案绕某点连续旋转若干次,每次旋转相同角度 , 设计出一个外轮廓为正六边形的图案(如图),则可以为( )
案绕某点连续旋转若干次,每次旋转相同角度 , 设计出一个外轮廓为正六边形的图案(如图),则可以为( ) A、30° B、60° C、90° D、120°3. 如图,将三角形AOB绕点O按逆时针方向旋转后得到三角形COD , 若 , 则的度数是( )
A、30° B、60° C、90° D、120°3. 如图,将三角形AOB绕点O按逆时针方向旋转后得到三角形COD , 若 , 则的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、 4. 如图,在的方格纸中,格点(三个顶点都是格点的三角形)经过旋转后得到格点 , 则其旋转中心是( )
4. 如图,在的方格纸中,格点(三个顶点都是格点的三角形)经过旋转后得到格点 , 则其旋转中心是( )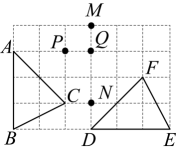 A、格点M B、格点N C、格点P D、格点Q5. 如图,把三角形绕点C顺时针旋转 , 得到三角形 . 若 , 则的度数为( )
A、格点M B、格点N C、格点P D、格点Q5. 如图,把三角形绕点C顺时针旋转 , 得到三角形 . 若 , 则的度数为( ) A、 B、 C、 D、6. 在新型俄罗斯方块游戏中(出现的图案可进行顺时针、逆时针旋转.向左、向右平移)。已拼好的图形如图所示.现又出现一个图案正向下运动,若要使该图案与下面的图形拼成一个完整的矩形。则该图案需进行的操作是( )
A、 B、 C、 D、6. 在新型俄罗斯方块游戏中(出现的图案可进行顺时针、逆时针旋转.向左、向右平移)。已拼好的图形如图所示.现又出现一个图案正向下运动,若要使该图案与下面的图形拼成一个完整的矩形。则该图案需进行的操作是( ) A、顺时针旋转90°,向右平移至最右侧 B、逆时针旋转90°,向右平移至最右侧 C、顺时针旋转90°,向左平移至最左侧 D、逆时针旋转90°,向左平移至最左侧7. 如图,在△OAB中,顶点O(0,0),A(﹣2,3),B(2,3),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第2023次旋转结束时,点D的坐标为( )
A、顺时针旋转90°,向右平移至最右侧 B、逆时针旋转90°,向右平移至最右侧 C、顺时针旋转90°,向左平移至最左侧 D、逆时针旋转90°,向左平移至最左侧7. 如图,在△OAB中,顶点O(0,0),A(﹣2,3),B(2,3),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第2023次旋转结束时,点D的坐标为( ) A、(﹣2,7) B、(7,2) C、(2,﹣7) D、(﹣7,﹣2)8. 如图,在平面直角坐标系中,四边形是矩形,点 , , 将矩形绕点逆时针旋转 , 则旋转后点的对应点坐标为( )
A、(﹣2,7) B、(7,2) C、(2,﹣7) D、(﹣7,﹣2)8. 如图,在平面直角坐标系中,四边形是矩形,点 , , 将矩形绕点逆时针旋转 , 则旋转后点的对应点坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 在直角坐标系中,点(4,5)绕原点O逆时针方向旋转90°,得到的点的坐标是.10. 如图,将含60°角的直角三角形ABC绕顶点A顺时针旋转45°度后得到△AB′C′,点B经过的路径为弧BB′.若∠BAC=60°,AC=1,则图中阴影部分的面积是
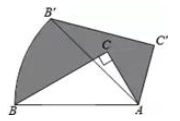 11. 如图所示,将一个顶角∠B=30°的等腰三角形ABC绕点A顺时针旋转α(0°<α<180°),得到等腰三角形AB'C',使得点B',A , C在同一条直线上,则旋转角α=度.
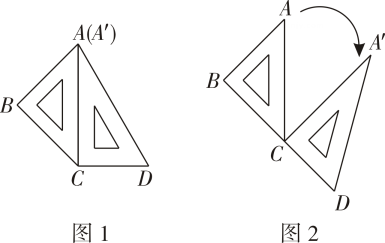
11. 如图所示,将一个顶角∠B=30°的等腰三角形ABC绕点A顺时针旋转α(0°<α<180°),得到等腰三角形AB'C',使得点B',A , C在同一条直线上,则旋转角α=度. 12. 两块不同的三角板按如图1所示摆放,边与边重合, , 接着如图2保持三角板不动,将三角板绕着点(点不动)按顺时针(如图标示方向)旋转,在旋转的过程中,逐渐增大,当第一次等于时,停止旋转,在此旋转过程中,时,三角板有一条边与三角板的一条边恰好平行.
12. 两块不同的三角板按如图1所示摆放,边与边重合, , 接着如图2保持三角板不动,将三角板绕着点(点不动)按顺时针(如图标示方向)旋转,在旋转的过程中,逐渐增大,当第一次等于时,停止旋转,在此旋转过程中,时,三角板有一条边与三角板的一条边恰好平行.
 13. 如图1,O为直线上一点,作射线 , 使 , 将一个直角三角尺如图摆放,直角顶点在点O处,一条直角边在射线上.将图1中的三角尺绕点O以每秒的速度按逆时针方向旋转(如图2所示),在旋转一周的过程中:
13. 如图1,O为直线上一点,作射线 , 使 , 将一个直角三角尺如图摆放,直角顶点在点O处,一条直角边在射线上.将图1中的三角尺绕点O以每秒的速度按逆时针方向旋转(如图2所示),在旋转一周的过程中: (1)、当旋转10秒时,则的度数;(2)、第t秒时,所在直线恰好平分 , 则t的值为 .
(1)、当旋转10秒时,则的度数;(2)、第t秒时,所在直线恰好平分 , 则t的值为 .三、解答题
-
14. 以直线上一点O为端点,在直线的上方作射线 , 使 , 将一个直角三角板的直角顶点放在O处,即 , 直角三角板可绕顶点O转动,在转动的过程中,直角三角板所有部分始终保持在直线上或上方.
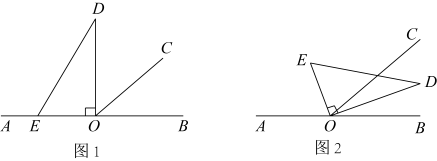 (1)、如图1,若直角三角板的一边在射线上,则;(2)、将直角三角板绕点O转动后,使其一边在的内部,如图2所示,
(1)、如图1,若直角三角板的一边在射线上,则;(2)、将直角三角板绕点O转动后,使其一边在的内部,如图2所示,①若恰好平分 , 求此时的度数;
②若 , 求此时的度数;
(3)、直角三角板在绕点O转动的过程中,与之间存在一定的数量关系,请直接写出来,不必说明理由.15. 如图1,将两块直角三角板(一块含有、角,另一块含角)摆放在直线上,三角板绕点以每秒的速度逆时针旋转.当第一次与射线重合时三角板停止转动,设旋转时间为秒.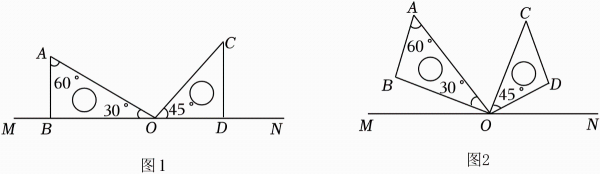 (1)、当时,求和的度数;(2)、如图2,若两块三角板同时旋转,三角板以每秒的速度绕点顺时针旋转,当第一次与射线重合时三角板立即停止转动.
(1)、当时,求和的度数;(2)、如图2,若两块三角板同时旋转,三角板以每秒的速度绕点顺时针旋转,当第一次与射线重合时三角板立即停止转动.①用含的代数式表示射线和射线重合前和的度数;
②整个旋转过程中,当满足时,求出相应的的值.
四、综合题
-
16. 如图1, 已知 ,射线 从 位置出发,以每秒 的速度按顺时针方向向射线 旋转;与此同时, 射线 以每秒 的速度,从 位置出发按逆时针方向向射线 旋转,到达射线 后又以同样的速度按顺时针方向返回,当射线 与射线 重合时,两条射线同时停止运动,设旋转时间为t(s).
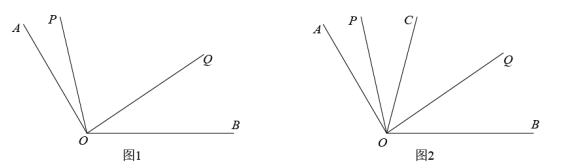 (1)、当 时, 求 的度数;(2)、当 与 重合时,求 的值;(3)、如图2,在旋转过程中, 若射线 始终平分 ,问:是否存在 的值, 使得 若存在,请直接写出 的值;若不存在,请说明理由.17. 如图,有一副直角三角板如图放置(其中 , ), , 与直线重合,且三角板 , 三角板均可以绕点逆时针旋转.
(1)、当 时, 求 的度数;(2)、当 与 重合时,求 的值;(3)、如图2,在旋转过程中, 若射线 始终平分 ,问:是否存在 的值, 使得 若存在,请直接写出 的值;若不存在,请说明理由.17. 如图,有一副直角三角板如图放置(其中 , ), , 与直线重合,且三角板 , 三角板均可以绕点逆时针旋转. (1)、在图1中,;(2)、①如图2,若三角板保持不动,三角板绕点逆时针旋转,转速为秒,转动一周三角板就停止转动,在旋转的过程中,当旋转时间为多少时,有成立;
(1)、在图1中,;(2)、①如图2,若三角板保持不动,三角板绕点逆时针旋转,转速为秒,转动一周三角板就停止转动,在旋转的过程中,当旋转时间为多少时,有成立;②如图 , 在图基础上,若三角板的边从处开始绕点逆时针旋转,转速为秒,同时三角板的边从处开始绕点逆时针旋转,转速为秒,当转到与位置重合时,两三角板都停止转动,在旋转过程中,当时,求旋转的时间是多少?