2023-2024学年湘教版初中数学七年级下学期 5.1.2 轴对称变换同步分层训练培优题

试卷更新日期：2024-03-26 类型：同步测试

进入出卷网下载

一、选择题

1. 小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形，她对折了（　　）

A、1次 B、2次 C、3次 D、4次

查看试题解析
2. 如图，将长方形纸片ABCD折叠，使点D与点B重合，点C落在点 $C^{'}$ 处，折痕为EF，若∠ABE＝30°，则 $∠ E F C^{'}$ 的度数为（）

A、120° B、100° C、150° D、90°

查看试题解析
3. 如图，把矩形ABCD沿EF对折后使两部分重合，若∠1＝50°，则∠BFE＝（　　）

A、70° B、65° C、60° D、50°

查看试题解析
4. 已知点P（m﹣1，4）与点Q（2，n﹣2）关于x轴对称，则mⁿ的值为（　　）

A、9 B、﹣9 C、 $- \frac{1}{9}$ D、 $\frac{1}{9}$

查看试题解析
5. 折纸是我国的传统文化，折纸不仅和自然科学结合在一起，还发展出了折纸几何学，成为现代几何学的一个分支，折纸过程中既要动脑又要动手．如图，将一长方形纸条首先沿着 $E F$ 进行第一次折叠，使得 $C$ ， $D$ 两点落在 $C_{1}$ 、 $D_{1}$ 的位置，再将纸条沿着 $G F$ 折叠（ $G F$ 与 $B C$ 在同一直线上），使得 $C_{1}$ 、 $D_{1}$ 分别落在 $C_{2}$ 、 $D_{2}$ 的位置．若 $3 ∠ E F B = ∠ E F C_{2}$ ，则 $∠ G E F$ 的度数为（）

A、 $30 °$ B、 $36 °$ C、 $45 °$ D、 $60 °$

查看试题解析
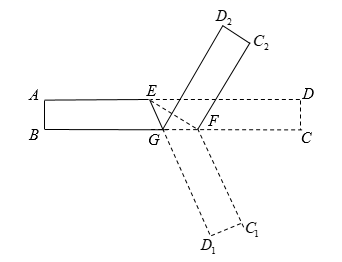6. 如图，在平面直角坐标系中，长为2的线段AB（点B在点A上面）在y轴上移动，C（1，0），D（4，0），连接AC ， BD ，则AC+BD的最小值为（　　）

A、5 B、 $3 \sqrt{3}$ C、2 $\sqrt{7}$ D、 $\sqrt{29}$

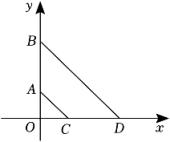查看试题解析
7. 如图，方格纸中每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，线段AB的顶点均在格点上．在图中画一条不与AB重合的线段MN ，使MN与AB关于某条直线对称，且M ， N均为格点，这样的线段能画（　　）条．

A、2 B、3 C、5 D、6

查看试题解析
8. 如图，在菱形ABCD中，AC与BD相交于点O，AB＝4，BD＝ $4 \sqrt{3}$ ， E为AB的中点，点P为线段AC上的动点，则EP＋BP的最小值为（）

A、4 B、 $2 \sqrt{5}$ C、 $2 \sqrt{7}$ D、8

查看试题解析

二、填空题

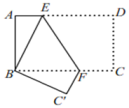
9. 点E(a，－5)与点F(－2，b)关于y轴对称，则a＝， b＝.

查看试题解析
10. 将五边形ABCDE按如图方式折叠，折痕为AF．点E、D分别落在E′，D′．已知∠AFC＝76°，则∠CFD′＝．

查看试题解析
11. 如图，已知长方形纸片ABCD ，点E在AB上，将三角形ADE沿DE折叠，点A落在点A'处，连接EA'并延长交CD于点F ，将∠BEF对折，点B落在直线EF上的点B'处，折痕为EM ，则∠DEM的度数是．

查看试题解析
12. 如图1是一张长方形纸带，∠DEF=20°，若将纸带沿EF折叠成图2，再沿BF折叠成图3，则图3中的∠CFE的度数为°.

查看试题解析
13. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ， $∠ A = 30 °$ ， $A B = 3$ ， $B C = \sqrt{3}$ ，点 $D$ 是边 $A C$ 上一动点．连接 $B D$ ，将 $△ A B D$ 沿 $B D$ 折叠，得到 $△ E B D$ ，其中点 $A$ 落在 $E$ 处， $B E$ 交 $A C$ 于点 $F$ ，当 $△ E D F$ 为直角三角形时， $E F$ 长度是．

查看试题解析

三、解答题

14. 利用折纸可以作出角平分线．

(1)、如图1，若 $∠ A O B = 58 °$ ，则 $∠ B O C =$ ；

(2)、折叠长方形纸片， $O C$ ， $O D$ 均是折痕，折叠后，点A落在点 $A^{'}$ ，点 $B$ 落在点 $B^{'}$ ，连接 $O A^{^{'}}$ ．
①如图2，当点 $B^{'}$ 在 $O A^{^{'}}$ 上时，判断 $∠ A O C$ 与 $∠ B O D$ 的关系，并说明理由；
②如图3，当点 $B^{'}$ 在 $∠ C O A^{'}$ 的内部时，连接 $O B^{^{'}}$ ，若 $∠ A O C = 44 °$ ， $∠ B O D = 61 °$ ，求 $∠ A^{'} O B^{'}$ 的度数．

查看试题解析
15. 如图，在一个长方形纸条上画一个数轴，解答下面的问题：

(1)、如图，将纸条折叠，使数轴上的点A与表示一5的点重合，易知折痕与数轴的交点表示的有理数为-2；若将纸条折叠，数轴上的点A与表示-6的点重合，则折痕与数轴的交点表示的有理数为；

(2)、若数轴上M、N两点之间的距离为2020 (M在N的左侧)，将数轴折叠，使折痕与数轴交点表示的有理数为100，此时数轴上M、N两点恰好重合，求点M和点N表示的有理数。

查看试题解析

四、综合题

16. 问题解决：

(1)、问题情境：如图1所示，要在街道旁修建一个奶站，向居民区A、B提供牛奶，奶站应建在什么地方，才能使从A、B到P的距离之和最短？请画出点P的位置；

(2)、问题理解：如图2，在△ABC中，AB＝AC，AD平分∠BAC，点E是AC边的中点，点P是线段AD上的动点，画出PC＋PE取得最小值时点P的位置；

(3)、问题运用：如图3，在△ABC中，AB＝AC＝13，BC＝10，AD＝12，AD是∠BAC的平分线，当点E、P分别是AC和AD上的动点时，求PC＋PE的最小值．

查看试题解析
17. 综合与实践课上，同学们动手折叠一张正方形纸片ABCD ，如图1，其中E点在边AD上，F、G分别在边AB、CD上，分别以EF、EG为折痕进行折叠并压平，点A、D的对应点分别是点 $A^{'}$ 和点 $D^{'}$ .
甲同学的操作如图2；其中 $∠ F E G = 120 °$ ；
乙同学的操作如图3， $A^{'}$ 落在 $E D^{'}$ 所在直线上；
丙同学的操作如图4， $A^{'}$ 落在EG上， $D^{'}$ 落在EF上.

(1)、求出图2中 $∠ A^{'} E D^{'}$ 的度数；

(2)、直接写出图3中 $∠ F E G$ 的度数；

(3)、直接写出图4中 $∠ F E G$ 的度数；

(4)、若折叠后 $∠ A^{'} E D^{'} = n °$ ，直接写出 $∠ F E G$ 的度数（用含n的代数式表示）.

查看试题解析