2023-2024学年湘教版初中数学七年级下学期 5.1.2 轴对称变换同步分层训练基础题
试卷更新日期:2024-03-26 类型:同步测试
一、选择题
-
1. 已知点的坐标为则点关于x轴对称的点的坐标为( )A、 B、 C、 D、2. 已知点A(m,2022)与点B(2023,n)关于y轴对称,则m+n的值为( )A、﹣1 B、1 C、4043 D、﹣20223. 如图是战机在空中展示的轴对称队形.以飞机B , C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机E的坐标为(40,a),则飞机D的坐标为( )
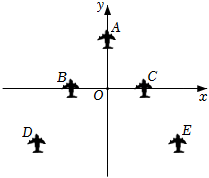 A、(40,-a) B、(-40,a) C、(-40,-a) D、(a , -40)4. 已知点P(1,﹣2)与点Q关于x轴对称,则点Q的坐标为( )A、(1,2) B、(﹣1,﹣2) C、(﹣2,1) D、(﹣1,2)5. 在平面直角坐标系中,点 关于 轴对称的点的坐标为( )A、 B、 C、 D、6. 如图,这是平面镜成像的示意图,若以蜡烛的底部和平面镜中像的底部连线为轴,平面镜所在点的竖线为轴(镜面厚度忽略不计)建立平面直角坐标系,某时刻火焰顶部的坐标是 , 则此时对应的虚像的坐标是( )
A、(40,-a) B、(-40,a) C、(-40,-a) D、(a , -40)4. 已知点P(1,﹣2)与点Q关于x轴对称,则点Q的坐标为( )A、(1,2) B、(﹣1,﹣2) C、(﹣2,1) D、(﹣1,2)5. 在平面直角坐标系中,点 关于 轴对称的点的坐标为( )A、 B、 C、 D、6. 如图,这是平面镜成像的示意图,若以蜡烛的底部和平面镜中像的底部连线为轴,平面镜所在点的竖线为轴(镜面厚度忽略不计)建立平面直角坐标系,某时刻火焰顶部的坐标是 , 则此时对应的虚像的坐标是( ) A、 B、 C、 D、7. 如图,在4×4的正方形网格中,已有四个小正方形被涂黑.若将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形,则该小正方形的位置可以是( )
A、 B、 C、 D、7. 如图,在4×4的正方形网格中,已有四个小正方形被涂黑.若将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形,则该小正方形的位置可以是( ) A、(一,2) B、(二,4) C、(三,2) D、(四,4)8. 在平面直角坐标系中,若干个边长为个单位长度的等边三角形,按如图中的规律摆放点从原点出发,以每秒个单位长度的速度沿着等边三角形的边“”的路线运动,设第秒点运动到点为正整数 , 则点的坐标是( )
A、(一,2) B、(二,4) C、(三,2) D、(四,4)8. 在平面直角坐标系中,若干个边长为个单位长度的等边三角形,按如图中的规律摆放点从原点出发,以每秒个单位长度的速度沿着等边三角形的边“”的路线运动,设第秒点运动到点为正整数 , 则点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 若点P(4,3)关于y轴的对称点是点P'(a+1,b-2),则a= , b= .10. 在平面直角坐标系中,点与点关于x轴对称,则 .11. 如图,把一张长方形纸条ABCD沿EF折叠,若 , 则°
 12. 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿着直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为 cm.
12. 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿着直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为 cm.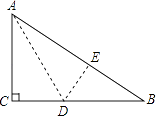 13. 已知和关于x轴对称,则的值为.
13. 已知和关于x轴对称,则的值为.三、解答题
-
14. 如图1,将长方形纸片ABCD沿MN折叠得到图2,点A,B的对应点分别为A',B',折叠后A'M与CN相交于点E.
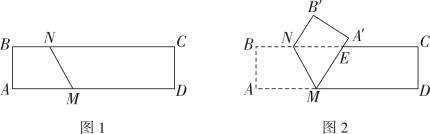 (1)、若 , 求∠A'MD的度数.(2)、设∠B'NC=α,∠A'MN=β.
(1)、若 , 求∠A'MD的度数.(2)、设∠B'NC=α,∠A'MN=β.①请用含α的代数式表示β.
②当MA'恰好平分∠DMN时,求∠A'MD的度数.
15. 请仔细观察如图所示的折纸过程,然后回答下列问题: (1)、的度数为;(2)、与的数量关系为;(3)、若 , 直接写出和的度数。
(1)、的度数为;(2)、与的数量关系为;(3)、若 , 直接写出和的度数。四、综合题
-
16. 阅读下列一段文字:已知在平面内两点P1(x1 , y1),P2(x2 , y2),其两点间的距离P1P2=
问题解决:已知A(1,4),B(7,2)
(1)、试求A , B两点的距离;(2)、在x轴上找一点P(不求坐标,画出图形即可),使PA+PB的长度最短,求PA+PB的最短长度.17. 如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴. (1)、如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1 , △A1B1C1关于直线l的对称图形是△A2B2C2 , 写出△A2B2C2的三个顶点的坐标;(2)、如果点P的坐标是(﹣a,0),其中0<a<3,点P关于y轴的对称点是P1 , 点P1关于直线l的对称点是P2 , 求PP2的长.
(1)、如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1 , △A1B1C1关于直线l的对称图形是△A2B2C2 , 写出△A2B2C2的三个顶点的坐标;(2)、如果点P的坐标是(﹣a,0),其中0<a<3,点P关于y轴的对称点是P1 , 点P1关于直线l的对称点是P2 , 求PP2的长.