2023-2024学年湘教版初中数学七年级下学期 4.5 垂线同步分层训练培优题
试卷更新日期:2024-03-26 类型:同步测试
一、选择题
-
1. 在同一平面内,过直线l外一点P作l的垂线m,再过点P作m的垂线n ,则直线l与n的位置关系是( )A、相交 B、相交且垂直 C、平行 D、不能确定2. 若P,Q是直线AB 外不重合的两点,则下列说法中,错误的是 ( )A、直线 PQ可能与直线 AB 垂直 B、直线 PQ可能与直线 AB 平行 C、过点 P 的直线一定能与直线AB 相交 D、过点Q只能画出一条直线与直线AB 平行3. 如图, , 平分 , 平分 , , , 则下列结论:

;
;
;
.
其中正确结论有个.( )
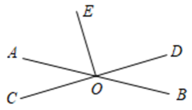
A、 B、 C、 D、4. 如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:①OG⊥AB;②OF平分∠BOD;③∠AOE=65°;④∠GOE=∠DOF,其中正确的有 ( ) A、1个 B、2个 C、3个 D、4个5. 如图,AB∥CD,∠C=70°,BE⊥BC,则∠ABE等于( )
A、1个 B、2个 C、3个 D、4个5. 如图,AB∥CD,∠C=70°,BE⊥BC,则∠ABE等于( ) A、20° B、30° C、35° D、60°6. 如图, , 直线交于点E , 过点E作;交于点F , 若 . 则的度数为( )
A、20° B、30° C、35° D、60°6. 如图, , 直线交于点E , 过点E作;交于点F , 若 . 则的度数为( ) A、 B、 C、 D、7. 小强在科学课上学过平面镜成像知识后,在老师的带领下到某厂房做验证实验,如图,老师在该厂房房檐处安装一平面镜 , 与墙面所成的角为 , 房顶与水平地面平行,小强在点M的正下方C处观察平面镜,恰能在M点看到水平地面上的点D.则的度数为( )
A、 B、 C、 D、7. 小强在科学课上学过平面镜成像知识后,在老师的带领下到某厂房做验证实验,如图,老师在该厂房房檐处安装一平面镜 , 与墙面所成的角为 , 房顶与水平地面平行,小强在点M的正下方C处观察平面镜,恰能在M点看到水平地面上的点D.则的度数为( ) A、 B、 C、 D、8. 下列说法中正确的个数为( )
A、 B、 C、 D、8. 下列说法中正确的个数为( )①过一点有且只有一条直线与已知直线垂直;
②两条直线被第三条直线所截,同位角相等;
③经过两点有一条直线,并且只有一条直线;
④在同一平面内,不重合的两条直线不是平行就是相交.
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 如图,直线AB,CD相交于点O,若∠BOD=30°,OE⊥CD,则∠AOE的度数为 .
 10. 如图,已知直线 , 点B在直线a上,点A、C在直线b上,且 . 若 , 则的度数为 .
10. 如图,已知直线 , 点B在直线a上,点A、C在直线b上,且 . 若 , 则的度数为 . 11. 如图,直线 , 相交于点 , 射线垂直于且平分 , 若 , 则的度数是 .
11. 如图,直线 , 相交于点 , 射线垂直于且平分 , 若 , 则的度数是 . 12. 如图,平面中两条直线和相交于点 , 对于平面上任意一点 , 若点到直线、的距离分别是、 , 则称有序实数对是点的“距离坐标”特别地,当点在直线上时,定义点到直线的距离为下列说法:
12. 如图,平面中两条直线和相交于点 , 对于平面上任意一点 , 若点到直线、的距离分别是、 , 则称有序实数对是点的“距离坐标”特别地,当点在直线上时,定义点到直线的距离为下列说法:
“距离坐标”是的点只有点;
“距离坐标”是的点只有个;
“距离坐标”是的点共有个;
正确的有 填序号 . 13. 如图, , , 平分 , , 有下列结论:①;②;③;④.其中正确的结论.(填写序号)
13. 如图, , , 平分 , , 有下列结论:①;②;③;④.其中正确的结论.(填写序号)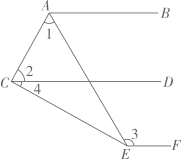 14. 如图,直线MN分别与直线AB,CD相交于点E,F,EG平分 , 交直线CD于点G,若 , 射线于点G,则.
14. 如图,直线MN分别与直线AB,CD相交于点E,F,EG平分 , 交直线CD于点G,若 , 射线于点G,则.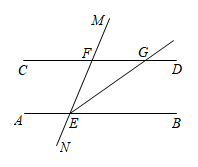
三、解答题
-
15. 已知, , 直线交于点 , 交于点 , 点在线段上,过作射线、分别交直线、于点、 .
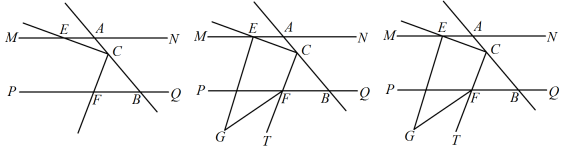 (1)、如图1,当时,求的度数;(2)、如图2,若和的角平分线交于点 , 求和的数量关系;(3)、如图3,在(2)的基础上,当 , 且 , 时,射线绕点以每秒的速度顺时针旋转,设运动时间为秒,当射线与的一边互相平行时,请直接写出的值.16. 如图,已知:于D , 过点D作交BC于E , 过点E作于F.
(1)、如图1,当时,求的度数;(2)、如图2,若和的角平分线交于点 , 求和的数量关系;(3)、如图3,在(2)的基础上,当 , 且 , 时,射线绕点以每秒的速度顺时针旋转,设运动时间为秒,当射线与的一边互相平行时,请直接写出的值.16. 如图,已知:于D , 过点D作交BC于E , 过点E作于F. (1)、补全图形;(2)、比较大小:EFEB , 其中的数学依据是:;(3)、请你猜想与的数量关系,并证明你的结论;(4)、若 , , 求的度数.
(1)、补全图形;(2)、比较大小:EFEB , 其中的数学依据是:;(3)、请你猜想与的数量关系,并证明你的结论;(4)、若 , , 求的度数.四、综合题
-
17. 如图,点C在射线BE上,点F在线段AD上,CD平分∠FCE,.

 (1)、当时,求∠DCE:(2)、点N是线段FD上一点,点P是线段CD上一点,连接AC,FP.若CA为∠BCF的角平分线, , , 探究直线CD上是否存在一点Q,使得.18. 如图,直线与的两边交于 , 两点, , 点是边上一个动点,连接 .
(1)、当时,求∠DCE:(2)、点N是线段FD上一点,点P是线段CD上一点,连接AC,FP.若CA为∠BCF的角平分线, , , 探究直线CD上是否存在一点Q,使得.18. 如图,直线与的两边交于 , 两点, , 点是边上一个动点,连接 .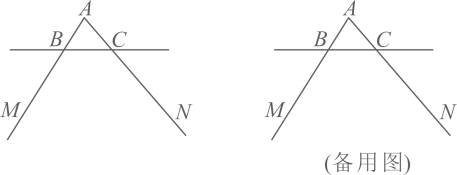 (1)、过点作 , 交射线于点 , 依题意补全图形,
(1)、过点作 , 交射线于点 , 依题意补全图形,①直接写出的度数(用含α的式子表示);
②若点 , 在 , 的延长线上,并且直线 , 当平分时,求的度数(用含的式子表示);小林在思考这道题时,想到过点作交射线于点 , 通过转化角可以求出的度数.你可以利用小林的思路解答此题也可以独立思考求出的度数.
(2)、参考小林思考问题的方法,解决问题:若点 , 在 , 的延长线上,并且直线 , 当点在上运动时,直接用含的等式表示 , , 的数量关系.