2023-2024学年湘教版初中数学七年级下学期 4.5 垂线同步分层训练提升题
试卷更新日期：2024-03-26 类型：同步测试
一、选择题
-
1. 下列结论中，错误的是（ ）A、同位角相等，两直线平行 B、同一平面内过一点有且只有一条直线与已知直线垂直 C、同一平面内的两条直线不平行就相交 D、过一点有且只有一条直线与已知直线平行2. 下列生活中的实例，数学原理解释错误的一项是（ ）A、从一条河向一个村庄引一条最短的水渠．可用的数学原理是：在同一平面内，过一点有且只有一条直线垂直于已知直线 B、两个村庄之间修一条最短的公路．可用的数学原理是：两点之间线段最短 C、把一根木条固定到墙上需要两颗钉子．可用的数学原理是：两点确定一条直线 D、从一个物流仓库向高速公路修一条最短的马路．可用的数学原理是：连结直线外一点与直线上各点的所有线段中，垂线段最短3. 如图，点 ， 在直线上，点 ， 在直线上， ， ， ， 点到直线的距离是（ ）
A、线段的长度 B、线段的长度 C、线段的长度 D、线段的长度4. 如图， ， 若 ， 则的度数为（ ）
A、35° B、45° C、50° D、55°5. 如图1，汉代初期的《淮南万毕术》是中国古代有关物理、化学的重要文献，书中记载了我国古代学者在科学领域做过的一些探索及成就．其中所记载的“取大镜高悬，置水盆于其下，则见四邻矣”，是古人利用光的反射定律改变光路的方法，即“反射光线与入射光线、法线在同一平面上；反射光线和入射光线位于法线的两侧；反射角等于入射角”．为了探清一口深井的底部情况，运用此原理，如图在井口放置一面平面镜可改变光路，当太阳光线与地面所成夹角时，要使太阳光线经反射后刚好垂直于地面射入深井底部，则需要调整平面镜与地面的夹角（ ）
A、 B、 C、 D、6. 如图，把小河里的水引到田地A处，若使水沟最短，则过点A向河岸l作垂线，垂足为点B，沿AB挖水沟即可，理由是（ ）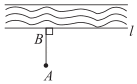
A、两点之间，线段最短 B、垂线段最短 C、两点确定一条直线 D、过一点可以作无数条直线7. 小明制作简易工具来测量物体表面的倾斜程度，方法如下：将刻度重新设计的量角器固定在等腰直角三角板上，使量角器的刻度线与三角板的底边平行将用细线和铅锤做成的重锤线顶端固定在量角器中心点处，现将三角板底边紧贴被测物体表面，如图所示，此时重锤线在量角器上对应的刻度为 ， 那么被测物体表面的倾斜角为（ ）
A、 B、 C、 D、8. 如图， ， 平分 ， ， ， ， 则下列结论：
；平分；； ．
其中正确结论的个数是（ ）
A、个 B、个 C、个 D、个二、填空题
-
9. 如图，直线AB，CD相交于点O，OE⊥CD，垂足为点O．若∠BOE=40°6'，则∠AOC的度数为
10. 下列三个日常现象：
其中，可以用“垂线段最短”来解释的是 （填序号）．
11. 如图，为的边上一点，过点作 ， 交的平分线于点 ． 过点作 ， 交的延长线于点 ， 若 ． 现有以下结论：①；②；③；④ ． 其中正确的是 ． （填序号）
12. 如图，已知 ， 直线分别与直线、交于点、 ， 平分 ， 交于点 ， 交于点 ， 若 ， 则 ．
13. 如图，直线 ， 直线c与直线a，b分别交于点E、F，射线直线c，若 ， 则的度数是 ．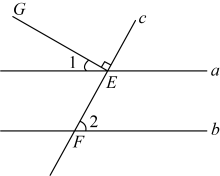
三、解答题
-
14. 如图①．在四边形ABCD中．∠ABC+∠ADC=180°，BE、DF分别是∠ABC与∠ADC的平分线，∠ADF与∠AFD互余．
(1)、试判断直线BE与DF的位置关系．并说明理由．(2)、如图②，延长CB、DF相交于点G，过点B作BH⊥FG，垂足为H．试判断∠FBH与∠GBH的大小关系，并说明理由．15. 填空：如图，AB⊥BC，BC⊥CD，且∠1=∠2，试说明：BE∥CF.
解：∵AB⊥BC，BC⊥CD（已知），
∴ ▲ = ▲ =90°（ ）.
又∵∠1=∠2（已知），
∴ ▲ = ▲ （等式的性质），
∴BE∥CF（ ）.
四、综合题
