2023-2024学年湘教版初中数学七年级下学期 4.4 平行线的判定同步分层训练培优题
试卷更新日期：2024-03-26 类型：同步测试
一、选择题
-
1. 如图，点E在AC 的延长线上，下列条件中，不能判定 BD∥AC的是（ ）
A、∠3=∠4 B、∠1=∠2 C、∠D=∠DCE D、∠D+∠ACD=180°2. 如图，直线 ， ∠1、∠2和∠3的数量关系是（ ）
A、 B、 C、 D、3. 如图能判断的是（ ）
A、 B、 C、 D、4. 木条a、b、c如图用螺丝固定在木板上，且∠ABM=50°，∠DEM=70°，将木条a、b、c看作是在同一平面内的三条直线AC、DF、MN若使直线AC、DF达到平行的位置关系，则下列描述错误的是（ ）
A、木条b、c固定不动，木条a绕点B顺时针旋转20° B、木条b、c固定不动，木条a绕点B逆时针旋转160° C、木条a、c固定不动，木条b绕点E逆时针旋转20° D、木条a、c固定不动，木条b绕点E顺时针旋转110°5. 如图，给出下列条件：①∠1=∠3；②∠2=∠3；③∠4=∠5；④∠2+∠4=180°．其中能判定直线l1∥l2的有（ ）
A、1个 B、2个 C、3个 D、4个6.如图，不能判定AB∥DF的是（ ）
A、∠1=∠2 B、∠A=∠4 C、∠1=∠A D、∠A+∠3=180°7. 如图： ， 平分 ， 平分 ， ， 则下列结论：①；②；③；④ ， 其中正确的是（ ）
A、①②③ B、①②④ C、②③④ D、①②③④8. 如图， ， 将一副直角三角板作如下摆放， ， ． 下列结论：①；②；③；④ ． 其中正确的个数是（ ）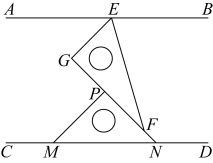
A、1 B、2 C、3 D、4二、填空题
-
9. 一节数学实践课上，老师让同学们用两个大小、形状都相同的三角板画平行线AB、CD ， 并要说出自己做法的依据.小奇、小妙两位同学的做法如图：小奇说：“我做法的依据是：同位角相等，两直线平行.”则小妙做法的依据是.
10. 如图，点D，E，F分别是△ABC的边AB，AC，BC上的点．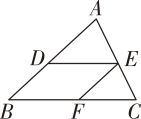
若∠B= ， 则EF∥AB；
若∠B= ， 则DE∥BC．
11. 一大门的栏杆如图，BA垂直地面AE于A，CD平行于地面AE，则∠ABC+∠BCD= ．
12. 如图， ， 在的两边上分别过点A和点C向同方向作射线和 ， 且 ， 若和的角平分线所在的直线交于点P（P与C不重合），则的大小为 ．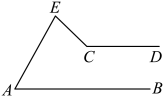
13. 如图，的角平分线、相交于F， ， ， 且于G．下列结论：①；②平分；③；④ ． 其中正确的结论是 ．
三、解答题
-
14. 如图，AB∥CD，直线EF与AB，CD分别相交于点G，H，∠EHD=α(0°<α<90°).小安将一个含30°角的直角三角尺PMN按如图1所示的方式放置，使点N，M分别在直线AB，CD上，且在点G，H的右侧，∠P=90°，∠PMN=60°.
(1)、∠PNB+∠PMD∠P(填“>”“<”或“=”).(2)、如图2，∠MNG的平分线NO交直线CD于点O.①当NO∥EF∥PM时，求α的度数.
②小安将三角尺PMN保持PM∥EF并向左平移，在平移的过程中求∠MON的度数(用含α的代数式表示).
15. 某地汛期来临，防汛指挥部在一危险地带两岸各安置了一探照灯，便于夜间查看江水及两岸河堤的情况.如图1，灯A射线自AM 顺时针旋转至AN 便立即回转，灯 B 射线自BP 顺时针旋转至BQ 便立即回转，两灯不停交叉照射巡视.若灯 A 转动的速度是a°/秒，灯 B转动的速度是b°/秒，且a，b满足|a-3b|+(a+b-4)²=0.假定这一带江堤是平行的，即PQ∥MN，且∠BAN=45°.
(1)、求a，b的值.(2)、若灯 B射线先转动30秒，灯A 射线才开始转动，在灯 B射线到达BQ 之前，灯 A 转动几秒，两灯的光束互相平行?(3)、如图2，两灯同时转动，在灯 A 射线到达AN 之前，若两灯射出的光束相交于点C，过点C作CD⊥AC，交 PQ 于点 D，则在转动过程中，∠BCD：∠BAC的值是否发生变化? 若不变，请求出该值；若改变，请求出其取值范围.四、综合题
