2023-2024学年湘教版初中数学七年级下学期 4.4 平行线的判定同步分层训练基础题
试卷更新日期：2024-03-26 类型：同步测试
一、选择题
-
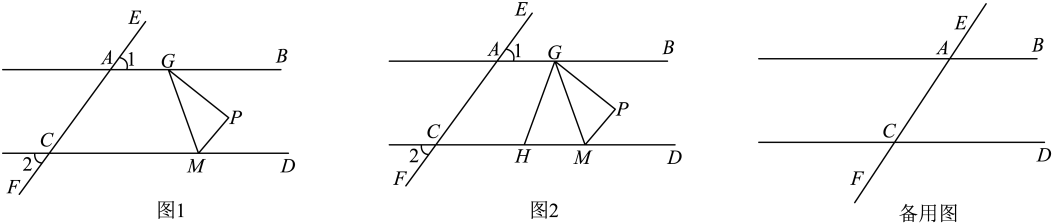
1. 如图，过直线外一点画已知直线的平行线的方法叫“推平行线”法(图中三角形是三角板)，其依据是（ ）
A、同旁内角互补，两直线平行 B、两直线平行，同旁内角互补 C、同位角相等，两直线平行 D、两直线平行，同位角相等2. 如图，下列条件中，能判定AB∥EF的是（ ）
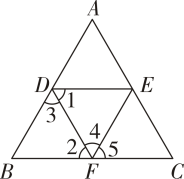
①∠B+∠BFE=180°；
②∠1=∠2；③∠3=∠4；
④∠B=∠5.A、② B、①③ C、①③④ D、②③④3. 下列图形中，根据∠1=∠2，能得到 AB∥CD 的是（ ）A、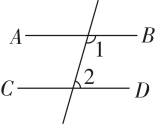
B、
C、
D、
4. 如图，直线a，b被直线c所截，当∠1=∠2=48°时，直线a，b的位置关系是（ ）
A、a∥b B、a∥b C、a⊥b D、无法确定5. 如图，下列条件中能判定是（ ）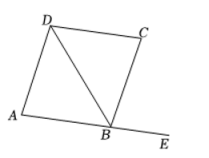
A、 B、 C、 D、6. 如图，点 E 在 BC 的延长线上，对于给出的四个条件：①∠1=∠3；②∠2+∠5=180°；③∠4=∠B；④∠D+∠BCD=180°.
其中能判定 AD∥BC的是（ ）
A、①② B、①④ C、①③ D、②④7. 如图，若∠3=∠4，则下列条件中，不能判定 AB∥CD的是（ ）
A、∠1=∠2 B、∠1=∠3 且∠2=∠4 C、∠1+∠3=90°且∠2+∠4=90° D、∠1+∠2=90°且∠3+∠4=90°8. 如图，直线a、b被直线c所截，下列条件中，不能判定的是（ ）
A、 B、 C、 D、二、填空题
-
9. 如图是小明学习三线八角时制作的模具，经测量，∠2=100°，要使木条a与b平行，则∠1的度数是°.
10. 如图，∠A=70°，O是AB上一点，直线OD与AB所夹角∠BOD=82°，要使OD∥AC，直线OD绕点O按逆时针方向至少旋转°
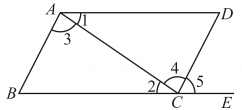
11. 如图，下列条件中，能判定AB∥CD的是(填序号).①∠B+∠BAD=180°；②∠1=∠2；③∠3=∠4；④∠BAD=∠2+∠4.
12. 如图，平面反光镜AC斜放在地面AB上，一束光线从地面上的P点射出，DE是反射光线.已知∠APD=120°，若要使反射光线DE∥AB，则∠CAB应调节为°(提示：∠ADP=∠CDE，三角形的内角和等于180°).
13. 填空：如图，用符号语言表达定理“同旁内角互补，两直线平行”.
∵ ， ∴a∥b.三、解答题
-
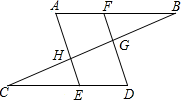
14. 如图，AB∥CD，点E在CD上，点G在DB的延长线上，连结EG，交AB于点F，连结AE.已知EA平分∠CEF，∠A=55°.
(1)、求∠BFG的度数.(2)、若∠A=∠D，试说明：∠AEF=∠G.15. 已知：如图，∠ABC=∠ADC，BF，DE分别平分∠ABC与∠ADC，且∠1=∠3.试说明：∠1+∠4=180°.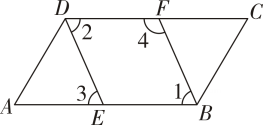
请将下列说理过程补充完整，并在括号内注明依据.
解：∵BF，DE分别平分∠ABC与∠ADC(已知)，
（ ） .
又∵∠ABC=∠ADC（ ），
∴∠1=∠2(等量代换).
又∵∠1=∠3(已知)，
∴∠2= ▲ （ ），
∴AB∥CD（ ），
∴∠1+∠4=180°（ ）
四、综合题
