2023-2024学年湘教版初中数学七年级下学期 4.3 平行线的性质同步分层训练培优题
试卷更新日期:2024-03-26 类型:同步测试
一、选择题
-
1. 如图,AB∥CD,∠B=60°,点C在BE上,下列结论中正确的是( )
 A、∠A=∠120° B、∠BCD=120° C、∠D=60° D、∠DCE=120°2. 如图,一块直角三角板的直角顶点放在直尺的一边上.若 , 则的大小是( )
A、∠A=∠120° B、∠BCD=120° C、∠D=60° D、∠DCE=120°2. 如图,一块直角三角板的直角顶点放在直尺的一边上.若 , 则的大小是( )
 A、 B、 C、 D、3. 如图,下列命题错误的是( )
A、 B、 C、 D、3. 如图,下列命题错误的是( ) A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么4. 光线在不同介质中的传播速度不同,因此当光线从空气射向水中时,会发生折射.如图,在空气中平行的两条入射光线,在水中的两条折射光线也是平行的.若水面和杯底互相平行,且 , 则( )
A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么4. 光线在不同介质中的传播速度不同,因此当光线从空气射向水中时,会发生折射.如图,在空气中平行的两条入射光线,在水中的两条折射光线也是平行的.若水面和杯底互相平行,且 , 则( ) A、 B、 C、 D、5. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心的光线相交于点 , 为焦点.若 , , 则的度数为( )
A、 B、 C、 D、5. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心的光线相交于点 , 为焦点.若 , , 则的度数为( ) A、 B、 C、 D、6. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺固定不动,将含角的三角尺绕顶点B顺时针转动(转动角度小于).当与三角尺的其中一条边所在的直线互相平行时,的度数是( )
A、 B、 C、 D、6. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺固定不动,将含角的三角尺绕顶点B顺时针转动(转动角度小于).当与三角尺的其中一条边所在的直线互相平行时,的度数是( )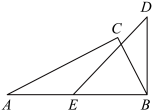 A、或或 B、或或 C、或或 D、或或7. 如图,已知 , , 点P是射线上一动点(与点A不重合),、分别平分和 , 分别交射线于点C、D,下列结论:①;②;③当时,;④当点P运动时,的数量关系不变.其中正确结论有( )个
A、或或 B、或或 C、或或 D、或或7. 如图,已知 , , 点P是射线上一动点(与点A不重合),、分别平分和 , 分别交射线于点C、D,下列结论:①;②;③当时,;④当点P运动时,的数量关系不变.其中正确结论有( )个 A、1 B、2 C、3 D、48. 如图, , , 平分 , 平分 , 则( )
A、1 B、2 C、3 D、48. 如图, , , 平分 , 平分 , 则( )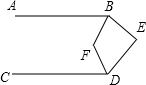 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,AB∥EG,CD∥EF,BC∥DE.若. =30°,则 z=°.
 10. 如图,AB∥CD,直线EF 分别交AB,CD于点E,F.∠BEF 的平分线交CD 于点G.若∠EFG=52°,则∠EGF 的度数为°.
10. 如图,AB∥CD,直线EF 分别交AB,CD于点E,F.∠BEF 的平分线交CD 于点G.若∠EFG=52°,则∠EGF 的度数为°. 11. 如图,含有角的直角三角板的两个顶点放在一个长方形的对边上,点为直角顶点, , 延长交于点 , 如果 , 那么的度数是 .
11. 如图,含有角的直角三角板的两个顶点放在一个长方形的对边上,点为直角顶点, , 延长交于点 , 如果 , 那么的度数是 . 12. 两块不同的三角板按如图所示摆放,边重合, , 接着如图保持三角板不动,将三角板绕着点按顺时针以每秒的速度旋转后停止在此旋转过程中,当旋转时间秒时,三角板有一条边与三角板的一条边恰好平行.
12. 两块不同的三角板按如图所示摆放,边重合, , 接着如图保持三角板不动,将三角板绕着点按顺时针以每秒的速度旋转后停止在此旋转过程中,当旋转时间秒时,三角板有一条边与三角板的一条边恰好平行. 13. 如图
13. 如图 (1)、如图一, , , , 则 .(2)、如图二, , , , , 分别平分和 , 则 , 满足的数量关系为 .
(1)、如图一, , , , 则 .(2)、如图二, , , , , 分别平分和 , 则 , 满足的数量关系为 .三、解答题
-
14. 将一副三角尺按如图1所示的方式摆放,直线GH∥MN,现将三角尺ABC绕点A 以每秒1°的速度顺时针旋转,同时三角尺 DEF 绕点D 以每秒2°的速度顺时针旋转,设旋转时间为 t秒,如图2,易知∠BAH=t°,∠FDM=2t°.若0≤t≤150,边 BC 与边 DE 平行,求满足条件的t的值.
 15. 将一副三角尺按如图所示的方式叠放在一起(其中∠A=60°,∠B=30°,∠ECD=∠EDC=45°,∠ACB=∠E=90°),将三角尺ABC绕点C按顺时针方向慢慢转动,转过180°后停止转动.
15. 将一副三角尺按如图所示的方式叠放在一起(其中∠A=60°,∠B=30°,∠ECD=∠EDC=45°,∠ACB=∠E=90°),将三角尺ABC绕点C按顺时针方向慢慢转动,转过180°后停止转动. (1)、当∠ACE=125°,∠BCD= .(2)、①当AB与CE平行时,求三角尺ABC转过的度数.
(1)、当∠ACE=125°,∠BCD= .(2)、①当AB与CE平行时,求三角尺ABC转过的度数.②在三角尺ABC转动的过程中,这两把三角尺除了AB∥CE外,是否还存在互相平行的边?若存在,请直接写出平行时三角尺ABC所有可能转过的度数(不必说明理由);若不存在,请说明理由.
四、综合题
-
16. 如图1,ADBC , ∠BAD的平分线交BC于点G , ∠BCD=90°.
 (1)、如图1,若∠ABG=48°,∠BCD的平分线交AD于点E、交射线GA于点F . 求∠AFC的度数;(2)、如图2,线段AG上有一点P , 满足∠ABP=3∠PBG , 若在直线AG上取一点M , 使∠PBM+∠DAG=90°,求的值.17. 如图,直线 , 直线与 , 分别交于点 , . 小安将直角三角板( , )按如图1放置,使点分别在直线上,且 .
(1)、如图1,若∠ABG=48°,∠BCD的平分线交AD于点E、交射线GA于点F . 求∠AFC的度数;(2)、如图2,线段AG上有一点P , 满足∠ABP=3∠PBG , 若在直线AG上取一点M , 使∠PBM+∠DAG=90°,求的值.17. 如图,直线 , 直线与 , 分别交于点 , . 小安将直角三角板( , )按如图1放置,使点分别在直线上,且 . (1)、填空:(填“”“”或“=”).(2)、如图2,的平分线交直线于点 .
(1)、填空:(填“”“”或“=”).(2)、如图2,的平分线交直线于点 .①当时,求的度数;
②小安将三角板沿直线左右移动,保持 , 点分别在直线和直线上移动,请直接写出的度数(用含的式子表示).