2023-2024学年湘教版初中数学七年级下学期 4.3 平行线的性质同步分层训练基础题
试卷更新日期：2024-03-26 类型：同步测试
一、选择题
-
1. 如图，直线DE∥FG，三角尺ABC的顶点B，C分别在DE，FG上.若∠BCF=25°，则∠ABE的度数为（ ）
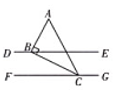A、25° B、55° C、65° D、75°2. 如图，直线a∥b，∠1=55°，则∠2的度数为 （ ）
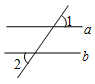A、35° B、45° C、55° D、125°3. 如图，直线 ， 直线与直线a相交于点P ， 与直线b相交于点Q ， 于点P ， 若 ， 则的度数为（ ）
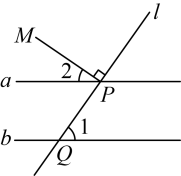A、 B、 C、 D、4. 如图，已知AB∥CD，则图中与∠1相等的角有（ ）
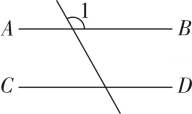A、5个 B、4个 C、3个 D、2个5. 光线在不同介质中的传播速度是不同的，因此当光线从水中射向空气时，要发生折射，由于折射率相同，所以在水中平行的光线，在空气中也是平行的．如图，的度数为（ ）
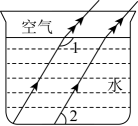A、 B、 C、 D、6. 如图，已知AB∥EG，BC∥DE，CD∥EF，则x，y，z三者之间的关系是 （ ）
A、x+y+z=180° B、x-z=y C、y-x=z D、y -x=x-z7. 如图， ， 的平分线与的平分线交于点 ， 当时，的度数为 （ ）
A、 B、 C、 D、8. 根据投影屏上出示的填空题，判断下列说法正确的是 （ ）已知：如图是△ABC.
试说明：∠BAC+∠B+∠C=180°.
解：过点A作DE∥ ◎ .
∴∠DAB=∠B，∠EAC= ＠ .
又∵∠DAB+∠BAC+∠EAC= ▲ .
∴ ※ +∠BAC+∠C=180°.
A、◎代表 AB B、@代表∠BAC C、▲代表 90° D、※代表∠B二、填空题
-
9. 如图，已知AB∥CD，∠2：∠3=1：2，则∠1=°．
10. 如图，由AB∥CD，可得∠B+=180°，理由是
11. 如图，已知AB∥CD，点E，F分别在AB，CD上，点G，H在两条平行线之间，∠AEG和∠GHF的平分线相交于点M.C若∠EGH=82°，∠HFD=20°，则∠M的度数为°.
12. 如图，点E，O，F 在同一条直线上，若AB∥EO，OF∥CD，则∠2+∠3-∠1=°.
13. 如图1所示为一架消防云梯，它由救援台 AB、延展臂BC(点B在点C 的左侧)、伸展主臂CD、支撑臂EF 构成，在作业过程中，救援台 AB、车身GH 及地面MN 三者始终保持水平.现为参与一项高空救援工作，需要进行作业调整，如图2，使得延展臂 BC 与支撑臂 EF 所在直线互相垂直，且∠EFH=69°，则这时∠ABC=°.
三、解答题
-
14. 如图1，直线a，b所成的角跑到画板外面去了，有什么办法量出这两条直线所成的角的度数?
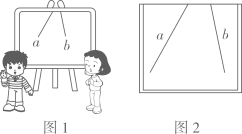(1)、请在图2的画板上画出你的测量方案图，并做简要说明.(2)、写出该画法依据的定理：15. 三角尺是学习数学的重要工具，将一副三角尺（∠A=60°，∠D=30°，∠B=∠E=45°）的直角顶点C按如图所示的方式叠放在一起，且∠ACE<90°，点E在直线AC 的上方，解决下列问题：
(1)、①若∠DCE=45°，求∠ACB的度数.②若∠ACB=140°，求∠DCE的度数.
(2)、由（1）猜想∠ACB 与∠DCE的数量关系，并说明理由.(3)、这两块三角尺是否存在一组边互相平行？ 若存在，请直接写出∠ACE的所有可能的值；若不存在，请说明理由.四、综合题
-
16. 已知：点C是∠AOB的OA边上一点（点C不与点O重合），点D是∠AOB内部一点，射线CD不与OB相交．
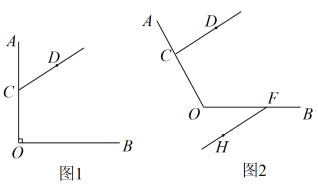(1)、如图1，∠AOB＝90°，∠OCD＝120°，过点O作射线OE，使得OE//CD．（其中点E在∠AOB内部）．①依据题意，补全图1；
②直接写出∠BOE的度数．
(2)、如图2，点F是射线OB上一点，且点F不与点O重合，当时，过点F作射线FH，使得FH//CD（其中点H在∠AOB的外部），用含的代数式表示∠OCD与∠BFH的数量关系，并证明．17. 已知一个角的两边与另一个角的两边分别平行，请结合图形回答下列问题：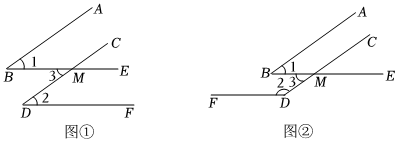
(1)、如图 ， ， ， 直接写出与的关系 ；(2)、如图 ， ， ， 猜想与的关系，并说明理由；(3)、由（1）（2），我们可以得出结论：一个角的两边与另一个角的分别平行，那么这两个角 ；(4)、应用：两个角的两边分别平行，且一个角比另一个角的倍少 ， 求出这两个角的度数分别是多少度？