湘教版初中数学七年级下学期 4.1.2 相交直线所成的角同步分层训练培优题
试卷更新日期:2024-03-26 类型:同步测试
一、选择题
-
1. 如图,直线、相交于点 , 平分 , 若 , 则的度数是( )
 A、 B、 C、 D、2. 如图,直线AB , CD相交于点O , OE平分∠AOC , 若∠BOD=70°,则∠DOE的度数是( )
A、 B、 C、 D、2. 如图,直线AB , CD相交于点O , OE平分∠AOC , 若∠BOD=70°,则∠DOE的度数是( ) A、70° B、35° C、120° D、145°3. 如图,∠1和∠2不是同位角的是( )A、
A、70° B、35° C、120° D、145°3. 如图,∠1和∠2不是同位角的是( )A、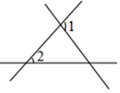 B、
B、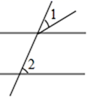 C、
C、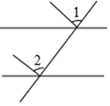 D、
D、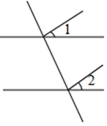 4. 如图,直线AB,CD相交于点O,若 , , 则的度数为( )
4. 如图,直线AB,CD相交于点O,若 , , 则的度数为( ) A、30° B、50° C、60° D、80°5. 下列选项中,∠1和∠2是对顶角的是( ).A、
A、30° B、50° C、60° D、80°5. 下列选项中,∠1和∠2是对顶角的是( ).A、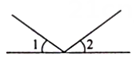 B、
B、 C、
C、 D、
D、 6. 如图,直线、、相交于点 , 且 , 平分 , 若 , 则的度数为( )
6. 如图,直线、、相交于点 , 且 , 平分 , 若 , 则的度数为( )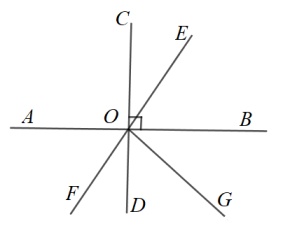 A、 B、 C、 D、无法确定7. 如图,已知两条直线被第三条直线所截,则下列说法正确的是( )
A、 B、 C、 D、无法确定7. 如图,已知两条直线被第三条直线所截,则下列说法正确的是( ) A、∠1与∠2是对顶角 B、∠2与∠5是内错角 C、∠3与∠7是同位角 D、∠3与∠8是同旁内角8. 平面上三条直线两两相交最多能构成对顶角的对数是( ).A、7 B、6 C、5 D、4
A、∠1与∠2是对顶角 B、∠2与∠5是内错角 C、∠3与∠7是同位角 D、∠3与∠8是同旁内角8. 平面上三条直线两两相交最多能构成对顶角的对数是( ).A、7 B、6 C、5 D、4二、填空题
-
9. 如图,两条直线相交于点O , 若 , 则度.
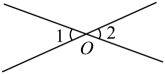 10. 若两条直线相交所成的四个角中,有两个角分别是(7x- 80)°和(100-2x)°,则x=11. 如图,直线AB与直线CD相交于点O, , 则 .
10. 若两条直线相交所成的四个角中,有两个角分别是(7x- 80)°和(100-2x)°,则x=11. 如图,直线AB与直线CD相交于点O, , 则 . 12. 观察下列各图,寻找对顶角(不含平角).如图1,图中有2条直线相交,则对顶角有对;如图2,图中有3条直线相交于一点,则对顶角有对;如图3图中有条直线相交于一点,则对顶角有对.
12. 观察下列各图,寻找对顶角(不含平角).如图1,图中有2条直线相交,则对顶角有对;如图2,图中有3条直线相交于一点,则对顶角有对;如图3图中有条直线相交于一点,则对顶角有对. 13. 如图
13. 如图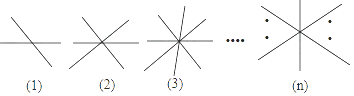
( 1 )两条直线相交于一点有2组不同的对顶角;
( 2 )三条直线相交于一点有6组不同的对顶角;
( 3 )四条直线相交于一点有12组不同的对顶角;
( 4 )n条直线相交于同一点有组不同对顶角.(如图所示)
三、解答题
-
14. 如图所示,直线a,b,c两两相交,∠1=2∠3,∠2=65°,求∠4的度数.
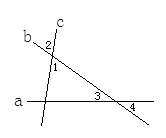 15. 复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
15. 复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想. (1)、如图1,直线l1 , l2被直线l3所截,在这个基本图形中,形成了对同旁内角.(2)、如图2,平面内三条直线l1 , l2 , l3两两相交,交点分别为A、B、C,图中一共有对同旁内角.(3)、在同一平面内四条直线两两相交,最多可以形成对同旁内角.(4)、在同-平面内n条直线两两相交,最多可以形成对同旁内角.
(1)、如图1,直线l1 , l2被直线l3所截,在这个基本图形中,形成了对同旁内角.(2)、如图2,平面内三条直线l1 , l2 , l3两两相交,交点分别为A、B、C,图中一共有对同旁内角.(3)、在同一平面内四条直线两两相交,最多可以形成对同旁内角.(4)、在同-平面内n条直线两两相交,最多可以形成对同旁内角.四、综合题
-
16. 在下列各图中,点O为直线AB上一点,∠AOC=60°
 (1)、如图1,三角板一边OM在射线OB上,另一边ON在直线AB的下方,则∠BOC的度数°,∠CON的度数为°;(2)、如图2,三角板一边OM恰好在∠BOC的角平分线OE上,另一边ON在直线AB的下方,此时∠BON的度数为;(3)、在图2中,延长线段NO得到射线OD,如图3,则AOD的度数为°;∠DOC与∠BON的数量关系是∠DOC ∠BON.(填“>”、“=”或“<”).17. 对于复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零,这是一种常见的数学解题思想.
(1)、如图1,三角板一边OM在射线OB上,另一边ON在直线AB的下方,则∠BOC的度数°,∠CON的度数为°;(2)、如图2,三角板一边OM恰好在∠BOC的角平分线OE上,另一边ON在直线AB的下方,此时∠BON的度数为;(3)、在图2中,延长线段NO得到射线OD,如图3,则AOD的度数为°;∠DOC与∠BON的数量关系是∠DOC ∠BON.(填“>”、“=”或“<”).17. 对于复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零,这是一种常见的数学解题思想. (1)、如图1.直线l1、l2被直线l3所截,在这个基本图形中,形成了对同旁内角.(2)、如图2.平面内三条直线l1 , l2 , l3两两相交,交点分别为A,B,C,图中一共有对同旁内角.(3)、平面内四条直线两两相交,最多可以形成对同旁内角
(1)、如图1.直线l1、l2被直线l3所截,在这个基本图形中,形成了对同旁内角.(2)、如图2.平面内三条直线l1 , l2 , l3两两相交,交点分别为A,B,C,图中一共有对同旁内角.(3)、平面内四条直线两两相交,最多可以形成对同旁内角