2023-2024学年湘教版初中数学七年级下学期 4.1.1 相交与平行同步分层训练培优题

试卷更新日期：2024-03-26 类型：同步测试

进入出卷网下载

一、选择题

1. 在同一平面内有四条直线两两相交，可以有几个交点（）

A、6个或4个 B、1个或4个 C、1个或4个或6个 D、6个

查看试题解析
2. 经过直线 $a$ 外一点 $P$ 的5条不同的直线中，与直线 $a$ 相交的直线至少有（）

A、2条 B、3条 C、4条 D、5条

查看试题解析
3. 若直线a，b，c，d有下列关系，则推理正确的是（）

A、∵ $a ∥ b$ ， $b ∥ c$ ，

∴ $c ∥ d$
B、∵ $a ∥ c$ ， $b ∥ d$ ，

∴ $c ∥ d$
C、∵ $a ∥ b$ ， $a ∥ c$ ，

∴ $b ∥ c$
D、∵ $a ∥ b$ ， $c ∥ d$ ，

∴ $a ∥ c$

查看试题解析
4. 如图，直线 $l_{1}$ 与 $l_{2}$ 相交于点 $O$ ，对于平面内任意一点 $M$ ，点 $M$ 直线 $l_{1}$ ， $l_{2}$ 的距离分别为 $p$ ， $q$ ，则称有序实数对 $(p ， q)$ 是点 $M$ 的“距离坐标”，根据上述定义，“距离坐标”是 $(5 ， 3)$ 的点的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
5. 按下所语句画图：点M在直线a上，也在直线b上，但不在直线c上，直线a，b，c两两相交，下图中正确的是（）

A、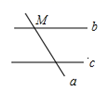 B、 C、 D、

查看试题解析
6. 若四条直线在平面内交点的个数为 $a$ ，则 $a$ 的可能取值有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
7. 两条直线最多有1个交点，三条直线最多有3个交点，四条直线最多有6个交点，那么六条直线最多有（）

A、21个交点 B、18个交点 C、15个交点 D、10个交点

查看试题解析
8. 在同一平面内，我们把两条直线相交将平面分得的区域数记为 $a_{1}$ ，三条直线两两相交最多将平面分得的区域数记为 $a_{2}$ ，四条直线两两相交最多将平面分得的区域数记为 $a_{3} ， \cdot \cdot \cdot ， (n + 1)$ 条直线两两相交最多将平面分得的区域数记为 $a_{n}$ ，若 $\frac{1}{a_{1} - 1} + \frac{1}{a_{2} - 1} + \cdot \cdot \cdot + \frac{1}{a_{n} - 1} = \frac{10}{11}$ ，则 $n =$ （）

A、 $10$ B、 $11$ C、 $20$ D、 $21$

查看试题解析

二、填空题

9. 如图，已知 $O M ∥ a$ ， $O N ∥ a$ ，所以点 $O 、 M 、 N$ 三点共线的理由.

查看试题解析
10. 如图，在直线a外有一点P，经过点P可以画无数条直线，如果 $a / / b$ ，那么过点P的其它直线与直线a一定不平行，理由是．

查看试题解析
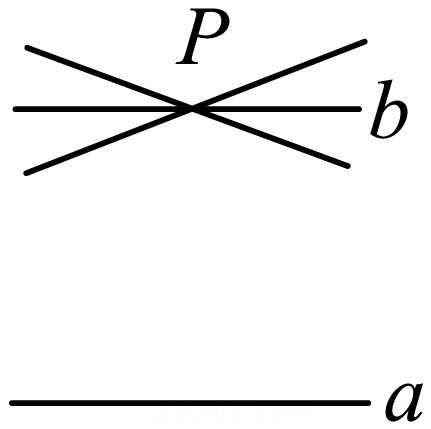11. 如图，在正方体中，与线段AB平行的线段有．

查看试题解析
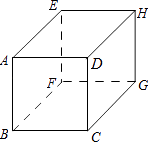12. 在同一平面内，两条直线相交时最多有1个交点，三条直线相交时最多有3个交点，四条直线相交时最多有6个交点，…，那么十条直线相交时最多有个交点．

查看试题解析
13. 在同一平面中，两条直线相交有一个交点，三条直线两两相交最多有3个交点，四条直线两两相交最多有6个交点……由此猜想，当相交直线的条数为n时，最多可有的交点数m与直线条数n之间的关系式为：m=.（用含n的代数式填空）

查看试题解析

三、解答题

14. 已知直线a∥b，b∥c，c∥d，则a与d的关系是什么？为什么？

查看试题解析
15. 在同一平面内三条直线交点有多少个？
甲：同一平面三直线相交交点的个数为0个，因为a∥b∥c，如图（1）所示．
乙：同一平面内三条直线交点个数只有1个，因为a，b，c交于同一点O，如图（2）所示．
以上说法谁对谁错？为什么？

查看试题解析

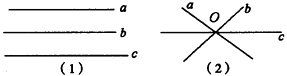
四、综合题

16. （原创题）如图所示，在书写艺术字时，常常运用画“平行线段”这种基本作图方法，此图是在书写字“M”：

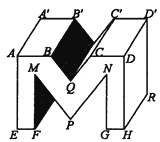(1)、请从正面，上面，右侧三个不同方向上各找出一组平行线段，并用字母表示出来；

(2)、EF与A′B′有何位置关系？CC′与DH有何位置关系？

查看试题解析
17. 课题学习：平行线的“等角转化”功能.

(1)、阅读理解：如图1，已知点A是 $B C$ 外一点，连接 $A B$ 、 $A C$ ，求 $∠ B + ∠ B A C + ∠ C$ 的度数.阅读并补充下面推理过程.
解：过点A作 $E D ∥ B C$ ，
$∴$ $∠ B =$ ▲ ， $∠ C$ ▲ ，
$∵$ $∠ E A B + ∠ B A C + ∠ D A C = 180 °$ ，
$∴$ $∠ B + ∠ B A C + ∠ C = 180 °$ .

(2)、方法运用：如图2，已知 $A B ∥ E D$ ，求 $∠ B + ∠ B C D + ∠ D$ 的度数；

(3)、深化拓展：已知 $A B ∥ C D$ ，点C在点D的右侧， $∠ A D C = 50 °$ ， $B E$ 平分 $∠ A B C$ ， $D E$ 平分 $∠ A D C$ ， $B E$ ， $D E$ 所在的直线交于点E，点E在直线 $A B$ 与 $C D$ 之间.
①如图3，点B在点A的左侧，若 $∠ A B C = 36 °$ ，求 $∠ B E D$ 的度数.
②如图4，点B在点A的右侧，且 $A B < C D$ ， $A D < B C$ .若 $∠ A B C = n °$ ，求 $∠ B E D$ 度数.（用含n的代数式表示）

查看试题解析