2023-2024学年湘教版初中数学七年级下学期 4.1.1 相交与平行同步分层训练基础题
试卷更新日期：2024-03-26 类型：同步测试
一、选择题
-
1. 在同一平面内，对两条直线可能的位置关系，描述最准确的是 （ ）A、平行 B、相交 C、平行或相交 D、平行、相交或垂直2. 已知直线AB和直线AB 外一点 P，过点 P作直线与AB 平行，这样的直线 （ ）A、有且只有一条 B、不止一条 C、不存在 D、不存在或只有一条3. 如图，点是直线外一点，过点分别作 ， ， 则点、、三个点必在同一条直线上，其依据是（ ）
A、两点确定一条直线 B、同位角相等，两直线平行 C、过直线外一点有且只有一条直线与这条直线平行 D、平行于同一条直线的两条直线平行4. 在数学课上，老师画一条直线a，按如图所示的方法，画一条直线b与直线a平行，再向上推三角尺，画一条直线c也与直线a平行，此时，发现直线b与直线c也平行，这就说明了（ ）
A、如果两条直线都和第三条直线平行，那么这两条直线也互相平行 B、两直线平行，同位角相等 C、同旁内角相等，两直线平行 D、过直线外一点，有且只有一条直线与已知直线5. 直线、线段、射线的位置如图所示，下图中能相交的是（ ）A、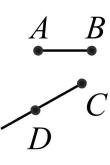
B、
C、
D、
6. 在同一平面内，有a，b，c三条直线，若a与b不平行，b与c不平行，则下列判断中，正确的是（ ）A、a与c一定平行 B、a与c一定不平行 C、a与c一定垂直 D、a与c可能相交，也可能平行7. 如图，经过直线a外一点O的4条直线中，与直线a相交的直线至少有（ ）
A、1条 B、2条 C、3条 D、4条8. 小红在“趣味数学”社团活动中探究了直线交点个数的问题．现有7条不同的直线ln(n=1，2，3，4，5，6，7)，其中l1、l2互相平行，l3、l4、I5三条直线交于一点，则他探究这7条直线的交点个数最多是（ ）A、17个 B、18个 C、19个 D、21个二、填空题
-
9. a，b，c为同一平面内三条不同的直线，若a⊥b，c⊥b，则a与c的位置关系是.10. 给下面的图形归类(图中的线均为直线)：
两条直线相交的是；两条直线互相平行的是(填序号)
11. 下列说法：两条不相交的直线叫平行线；
两条不相交的线段，在同一平面内必平行；
经过直线外一点有且只有一条直线与这条直线平行；
若直线 ， ， 那么 ，
其中错误的是 只填序号
12. 有下列说法：①在同一平面内，过直线外一点有且只有一条直线与已知直线平行；
②无论k取任何实数，多项式总能分解成两个一次因式积的形式；
③已知二元一次方程组的解也是二元一次方程的解，则a的值是2；
④若 ， ， 则；
其中正确的说法是.
13. 如图，这是顺义区第一座互通式立交桥——燕京桥，如果将顺平路和通顺路看做是两条直线，那么这两条直线的位置关系是 ．
①相交 ②不相交 ③平行 ④在同一平面内 ⑤不在同一平面内
三、解答题
-
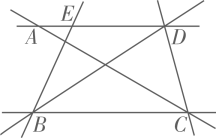
14. 如图所示，A、B、C、D、E五个城市，它们之间原有道路相通，现在打算在C、E两城市之间沿直线再修建一条公路，这条公路与原公路的交叉处必须设立交桥，问怎样确定立交桥的位置？应架设几座立交桥？
15. 有这样一个问题：在同一平面内，互不重合的三条直线的交点有多少个？下列是甲、乙两位同学的答案．甲：在同一平面内，互不重合的三条直线交点的个数为0，因为a∥b∥c．如图1所示．
乙：在同一平面内，互不重合的三条直线交点的个数为1，因为a，b，c交于同一点O，如图2所示．
以上说法谁对谁错？为什么？
四、综合题
-
16. 如图所示，在书写艺术字时，常常运用画“平行线段”这种基本作图方法，此图是在书写字母“M”：
(1)、请从正面，上面，右侧三个不同方向上各找出一组平行线段，并用字母表示出来；(2)、EF与A′B′有何位置关系，CC′与DH有何位置关系？17. 平面上有7条不同的直线，如果其中任何三条直线都不共点．(1)、请画出满足上述条件的一个图形，并数出图形中各直线之间的交点个数；(2)、请再画出各直线之间的交点个数不同的图形（至少两个）；(3)、你能否画出各直线之间的交点个数为n的图形，其中n分别为6，21，15？(4)、请尽可能多地画出各直线之间的交点个数不同的图形，从中你能发现什么规律？