2023-2024学年湘教版初中数学七年级下学期 3.3 公式法同步分层训练培优题

试卷更新日期：2024-03-26 类型：同步测试

进入出卷网下载

一、选择题

1. 下列各式中，能用平方差公式进行因式分解的是（）

A、 $x^{2} + 1$ B、 $x^{2} - 4$ C、 $x^{3} - 8$ D、 $x^{2} + 4 x + 1$

查看试题解析
2. 如果一个数等于两个连续奇数的平方差，那么我们称这个数为“幸福数”.下列数中，属于“幸福数”的是（）

A、205 B、250 C、502 D、520

查看试题解析
3. 某同学在因式分解时，不小心把等式x⁴-△=(x²+4)(x+2)(x-○)中的“△”，“○”处两个数弄污了，则代数式中的△，○分别对应的一组数应该是（）

A、8，1 B、16，2 C、24，3 D、64，8

查看试题解析
4. 给出下列各式： $x^{2} - y^{2}$ ， $- x^{2} + y^{2}$ ， $(- x)^{2} + (- y)^{2}$ ， $- x^{2} - y^{2}$ ， $x^{4} - y^{4}$ ，其中能用平方差公式进行因式分解的有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
5. 下列分解因式错误的是（　　）

A、y（x-y）+x（x-y）＝（x-y）（x+y） B、25x²-4y²＝（5x+2y）（5x-2y） C、4x²+20x+25＝（2x+5）² D、a²（a-b）-2a（a-b）+b²（a-b）＝（a-b）³

查看试题解析
6. 因式分解正确的是（　　）

A、-4a²+9b²=（-2a+3b）（2a+3b） B、x³-x=x（x²-1） C、（a+b）（a-b）=a²-b² D、m³+m²+m=m（m²+m）

查看试题解析
7. 计算3×（ ${(\frac{2018 - \sqrt{2018^{2} - 12 \times 2019}}{2 \times 3})}^{2}$ ﹣2018×（ $\frac{2018 - \sqrt{2018^{2} - 12 \times 2019}}{2 \times 3}$ ）+1的结果等于（　　）

A、﹣2017 B、﹣2018 C、﹣2019 D、2019

查看试题解析
8. 下列二次三项式在实数范围内不能因式分解的是（）

A、 $6 x^{2} + x - 15$ B、 $3 y^{2} + 7 y + 3$ C、 $x^{2} - 2 x - 4$ D、 $2 x^{2} - 4 x y + 5 y^{2}$

查看试题解析

二、填空题

9. 分解因式： $x^{2} - 16 y^{2} =$ ．

查看试题解析
10. 把多项式9x﹣x³分解因式的结果为．

查看试题解析
11. 如果多项式9x²+1加上一个单项式后，使它能成为一个多项式的平方，那么加上的多项式可以是(应写尽写)

查看试题解析
12. 分解因式： $x^{2} (a - b) + 4 y^{2} (b - a) =_{.}$

查看试题解析
13. 若 $| a + 2 | + a^{2} - 4 a b + 4 b^{2} = 0$ ，则 $a =$ ， $b =$ ．

查看试题解析

三、解答题

14. 从边长为a的正方形中剪掉一个边长为b的正方形(如图①)，然后将剩余部分拼成一个长方形(如图②).

(1)、上述操作能验证的等式是 ▲ ；

(2)、应用你从(1)得出的等式，完成下列各题：
①已知x²−4y²=12，x+2y=4，求x−2y的值.
②计算：(1− $\frac{1}{2^{2}}$ )(1− $\frac{1}{3^{2}}$ )(1− $\frac{1}{4^{2}}$ )…(1− $\frac{1}{1 9^{2}}$ )(1− $\frac{1}{2 0^{2}}$ )．

查看试题解析
15. 阅读材料： $a^{3} - b^{3} + a^{2} b - a b^{2} = (a^{3} + a^{2} b) - (b^{3} + a b^{2})$
$= a^{2} (a + b) - b^{2} (a + b)$
＝（ ▲ ） $= (a + b)$
＝ ▲ ．

(1)、请把阅读材料补充完整；

(2)、分解因式： $4 x^{2} - 2 x - y^{2} - y$ ；

(3)、已知 $a$ ， $b$ ， $c$ 为 $△ A B C$ 的三边长，若 $a^{2} + b^{2} + 2 c^{2} - 2 a c - 2 b c = 0$ ，试判断 $△ A B C$ 的形状，并说明理由．

查看试题解析

四、综合题

16. 在课后服务课上，老师准备了若干个如图1的三种纸片，A种纸片是边长为a的正方形，B种纸片是边长为b的正方形，C种纸片是长为b，宽为α的长方形，并用A种纸片一张，B种纸片一张，C种纸片两张拼成如图2的大正方形．

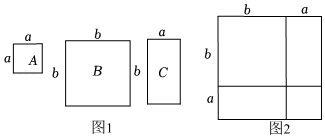(1)、根据图2，写出一个我们熟悉的数学公式．

(2)、根据（1）中的数学公式，解决如下问题：
①已知：a+b＝7，a²+b²＝25，求ab的值．
②如果一个长方形的长和宽分别为（8-x）和（x-2），且（8-x）²+（x-2）²＝20，求这个长方形的面积．

查看试题解析
17. 阅读理解：
对于二次三项式 $x^{2} + 2 a x + a^{2}$ ，能直接用公式法进行因式分解，得到 $x^{2} + 2 a x + a^{2} = {(x + a)}^{2}$ ，但对于二次三项式 $x^{2} + 2 a x - 8 a^{2}$ ，就不能直接用公式法了.

我们可以求用这样的方法：在二次三项式 $x^{2} +$ $2 a x - 8 a^{2}$ 中先加上一项 $a^{2}$ ，使其成为完全平方式，再减去 $a^{2}$ 这项，使整个式了的值不变，于是：

$x^{2} + 2 a x - 8 a^{2}$

$= x^{2} + 2 a x - 8 a^{2} + a^{2} - a^{2}$

$= x^{2} + 2 a x + a^{2} - 8 a^{2} - a^{2}$

$= (x^{2} + 2 a x + a^{2}) - (8 a^{2} + a^{2})$

$= {(x + a)}^{2} - 9 a^{2}$

$= (x + a + 3 a) (x + a - 3 a)$

$= (x + 4 a) (x - 2 a)$

像这样把二次三项式分解因式的方法叫做添(拆)项法.

(1)、问题解决：请用上述方法将二次三项式x²＋2ax—3a²分解因式；

(2)、拓展应用：二次三项式x²-4x＋5有最小值或最大值吗？如果有，请你求出来并说明理由.

查看试题解析