2023-2024学年湘教版初中数学八年级下学期 5.2 频数直方图同步分层训练提升题
试卷更新日期：2024-03-26 类型：同步测试
一、选择题
-
1. 在频数直方图中有 11个小长方形，若中间一个小长方形的面积等于其他 10个小长方形面积的和的一半，且数据总数为96，则中间一组的频数为（ ）A、32 B、0.5 C、48 D、0.332. 对某校600名学生的体重（kg）进行统计，得到如图所示的统计图（横轴上每组数据包含最小值不包含最大值），则学生体重在60kg及以上的人数为（ ）
A、120 B、150 C、180 D、3303. 观察如图所示的频数直方图，其中组界为99.5~124.5这一组的频数是（ ）
A、5 B、6 C、7 D、84. 小明同学对部分菲尔兹奖得主获奖时的年龄进行了统计，得到的频数直方图(每一组含前一个边界值，不含后一个边界值)如图所示，其中获奖时年龄在36岁及以上的有（ ）
A、13人 B、27人 C、33人 D、47人5. 小杰调查了本班同学的体重情况，并绘制成了频数直方图，下列结论中，错误的是（ ）
A、全班总人数为45 B、体重在50~55kg的人数最多 C、全班学生中体重最大的是65kg D、体重在60~65kg的人数占全班总人数的6. 某次考试中，某班的数学成绩统计图如图所示，下列说法错误的是（ ）
A、得分在70~80分之间的人数最多 B、该班的总人数为40 C、得分在90~100分之间的人数最少 D、不及格(<60分)人数是67. 小文同学统计了他所在小区居民每天微信阅读的时间，并绘制了直方图．①小文同学一共统计了60人；②每天微信阅读不足20分钟的人数有12人；③每天微信阅读30-40分钟的人数最多；④每天微信阅读0-10分钟的人数最少．根据图中信息，上述说法中正确的是（ ）
A、①②③④ B、①②③ C、②③④ D、③④8. 某次考试中，某班级的数学成绩统计图如下，下列说法错误的是（ ）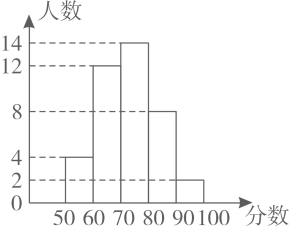
A、得分在90~100分之间的人数最少 B、该班的总人数为40 C、及格（≥60分）人数是26 D、得分在70~80分之间的人数最多二、填空题
-
9. 为了解某校1000名学生在进行家务劳动时对家用燃气设备安全知识的掌握情况，随机抽取100名学生参加问卷测试，将成绩进行整理得到频数直方图(每一组含前一个边界值，不含后一个边界值)如图所示，则该校成绩为 80分及以上的学生约有人.
10. 某养殖场对200头牲畜的质量进行统计，得到频数直方图(每一组含前一个边界值，不含后一个边界值)如图所示，其中质量在77.5kg及以上的牲畜有头.
11. 某校对名八年级学生身高进行统计，得到频数分布直方图每一组含前一个边界值，不含后一个边界值如图所示，其中身高在及以上的学生有人
12. 某校学生“亚运知识”竞赛成绩的频数分布直方图每一组含前一个边界值，不含后一个边界值如图所示，其中成绩在分及以上的学生有人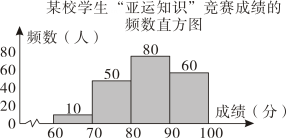
13. 根据某班40名学生身高的频数分布直方图（每组不含起点值，含终点值），回答下列问题：
(1)、人数最多的身高范围是；(2)、身高大于175cm的学生占全班人数的百分比是 ．三、解答题
-
14. 在太空种子种植体验实践活动中，为了解“字番2号”番茄，某校科技小组随机调查60株番茄的挂果数量x (单位：个)，并绘制如下不完整的统计图表：
“字番2号”番茄挂果数量统计表
挂果数量x(个)
频数(株)
频率
25≤x<35
6
0.1
35≤x<45
12
0.2
45≤x<55
a
0.25
55≤x<65
18
b
65≤x<75
9
0.15
请结合图表中的信息解答下列问题：
(1)、统计表中，a= ， b=(2)、将频数分布直方图补充完整．(3)、若绘制“番茄挂果数量扇形统计图”，则挂果数量在“35≤x<45”所对应扇形的圆心角度数为°(4)、若所种植的“字番2号”番茄有1000株，则可以估计挂果数量在“55≤x<65"范围的番茄有株．15. 第33届夏季奥林匹克运动会定于2024年7月26日在巴黎举行，某校七、八年级各有500名学生，为了解这两个年级学生对本次奥运会的关注程度，现从这两个年级各随机抽取n名学生进行奥运会知识测试，将测试成绩按以下六组进行整理（得分用x表示）：A：70≤x<75，B：75≤x<80，C：80≤x<85，
D：85<x<90， E：90≤x<95 ，F：95≤x<100.
根据得到的数据绘制七年级测试成绩频数直方图
和八年级测试成绩扇形统计图如图所示.
已知八年级测试成绩 D组的全部数据如下：
86，85，87，86，85，89，88.
请根据以上信息，完成下列问题：
(1)、n= ， a=.(2)、若测试成绩不低于 90分，则认定该学生对奥运会关注程度高，请估计该校七、八两个年级对奥运会关注程度高的学生总数.四、综合题
-
16. 为迎接杭州亚运会的召开，某校决定在全校范围内开展亚运知识的宣传教育活动为了了解宣传效果，随机抽取部分学生，并在活动前、后对这些学生进行了两次跟踪测评，两次测评中所有同学的成绩没有低于分，现在将收集的数据制成频数分布直方图每一组包含左端值，不包含右端值和频数表宣传活动后亚运知识成绩频数表：
成绩
频数
(1)、本次活动共抽取学生 ；(2)、宣传活动前，在抽取的学生中成绩人数最多一组的组中值是 分；(3)、表中的 ，宣传活动后，在抽取的学生中分数高于分的至少有 人，至多有 人；(4)、小聪认为，宣传活动后成绩在的人数为 ， 比活动前减少了人，因此学校开展的宣传活动没有效果请你结合统计图表，说一说小聪的看法是否正确为什么？17. 某中学积极推进校园文学创作，倡导每名学生每学期向校报编辑部至少投1篇稿件．学期末，学校对七、八年级的学生投稿情况进行调查．【数据的收集与整理】
分别从两个年级随机抽取相同数量的学生，统计每人在本学期投稿的篇数，制作了频数分布表．
投稿篇数（篇）
1
2
3
4
5
七年级频数（人）
7
10
15
12
6
八年级频数（人）
2
10
13
21
4
【数据的描述与分析】
(1)、求扇形统计图中圆心角的度数，并补全频数直方图．
(2)、根据频数分布表分别计算有关统计量：统计量
中位数
众数
平均数
方差
七年级
3
3
1.48
八年级
m
n
3.3
1.01
直接写出表格中m、n的值，并求出 ．
(3)、【数据的应用与评价】从中位数、众数、平均数、方差中，任选两个统计量，对七、八年级学生的投稿情况进行比较，并做出评价．