2023-2024学年湘教版初中数学八年级下学期 5.1 频数与频率同步分层训练培优题

试卷更新日期：2024-03-26 类型：同步测试

进入出卷网下载

一、选择题

1. 一次跳远比赛中，成绩在3m以上的有8人，频率为0.4，则参加比赛的共有（）

A、40人 B、30人 C、20人 D、10人

查看试题解析
2. 德惠某中学对八年级（2）班50名同学的一次数学测试成绩进行统计，其中80.5~90.5分这一组的频数是18，那么这个班的学生这次数学测试成绩在80.5~90.5分之间的频率是（）

A、18 B、0.36 C、18% D、0.9

查看试题解析
3. 实数0， $\sqrt{2}$ ， -π，0.1010010001…… $\frac{22}{7}$ 其中无理数出现的频率是（）

A、20% B、40% C、60% D、80%

查看试题解析
4. 已知一组数据10，8，6，10，9，13，11，11，10，10，下列各组中频率为0.2的是（）

A、5.5~7.5 B、7.5~9.5 C、9.5~11.5 D、11.5~13.5

查看试题解析
5. 给出下面一组数据：19，20，25，31，28，27，26，21，20，22，24，23，25，29，27，28，27，30，18，20.若组距为2，则这组数据应分成（）组.

A、4 B、5 C、6 D、7

查看试题解析
6. 新型冠状病毒（Novel Coronavirus），其中字母“v”出现的频数和频率分别是（　　）

A、2； $\frac{1}{16}$ B、2； $\frac{1}{8}$ C、4； $\frac{1}{8}$ D、4； $\frac{1}{4}$

查看试题解析
7. 已知一组数据： $π$ ， $- \frac{2}{3}$ ， 0.1010010001， $- \frac{\sqrt{3}}{2}$ ， $0 . \dot{2}$ ，其中无理数出现的频数是（）

A、2 B、3 C、4 D、5

查看试题解析
8. “俭以养德”是中华民族的优秀传统，时代中学为了对全校学生零花钱的使用进行符合题意引导，随机抽取50名学生，对他们一周的零花钱数额进行了统计，并根据调查结果绘制了不完整的频数分布表和扇形统计图，如图所示：
组别
零花钱数额 $x$ /元
频数
一
$x \leq 10$
二
$10 < x \leq 15$
12
三
$15 < x \leq 20$
15
四
$20 < x \leq 25$
$a$
五
$x > 25$
5
关于这次调查，下列说法正确的是（）

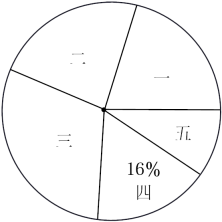A、总体为50名学生一周的零花钱数额 B、五组对应扇形的圆心角度数为36° C、在这次调查中，四组的频数为6 D、若该校共有学生1500人，则估计该校零花钱数额不超过20元的人数约为1200人

查看试题解析

二、填空题

9. 在一个不透明的布袋中，有红球、黑球、白球共60个，它们除颜色外其他都相同．小明从中任意摸出一个球，查看色后放回并摇匀，通过多次摸球试验后，发现摸到红球、黑球的频率分别稳定在0.15和0.45，则他估计布袋中白球的个数约是个．

查看试题解析
10. 如图是第19届亚运会的宣传画，总面积为4m² ，现将宣传画平铺在地上，向宣传画内随机投掷骰子（假设骰子落在宣传画内的每一点都是等可能的），经过大量重复投掷试验，发现骰子落在宣传画的图案上的频率稳定在常数0.7附近，由此可估计宣传画上图案的面积约为 m² ．

查看试题解析
11. 在某公益活动中，小明对本年级50名同学的捐款情况进行了统计，因缺失部分数据，得到了不完整的统计图，则本次捐款20元的人数有名.

查看试题解析
12. 某中学抽取部分学生对“你最喜欢的球类运动”调查问卷，收集整理数据后，列频数分部表 $($ 部分 $)$ 如下：
项目
乒乓球
羽毛球
篮球
足球
频数
          $40$
          $25$
          $m$
百分比
          $40 %$
          $25 %$
          $n$
则 $m n$ 的值为．

查看试题解析

三、解答题

13. 已知某月在某医院出生的20名新生婴儿的体重如下(单位： kg)
4.7，2.9，3.2，3.5，3.8，
3.4，2.8，3.3，4.0，4.5，
3.6，4.8，4.3，3.6，3.4，
3.5，3.6，3.5，3.7，3.7．

(1)、若以0.4kg为组距，对这组数据进行分组，应分成几组？

(2)、一般新生婴儿的正常体重在2.5~4.0kg之间(包括2.5kg和4.0kg)，求体重在正常范围内的婴儿所占的百分比．

查看试题解析
14. 为弘扬红色文化，传颂红色故事，延安革命老区某学校在八年级开展了红色文化知识竞赛活动，并随机抽取了20名参赛选手的成绩（竞赛成绩均为正数，满分100分）进行统计分析.随机抽取的成绕如下：77，86，80，76，79，100，95，80，75，90，94，86，68，95，88，78，90，82，86，100，整理数据：
分数/分
$60 < x ⩽ 70$
$70 < x ⩽ 80$
$80 < x ⩽ 90$
$90 < x ⩽ 100$
人数/人
2
a
b
5
根据以上信息回答下列问题：

(1)、填空： $a =$ ， $b =$ .

(2)、这20名参赛人员成绩的众数为分，中位数为分；

(3)、小李的参赛成绩为88分，你认为他的成绩属于“中上”水平吗?请说明理由.

查看试题解析

四、综合题

15. 教育部办公厅在《关于进一步加强中小学生体质健康管理工作的通知》中明确要求保障学生每天校内、校外各1小时体育活动时间．某校为了解本校九年级学生每天参加体育活动的情况，随机抽取了

n

名学生，对某一天的体育活动时间进行了调查，根据调查结果绘制了如下不完整的频数分布表和扇形统计图．

调查结果的频数分布表

组别	时间 $t$ （分钟）	频数
$A$	$30 \leq t < 60$	5
$B$	$60 \leq t < 90$	$a$
$C$	$90 \leq t < 120$	$b$
$D$	$120 \leq t < 150$	12
$E$	$t \geq 150$	8

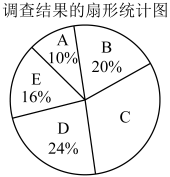
根据上述信息，解答下列问题：

(1)、频数分布表中的

a =

，扇形统计图中

C

组所在的扇形的圆心角为度；

(2)、被抽取的

n

名学生这一天的体育活动时间数据的中位数在哪一组（直接写出组别即可）；

(3)、若该校九年级共有720名学生，试估计该校九年级学生平均每天体育活动时间不低于120分钟的学生人数．

查看试题解析

16. 为了解我国2022年25个地区第一季度快递业务收入情况，收集了这25个地区第一季度快递业务收入（单位：亿元）的数据，并对数据进行了整理、描述和分析，给出如下信息．
a．排在前5位的地区第一季度快递业务收入的数据分别为：
5349  437.0  270.3  187.7  104.0
b．其余20个地区第一季度快递业务收入的数据的频数分布表如下：
快递业务收入x
$0 \leq x < 20$
$20 \leq x < 40$
$40 \leq x < 60$
$60 \leq x \leq 80$
频数
6
10
1
3
c．第一季度快递业务收入的数据在 $20 \leq x < 40$ 这一组的是：
20.2  20.4  22.4  24.2  26.1  26.5  28.5  34.4  39.1  39.8
d．排在前5位的地区、其余20个地区、全部25个地区第一季度快递业务收入的数据的平均数、中位数如下：

前5位的地区
其余20个地区
全部25个地区
平均数
306.8
29.9
n
中位数
270.3
m
28.5
根据以上信息，回答下列问题：

(1)、表中m的值为；

(2)、在下面3个数中，与表中n的值最接近的是（填写序号）；
①30           ②85       ③150

(3)、根据（2）中的数据，预计这25个地区2022年全年快递业务收入约为亿元．

查看试题解析
17. 某学校组织了“热爱宪法，捍卫宪法”的知识竞赛，赛后发现所有学生的成绩（总分100分）均不低于50分，为了解本次竞赛的成绩分布情况，随机抽取若干名学生的成绩作为样本进行整理，并绘制了不完整的统计图表，请你根据统计图表解答下列问题．
学校若干名学生成绩分布统计表
分数段（成绩为x分）
频数
频率
50≤x＜60
16
0.08
　60≤x＜70
a
0.31
　70≤x＜80
72
0.36
　80≤x＜90
c
d
　90≤x≤100
12
b

(1)、此次抽样调查的样本容量是　　；

(2)、写出表中的a＝　　， b＝　　， c＝　　；

(3)、补全学生成绩分布直方图；

(4)、比赛按照分数由高到低共设置一、二、三等奖，若有25%的参赛学生能获得一等奖，则一等奖的分数线是多少？

查看试题解析

组别	零花钱数额 $x$ /元	频数
一	$x \leq 10$
二	$10 < x \leq 15$	12
三	$15 < x \leq 20$	15
四	$20 < x \leq 25$	$a$
五	$x > 25$	5

项目	乒乓球	羽毛球	篮球	足球
频数	$40$	$25$	$m$
百分比	$40 %$		$25 %$	$n$

分数/分	$60 < x ⩽ 70$	$70 < x ⩽ 80$	$80 < x ⩽ 90$	$90 < x ⩽ 100$
人数/人	2	a	b	5

快递业务收入x	$0 \leq x < 20$	$20 \leq x < 40$	$40 \leq x < 60$	$60 \leq x \leq 80$
频数	6	10	1	3

	前5位的地区	其余20个地区	全部25个地区
平均数	306.8	29.9	n
中位数	270.3	m	28.5

分数段（成绩为x分）	频数	频率
50≤x＜60	16	0.08
60≤x＜70	a	0.31
70≤x＜80	72	0.36
80≤x＜90	c	d
90≤x≤100	12	b