2023-2024学年湘教版初中数学八年级下学期 4.5 一次函数的应用同步分层训练提升题

试卷更新日期：2024-03-26 类型：同步测试

进入出卷网下载

一、选择题

1. 一支签字笔的单价为2.5元，小涵同学拿了100元钱去购买了 $x (x \leq 40)$ 支该型号的签字笔，写出所剩余的钱 $y$ 与 $x$ 间的关系式是（）

A、 $y = 2.5 x$ B、 $y = 100 - 2.5 x$ C、 $y = 2.5 x - 100$ D、 $y = 100 + 2.5 x$

查看试题解析
2. 市自来水公司为鼓励居民节约用水，采取月用水量分段收费办法，某户居民应交水费y(元)与用水量x(吨)的函数关系如图，若该用户本月用水21吨，则应交水费（）

A、52.5元 B、48方 C、45元 D、42元

查看试题解析
3. 某品牌的自行车链条每节长为 $2.5 c m$ ，每两节链条相连部分重叠的圆的直径为 $0.8 c m$ ，按照这种连接方式， $n$ 节链条总长度为 $y c m$ ，则 $y$ 与 $n$ 的关系式是（）

A、 $y = 2.5 n$ B、 $y = 1.7 n$ C、 $y = 1.7 n + 0.8$ D、 $y = 2.5 n - 0.8$

查看试题解析
4. 皮克定理是格点几何学中的一个重要定理，它揭示了以格点为顶点的多边形的面积 $S = N + \frac{1}{2} L - 1$ ，其中 $N ， L$ 分别表示这个多边形内部与边界上的格点个数．在平面直角坐标系中，横、纵坐标都是整数的点为格点．已知 $A (0 ， 30)$ ， $B (20 ， 10) ， O (0 ， 0)$ ，则 $△ A B O$ 内部的格点个数是（）

A、266 B、270 C、271 D、285

查看试题解析
5. 甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶 $2 h$ ，并且甲车途中休息了 $0.5 h$ ，如图是甲、乙两车行驶的距离 $y (km)$ 与时间 $x (h)$ 的函数图象，有以下结论：
① $m = 1$ ；② $a = 40$ ；③甲车从A地到B地共用了7小时；④当两车相距 $50 km$ 时，乙车用时为 $\frac{1}{4} h$ .其中正确结论的个数是（）.

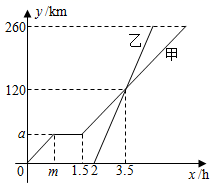A、4 B、3 C、2 D、1

查看试题解析
6. 2023年杭州亚运会竞赛项目中，有一个中华民族传统运动项目一一赛龙舟，此项比赛共分为六个小项目，中国健儿成绩骄人，共获得五金一银.在500米直道竞速赛道上，甲、乙两队所划行的路程y（单位：米）与时间t（单位：分）之间的函数关系如图所示，根据图中提供的信息，有下列说法：①甲队比乙队提前0.5分钟到达终点；②当划行1分钟时，甲队比乙队落后50米；③当划行 $\frac{5}{3}$ 分钟时，甲队追上乙队；④当甲队追上乙队时，两队划行的路程都是300米.其中错误的是（）

A、① B、② C、③ D、④

查看试题解析
7. 某市政府决定实施“煤改气”供暖改造工程，现甲、乙两工程队分别同时开挖两条600米长的管道，挖掘的管道长度y（米）与挖掘时间x（天）之间的关系如图所示，则下列说法中：
①甲队每天挖100米。②乙队开挖两天后，每天挖50米。③当 $x = 4$ 时，甲、乙两队所挖管道长度相同。④甲队比乙队提前2天完成任务。正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8.
甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示．则下列结论：
①A，B两城相距300千米；
②乙车比甲车晚出发1小时，却早到1小时；
③乙车出发后2.5小时追上甲车；
④当甲、乙两车相距50千米时，t= $\frac{5}{4}$ 或 $\frac{15}{4}$ ．
其中正确的结论有（　　）

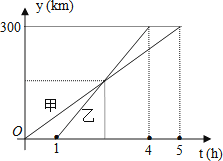A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 某品牌鞋子的长度ycm与鞋子的“码”数x之间满足一次函数关系．若22码鞋子的长度为16cm，44码鞋子的长度为27cm，则38码鞋子的长度为cm．

查看试题解析
10.
如图，直线y= $\sqrt{3}$ x，点A₁坐标为（1，0），过点A₁作x轴的垂线交直线于点B₁ ，以原点O为圆心，OB₁长为半径画弧交x轴于点A₂；再过点A₂作x轴的垂线交直线于点B₂ ，以原点O为圆心，OB₂长为半径画弧交x轴于点A₃ ， …，按此做法进行下去，点A_n的坐标为

查看试题解析
11. 某种大米的单价是5元/千克．当购买x千克大米时，花费为y元，则y关于x的函数表达式是.

查看试题解析
12. 某商店今年6月初销售纯净水的数量如下表：
日期
1
2
3
4
数量（瓶）
120
125
130
135
观察此表，利用所学函数知识预测今年6月7日该商店销售纯净水的数量约为瓶．

查看试题解析
13. 某医药研究所开发了一种新药，在实验药效时发现，如果成人按规定剂量服用，每毫升血液中含药量y（微克）随时间x（时）的变化情况如图所示，那么当成人按规定剂量服药后，根据图象回答下列问题：

(1)、服药后小时，血液中含药量最高，达每毫升微克，接着逐步衰减．

(2)、服药后5小时，血液中含药量为每毫升微克．

(3)、当x≤2时，y关于x的函数表达式是

(4)、当2≤x≤8时，y关于x的函数表达式是．

(5)、如果每毫升血液中含药量为3微克或3微克以上时治疗疾病最有效，那么这个有效时间范围是时．

查看试题解析

三、解答题

14. 经验表明，树在一定的成长阶段，其胸径(树的主干在地面以上1.3m处的直径)越大，树就越高.通过对某种树进行测量研究，发现这种树的树高y(m)是其胸径x(m)的一次函数.已知这种树的胸径为0.2m时，树高为20m；这种树的胸径为0.28m时，树高为22m.

(1)、求y与x之间的函数表达式.

(2)、当这种树的胸径为0.3m时，其树高是多少?

查看试题解析
15. 为迎接党的二十大，助力乡村振兴，实现群众增产增收，某商场设立专柜，在乡村地区直接采购农副产品，架起对口农户与消费者之间的桥梁，实现农副产品直产直销．该专柜负责人欲查询两种商品的进货数量，发现进货单已被墨水污染．
进货单
商品
进价/（元/件）
数量/件
金额/元
绩溪山核桃
45
黄山毛峰
75
商品采购员李经理对采购情况回忆如下：两种商品共采购了100件．

(1)、若采购花费的总金额为5700元，问绩溪山核桃和黄山毛峰的进货数量分别为多少？

(2)、在进价不变的情况下，由于市场火爆，该专柜负责人计划再次安排采购这两种商品共100件，假设黄山毛峰的进货数量为x（件），所花费的总金额为y（元）．
①求出y与x的函数关系式；
②若李经理用不超过5000元采购这两种商品，问他最多能购买黄山毛峰多少件？

(3)、若绩溪山核桃每件的售价为80元，黄山毛峰每件的售价为100元，商场规定黄山毛峰的进货数是为a（35≤a≤40）件，请问应怎样进货才能使商场在销售完这批货物时获利最多？此时利润为多少元？

查看试题解析

四、综合题

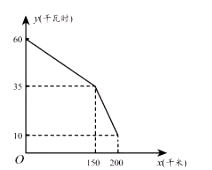
16. 如图是某型号新能源纯电动汽车充满电后，蓄电池剩余电量 $y$ （千瓦时）关于已行驶路程 $x$ （千米）的函数图象.

(1)、根据图象，直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程，当 $0 \leq x \leq 150$ 时，求1千瓦时的电量汽车能行驶的路程；

(2)、当 $150 \leq x \leq 200$ 时求 $y$ 关于 $x$ 的函数表达式，并计算当汽车已行驶180千米时，蓄电池的剩余电量.

查看试题解析
17. 兄妹俩放学后沿图1中的马路从学校出发，到书吧看书后回家.哥哥步行先出发，途中速度保持不变：妹妹骑车，到书吧前的速度为200米/分.图2中的图象分别表示两人离学校的路程s（米）与哥哥离开学校的时间t（分）的函数关系.

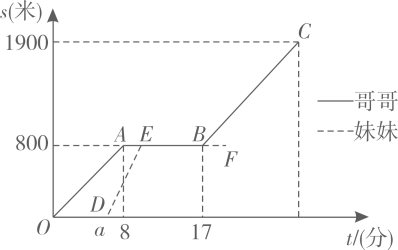(1)、求哥哥步行的速度.

(2)、已知妹妹比哥哥迟2分钟到书吧.
①求图中a的值；
②妹妹在书吧待了10分钟后回家，速度是哥哥的1.6倍，能否在哥哥到家前追上哥哥？若能，求追上时兄妹俩离家还有多远；若不能，说明理由.

查看试题解析

商品	进价/（元/件）	数量/件	金额/元
绩溪山核桃	45
黄山毛峰	75

日期	1	2	3	4
数量（瓶）	120	125	130	135