2023-2024学年湘教版初中数学八年级下学期 4.4 用待定系数法确定一次函数表达式同步分层训练培优题

试卷更新日期：2024-03-26 类型：同步测试

进入出卷网下载

一、选择题

1. 已知点（﹣2，m），（1，n）都在直线y＝2x+b上，则m，n的大小关系是（）

A、m＞n B、m＝n C、m＜n D、不能确定

查看试题解析
2. 关于一次函数y＝2x﹣3，下列说法正确的是（）

A、图象经过点（2，﹣1） B、图象经过第二象限 C、图象与x轴交于点（﹣3，0） D、函数值y随x的增大而增大

查看试题解析
3. 已知一次函数：y= - mx +n 的图象经过第二、三、四象限，则化简 $\sqrt{{(m - n)}^{2}} + \sqrt{n^{2}}$ 的结果是（）

A、n B、-m C、2m—n D、m-2n

查看试题解析
4. 如图，是一次函数y＝kx+b+1的图象，则下列结论正确的是（　　）

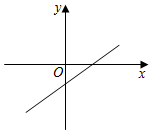A、k＜0，b＜0 B、k＞0，b＜﹣1 C、k＞0，b＜0 D、k＜0，b＞﹣1

查看试题解析
5. 如图，直角坐标系中有矩形AOBC，其中点A（-2，0），B（0，1），O是原点.若正比例函数y=kx（k≠0）的图象经过点C，则k的值为（）

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、-2 D、2

查看试题解析
6. 若 $A (x_{1} ， y_{1}) ， B (x_{2} ， y_{2})$ 是一次函数 $y = a x$ $+ 2 x - 2$ 图象上的不同的两点，记 $m = (x_{1}$ $- x_{2}) (y_{1} - y_{2})$ ，则当 $m > 0$ 时， $a$ 的取值范围是（）

A、 $a < 0$ B、 $a > 0$ C、 $a < - 2$ D、 $a > - 2$

查看试题解析
7. 对于函数 $y = - 5 x + 1$ ，下列结论：①它的图象必经过点 $(- 1 ， 5)$ ②它的图象经过第一、二、四象限 ③当 $x > 1$ 时， $y < 0$ ④ $y$ 的值随 $x$ 值的增大而增大，其中正确的个数有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
8. 如图，直线 $y = - \frac{3}{4} x + 6$ 分别与x轴、y轴交于点A、B，点C在线段 $O A$ 上，线段 $O B$ 沿 $B C$ 翻折．点O落在 $A B$ 边上的点D处．以下结论：① $A B = 10$ ；②直线 $B C$ 的解析式为 $y = - 2 x + 6$ ；③点 $D (\frac{24}{5} ， \frac{12}{5})$ ；④若线段 $B C$ 上存在一点P，使得以点P、O、C、D为顶点的四边形为菱形，则点P的横坐标是 $\frac{9}{5}$ ．以上所有结论中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

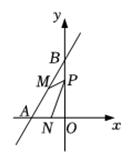
9. 一次函数y＝(2m－6)x＋5中，y随x的增大而减小，则m的取值范围是．

查看试题解析
10. 已知一次函数y=kx+b的图象经过点（1，3），（-1，2），则k²-b²=.

查看试题解析
11. 设函数满足以下两个条件：①图象过点 $(1 ， - 1)$ ；②当 $x > 1$ 时， $y$ 随 $x$ 增大而增大.则满足条件的函数表达式可以是(写出一个即可).

查看试题解析
12. 如图，直线 $y = 2 x + 4$ 与 $x$ 轴、 $y$ 轴交于点 $A$ 、 $B$ ， $M$ 、 $N$ 分别是 $A B$ 、 $O A$ 的中点，点 $P$ 是 $y$ 轴上一个动点，当 $P M + P N$ 的值最小时，点 $P$ 的坐标为．

查看试题解析
13. 在平面直角坐标系中，正方形A₁B₁C₁O、正方形A₂B₂C₂C₁、正方形A₃B₃C₃C₂、正方形A₄B₄C₄C₃、…、正方形A_nB_n∁_nC_n_-₁按如图所示的方式放置，其中点A₁ ， A₂ ， A₃ ， A₄ ， …，A_n均在一次函数y＝kx+b的图象上，点C₁ ， C₂ ， C₃ ， C₄ ， …，∁_n均在x轴上．若点B₁的坐标为（1，1），点B₂的坐标为（3，2），则点A_n的坐标为．

查看试题解析

三、解答题

14. 如图1，在平面直角坐标系中，直线AB交两坐标轴于A、B两点（OA＞OB），且OA、OB的长是一元二次方程x²﹣7x+12＝0的两根．

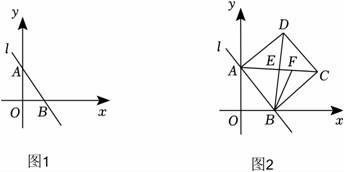(1)、求直线AB的解析式；

(2)、以线段AB为边作正方形ABCD（如图2），对角线AC、BD交于点E，∠CBD的平分线BF交AC于F，求CF的长；

(3)、若M是y轴上任一点，点N是坐标平面内一点，若以A、B、M、N为顶点的四边形是菱形，请直接写出N点的坐标．

查看试题解析
15. 如图1，在平面直角坐标系中， $A$ 点坐标为 $(0 ， 4) ， B$ 点坐标为 $(0 ， - 1) ， C$ 是 $x$ 轴负半轴上一点，且 $A B = A C ， P$ 是 $y$ 轴正半轴上一点，作 $P D ⊥ B C$ 于点 $D$ ，连接OD.

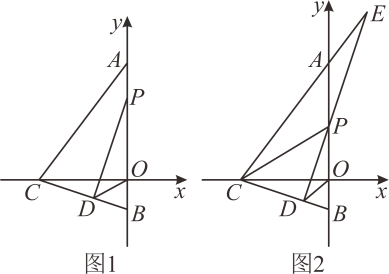(1)、C点坐标为， $B C =$ .

(2)、①当点 $P$ 在线段OA上时，若 $△ O B D$ 是以OB为腰的等腰三角形，请求出所有符合条件的 $P$ 点坐标.
②如图2，设DP交直线AC于点 $E$ ，连结CP，若 $S_{△ A C P} ： S_{△ A E P} = 5 ： 2$ ，则 $S_{△ C O P} =$ (直接写出结果).

查看试题解析

四、综合题

16. 已知直线 $l$ 为 $x + y = 8$ ，点 $P (x ， y)$ 在 $l$ 上，且 $x > 0 ， y > 0$ ，点 $A$ 的坐标为 $(4 ， 0)$ ．

(1)、设 $△ O A P$ 的面积为 $S$ ，求 $S$ 与 $x$ 的函数关系式，并直接写出 $x$ 的取值范围；

(2)、当 $S = 10$ 时，求点 $P$ 的坐标；

(3)、在直线 $l$ 上有一点 $M$ ，使 $O M + M A$ 的和最小，求点 $M$ 的坐标．

查看试题解析
17. 如图，在平面直角坐标系中，直线 $A B$ 与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $B$ ，直线 $O C$ ： $y = - 2 x$ 与直线 $A B$ 交于点 $C$ ，已知 $O A = 2$ ， $O B = 2 O A$ ．

(1)、求直线 $A B$ 的解析式；

(2)、如图 $1$ ，点 $P$ 为直线 $O C$ 上一动点且位于点 $C$ 的左侧， $M$ 、 $Q$ 为 $y$ 轴上两个动点，点 $Q$ 位于点 $M$ 上方，且 $M Q = 2$ ，当 $S_{△ P C B} = 6$ 时，求 $P Q + Q M + M A$ 最小值；

(3)、如图 $2$ ，将 $△ A O B$ 沿着射线 $C O$ 方向平移，平移后 $A$ 、 $O$ 、 $B$ 三点分别对应 $D$ 、 $E$ 、 $F$ 三点，当 $D F$ 过 $O$ 点时停止运动，已知动点 $H$ 在直线 $A B$ 上，在平面直角坐标系中是否存在点 $N$ ，使得以 $H$ 、 $N$ 、 $D$ 、 $F$ 四个点为顶点的四边形为菱形，若存在，请直接写出点 $N$ 的横坐标；若不存在，请说明理由．

查看试题解析