湘教版数学八年级下学期 4.4 用待定系数法确定一次函数表达式同步分层训练基础题
试卷更新日期:2024-03-26 类型:同步测试
一、选择题
-
1. 点在正比例函数的图象上,则的值为( )A、 B、 C、 D、2. 如图,在平面直角坐标系中,、两点在一次函数的图象上,其坐标分别为 , , 下列结论正确的是( )
 A、 , B、 , C、 , D、3. 已知一次函数 图象上的三点 , , ,则 , , 的大小关系是( )A、 B、 C、 D、4. 在平面直角坐标系中,若 , , 则一次函数的图象大致是( )A、
A、 , B、 , C、 , D、3. 已知一次函数 图象上的三点 , , ,则 , , 的大小关系是( )A、 B、 C、 D、4. 在平面直角坐标系中,若 , , 则一次函数的图象大致是( )A、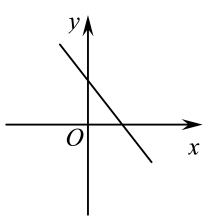 B、
B、 C、
C、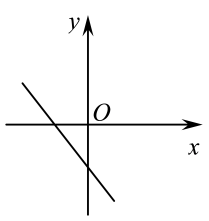 D、
D、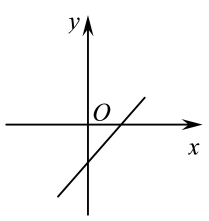 5. 若一次函数 的图像过第一、三、四象限,则函数 ( )A、有最大值 B、有最大值 C、有最小值 D、有最小值6. 一次函数的大致图象是( )A、
5. 若一次函数 的图像过第一、三、四象限,则函数 ( )A、有最大值 B、有最大值 C、有最小值 D、有最小值6. 一次函数的大致图象是( )A、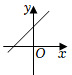 B、
B、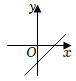 C、
C、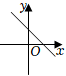 D、
D、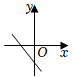 7. 关于函数 , 给出下列说法正确的是:( )
7. 关于函数 , 给出下列说法正确的是:( )①当时,该函数是一次函数;
②若点在该函数图象上,且 , 则;
③若该函数不经过第四象限,则;
④该函数恒过定点 .
A、①②④ B、①③④ C、②③④ D、①②③8. 一次函数 和正比例函数 在同一直角坐标系中的函数图象可能是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 若点 , 都在一次函数的图象上,则 . (填“”或“”)10. 一个水库的水位在最近5h内持续上涨.下表记录了这5h内6个时间点的水位高度,其中x表示时间,y表示水位高度.
x/h
0
1
2
3
4
5
y/m
3
3.3
3.6
3.9
4.2
4.5
根据表格中水位的变化规律,则y与x的函数表达式为.
11. 已知x﹣2y=2,且x>1,y<0,令m=x+2y , 则m的取值范围是 .12. 如图,将八个边长为1的小正方形摆放在平面直角坐标系中.若过原点的直线l将图形分成面积相等的两部分,则直线l的函数表达式为. 13. 已知一次函数(为常数且).(1)、若该一次函数图象经过点 , 则;(2)、当时,函数有最大值11,则的值为 .
13. 已知一次函数(为常数且).(1)、若该一次函数图象经过点 , 则;(2)、当时,函数有最大值11,则的值为 .三、解答题
-
14. 如图,已知直线的图象经过点 , , 且与x轴交于点C .(1)、求直线的解析式;(2)、求的面积.15. 如图,在平面直角坐标系中,直线AB交轴于点(4,0),交轴于点(0,3).
 (1)、求直线的解析式;(2)、是轴上一点,当的面积为5时,求点的坐标.
(1)、求直线的解析式;(2)、是轴上一点,当的面积为5时,求点的坐标.四、综合题