湘教版数学八年级下学期 4.3 一次函数的图像同步分层训练培优题
试卷更新日期:2024-03-26 类型:同步测试
一、选择题
-
1. 把直线y=-5x沿着y轴平移后得到直线AB,直线AB经过点(a,b),且5a+b=-2.则直线AB的函数表达式是( )A、y=-5x+2 B、y=-5x-2 C、y=5x+2 D、y=5x-22. 已知点A(﹣1,m),B(3,n)都在一次函数y=3x+b的图象上,则( )A、m=n B、m>n C、m<n D、m,n的大小关系不确定3. 如图所示,能表示二元一次方程的直线是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,点B、C分别在两条直线和上,点A、D是x轴上两点,若四边形是正方形,则k的值为( )
4. 如图,点B、C分别在两条直线和上,点A、D是x轴上两点,若四边形是正方形,则k的值为( ) A、6 B、5 C、 D、5. 下列各点在一次函数的图象上的是( )A、 B、 C、 D、6. 如图,已知点 , 点M,N分别是直线和直线上的动点,连接 , . 的最小值为( )
A、6 B、5 C、 D、5. 下列各点在一次函数的图象上的是( )A、 B、 C、 D、6. 如图,已知点 , 点M,N分别是直线和直线上的动点,连接 , . 的最小值为( )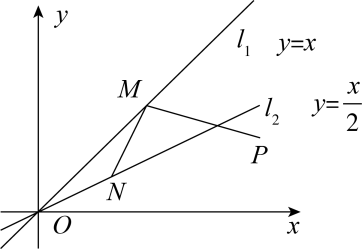 A、2 B、 C、 D、7. 如图,正方形、正方形、正方形的顶点、、和、、、分别在一次函数的图像和轴上,若正比例函数则过点 , 则的值是( )
A、2 B、 C、 D、7. 如图,正方形、正方形、正方形的顶点、、和、、、分别在一次函数的图像和轴上,若正比例函数则过点 , 则的值是( ) A、 B、 C、 D、8. 如图,在平面直角坐标系中,点A1 , A2 , A3 , …,An在x轴上,点B1 , B2 , …,B在直线上,若点A1的坐标为(1,0),且 , , …,都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1 , S2 , …,Sn , 则Sn可表示为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,点A1 , A2 , A3 , …,An在x轴上,点B1 , B2 , …,B在直线上,若点A1的坐标为(1,0),且 , , …,都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1 , S2 , …,Sn , 则Sn可表示为( )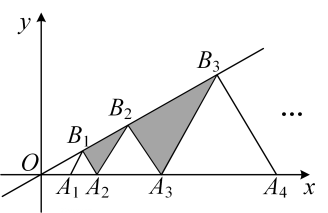 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
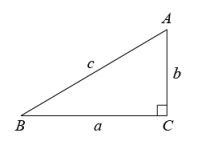
9. 已知一次函数 , 当自变量时,函数y的值是 .10. 已知a , b , c分别是Rt△ABC的三条边长,c为斜边长,∠C=90°,我们把关于x的形如y=的一次函数称为“勾股一次函数”.若点P(-1,)在“勾股一次函数”的图象上,且Rt△ABC的面积是 , 则c的值是 .
 11. 将一次函数的图象先向左平移个单位长度,再向下平移个单位长度后得到的函数解析式为 .12. 如图,直线AB的解析式为y=-x+b , 分别与x轴,y轴交于A , B两点,点A的坐标为(4,0),过点B的直线交x轴负半轴于点C , 且OB:OC=4:1.若在x轴上方存在点D , 使以A , B , D为顶点的三角形与△ABC全等,则点D的坐标为 .
11. 将一次函数的图象先向左平移个单位长度,再向下平移个单位长度后得到的函数解析式为 .12. 如图,直线AB的解析式为y=-x+b , 分别与x轴,y轴交于A , B两点,点A的坐标为(4,0),过点B的直线交x轴负半轴于点C , 且OB:OC=4:1.若在x轴上方存在点D , 使以A , B , D为顶点的三角形与△ABC全等,则点D的坐标为 . 13. 在平面直角坐标系中,横坐标和纵坐标都为整数的点称为整点.已知一次函数 , .(1)、若 , 则、的图象与轴围成的区域内包括边界有个整点;(2)、若、的图象与轴围成的区域内恰有个整点,则的的取值范围是 .
13. 在平面直角坐标系中,横坐标和纵坐标都为整数的点称为整点.已知一次函数 , .(1)、若 , 则、的图象与轴围成的区域内包括边界有个整点;(2)、若、的图象与轴围成的区域内恰有个整点,则的的取值范围是 .三、解答题
-
14. 如图,边长为4的正方形ABCD在平面直角坐标系xOy中,AB⊥y轴,AD⊥x轴,点A在直线y=2x-3上移动.
 (1)、当点A的横坐标为1时,求B,C两点的坐标;(2)、在正方形ABCD移动过程中,直线l始终平分正方形ABCD的面积,求直线l的解析式;(3)、当正方形ABCD有一条边与x轴或y轴重合时,请直接写出所有符合条件的点A的坐标.15. 对于平面直角坐标系中的点 , 给出如下定义:当时,;当时 , k叫做点P的“斜值”.
(1)、当点A的横坐标为1时,求B,C两点的坐标;(2)、在正方形ABCD移动过程中,直线l始终平分正方形ABCD的面积,求直线l的解析式;(3)、当正方形ABCD有一条边与x轴或y轴重合时,请直接写出所有符合条件的点A的坐标.15. 对于平面直角坐标系中的点 , 给出如下定义:当时,;当时 , k叫做点P的“斜值”. (1)、直接写出点的“斜值”k的值;(2)、若点的“斜值” , 且 , 求点P的坐标;(3)、如图,正方形中, , , , 若正方形的边上存在两个点的“斜值”为 , 直接写出m的取值范围.
(1)、直接写出点的“斜值”k的值;(2)、若点的“斜值” , 且 , 求点P的坐标;(3)、如图,正方形中, , , , 若正方形的边上存在两个点的“斜值”为 , 直接写出m的取值范围.四、综合题
-
16. 如图,在平面直角坐标系中,直线与x轴、y轴相交于A、B两点,动点C在线段上,将线段绕着点C顺时针旋转得到 , 此时点D恰好落在直线上时,过点D作轴于点E .
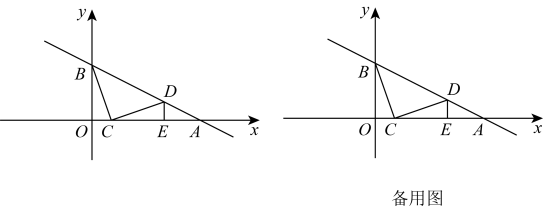 (1)、求证:;(2)、求点D的坐标;(3)、若点P在y轴上,点Q在直线上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标;若不存在,请说明理由.17. 已知:如图,一次函数y= x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
(1)、求证:;(2)、求点D的坐标;(3)、若点P在y轴上,点Q在直线上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标;若不存在,请说明理由.17. 已知:如图,一次函数y= x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E. (1)、直线CD的函数表达式为;(直接写出结果)(2)、点Q为线段DE上的一个动点,连接BQ.
(1)、直线CD的函数表达式为;(直接写出结果)(2)、点Q为线段DE上的一个动点,连接BQ.①若直线BQ将△BDE的面积分为1:2两部分,试求点Q的坐标;
②点Q是否存在某个位置,将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的坐标轴上?若存在,求点Q的坐标;若不存在,请说明理由.