湘教版数学八年级下学期 4.1.2 函数的表示法同步分层训培优题
试卷更新日期:2024-03-26 类型:同步测试
一、选择题
-
1. 某车从甲地到乙地,行驶全程所需的时间与平均速度之间的反比例函数关系如图,当车速为80千米/时,则需要3小时能行驶全程.若该路段行车速度不能超过 , 则行车时间应控制在( )
 A、至多2.4小时 B、小于2.4小时 C、至少2.4小时 D、大于2.4小时2. 如图①,在矩形中,动点从出发,以恒定的速度,沿方向运动到点处停止.设点运动的路程为 . 面积为 , 若与的函数图象如图②所示,则矩形的面积为( )
A、至多2.4小时 B、小于2.4小时 C、至少2.4小时 D、大于2.4小时2. 如图①,在矩形中,动点从出发,以恒定的速度,沿方向运动到点处停止.设点运动的路程为 . 面积为 , 若与的函数图象如图②所示,则矩形的面积为( ) A、36 B、54 C、72 D、813. 如图①,公路上有三家商店,甲、乙两人分别从两家商店同时沿公路按如图所示的方向向右匀速步行.设出发后,甲距离商店为 , 乙距离商店为 . 当时,已知关于的函数图象在同一平面直角坐标系中如图②所示,根据图中所给信息下列描述正确的是( )
A、36 B、54 C、72 D、813. 如图①,公路上有三家商店,甲、乙两人分别从两家商店同时沿公路按如图所示的方向向右匀速步行.设出发后,甲距离商店为 , 乙距离商店为 . 当时,已知关于的函数图象在同一平面直角坐标系中如图②所示,根据图中所给信息下列描述正确的是( ) A、乙的速度为 B、两商店相距 C、当甲到达商店时,甲、乙两人相距1650m D、当时,甲、乙两人相距1500m4. 甲、乙、丙、丁四个人步行的路程和所用的时间如图所示,按平均速度计算.走得最快的是( )
A、乙的速度为 B、两商店相距 C、当甲到达商店时,甲、乙两人相距1650m D、当时,甲、乙两人相距1500m4. 甲、乙、丙、丁四个人步行的路程和所用的时间如图所示,按平均速度计算.走得最快的是( )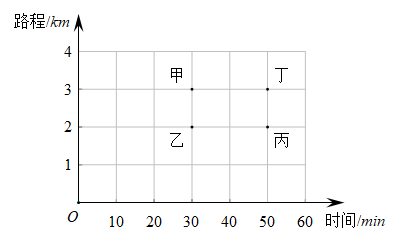 A、甲 B、乙 C、丙 D、丁5. 小强所在学校离家距离为2千米,某天他放学后骑自行车回家,先骑了5分钟后,因故停留10分钟,再继续骑了5分钟到家,下面哪一个图象能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的关系( )A、
A、甲 B、乙 C、丙 D、丁5. 小强所在学校离家距离为2千米,某天他放学后骑自行车回家,先骑了5分钟后,因故停留10分钟,再继续骑了5分钟到家,下面哪一个图象能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的关系( )A、 B、
B、 C、
C、 D、
D、 6. 2023年10月22日,2023云丘山越野赛完美收官。在越野赛中,甲、乙两选手的行程y(km)随时间x(h)变化的图象(全程)如图所示.给出下列四种说法:①起跑后1h内,甲在乙的前面;②第1h两人都跑了10km;③甲比乙先到达终点;④两人都跑了20km.其中正确的是( )
6. 2023年10月22日,2023云丘山越野赛完美收官。在越野赛中,甲、乙两选手的行程y(km)随时间x(h)变化的图象(全程)如图所示.给出下列四种说法:①起跑后1h内,甲在乙的前面;②第1h两人都跑了10km;③甲比乙先到达终点;④两人都跑了20km.其中正确的是( ) A、① B、①② C、①②④ D、②③④7. 学校的自动饮水机,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降.此时水温(℃)与通电时间成反比例关系.当水温降至20℃时,饮水机再自动加热,若水温在20℃时接通电源,水温y与通电时间x之间的关系如图所示,则下列说法中正确的是( )
A、① B、①② C、①②④ D、②③④7. 学校的自动饮水机,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降.此时水温(℃)与通电时间成反比例关系.当水温降至20℃时,饮水机再自动加热,若水温在20℃时接通电源,水温y与通电时间x之间的关系如图所示,则下列说法中正确的是( ) A、水温从20℃加热到100℃,需要 B、水温下降过程中,y与x的函数关系式是 C、上午8点接通电源,可以保证当天9:30能喝到不超过40℃的水 D、水温不低于30℃的时间为8. 如图,扇形的半径 , 圆心角 , 是上不同于 , 的动点,过点作于点 , 作于点 , 连接 , 点在线段上,且 . 设的长为 , 的面积为 , 下面表示与的函数关系式的图象可能是( )
A、水温从20℃加热到100℃,需要 B、水温下降过程中,y与x的函数关系式是 C、上午8点接通电源,可以保证当天9:30能喝到不超过40℃的水 D、水温不低于30℃的时间为8. 如图,扇形的半径 , 圆心角 , 是上不同于 , 的动点,过点作于点 , 作于点 , 连接 , 点在线段上,且 . 设的长为 , 的面积为 , 下面表示与的函数关系式的图象可能是( )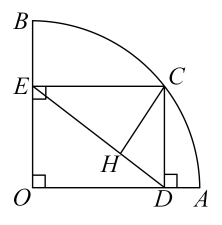 A、
A、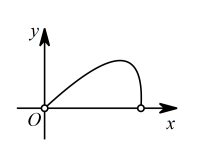 B、
B、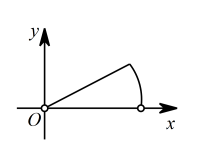 C、
C、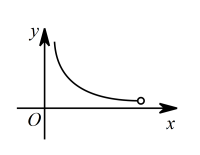 D、
D、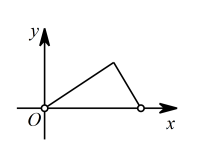
二、填空题
-
9. 已知 , 若 , 则 .10. 观察下列图形及表格:
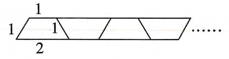
梯形个数
1
2
3
4
5
6
周长
5
8
11
14
17
20
则周长与梯形个数之间的关系式为.
11. 甲、乙两种物质的溶解度与温度之间的对应关系如图所示,下列说法中,
甲、乙两种物质的溶解度均随着温度的升高而增大;
当温度升高至时,甲的溶解度比乙的溶解度小;
当温度为时,甲、乙的溶解度都小于;
当温度为时,甲、乙的溶解度相同.
所有正确结论的序号是 .12. 在中,∠C=90°,AC=6,BC=8,设P是BC上任一点,P点与B、C不重合,且 , 若 , 则与之间的函数关系式是 , 自变量取值范围为 .13. 如图①,底面积为的空圆柱容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器内匀速注水,注满为止,在注水过程中,水面高度与注水时间之间的关系如图②,若“几何体”的下方圆柱的底面积为 , 则图②中的的值为 , “几何体”上方圆柱体的厎面积为 .

三、解答题
-
14. 如图1,甲、乙两人在跑道上进行折返跑,和是相邻的两条赛道(看成两条互相平行的线段),甲在赛道上以的速度从出发,到达后,以同样的速度返回 , 然后重复上述过程;乙在赛道上从出发,到达后以相同的速度回到 , 然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,乙到边的距离为与运动时间的函数图象如图2所示.
 (1)、赛道的长度是 , 乙的速度是;当时,甲、乙两人第一次相遇;(2)、当 ▲ 时,甲、乙两人第二次相遇?并求此时距离边多远?15. 甲和乙两人同时开车从A地出发,沿一条笔直的公路匀速前往相距450千米的B地,已知甲的速度大于乙的速度,1小时后,甲发现有物品落在A地,于是立即按原速度返回A地取物品,返回途中与乙相遇,在第2小时时取到物品后立即提速20%继续前往B地(所有掉头时间和取物品的时间忽略不计),在第5小时时再次遇到乙,并超过乙.已知甲和乙之间的距离y(千米)与甲车行驶的时间x(小时)之间的部分关系如图所示.根据图象解答下列问题.
(1)、赛道的长度是 , 乙的速度是;当时,甲、乙两人第一次相遇;(2)、当 ▲ 时,甲、乙两人第二次相遇?并求此时距离边多远?15. 甲和乙两人同时开车从A地出发,沿一条笔直的公路匀速前往相距450千米的B地,已知甲的速度大于乙的速度,1小时后,甲发现有物品落在A地,于是立即按原速度返回A地取物品,返回途中与乙相遇,在第2小时时取到物品后立即提速20%继续前往B地(所有掉头时间和取物品的时间忽略不计),在第5小时时再次遇到乙,并超过乙.已知甲和乙之间的距离y(千米)与甲车行驶的时间x(小时)之间的部分关系如图所示.根据图象解答下列问题. (1)、乙的速度为 千米/小时;(2)、甲提速后的速度为多少千米/小时;(3)、当甲到达B地时,乙离B地的距离为多少千米.
(1)、乙的速度为 千米/小时;(2)、甲提速后的速度为多少千米/小时;(3)、当甲到达B地时,乙离B地的距离为多少千米.四、综合题
-
16. 如图,甲、乙两人分别骑自行车和摩托车沿相同路线由A地到B地,行驶过程中的时间与路程图象如图所示,请根据图象回答下列问题:
 (1)、先出发,提前小时;(2)、运动过程中甲的速度为:千米/小时,乙的速度为:千米/小时;(3)、请直接写出在甲的行进过程中,当甲、乙两人相距15千米时,自变量x的值是多少?17. 小明家、新华书店、学校在一条笔直的公路旁,某天小明骑车上学,当他骑了一段后,想起要买某本书,于是又返回到刚经过的新华书店,买到书后继续骑车去学校,他本次骑车上学的过程中离家距离与所用的时间的关系如图所示,请根据图象提供的信息回答下列问题:
(1)、先出发,提前小时;(2)、运动过程中甲的速度为:千米/小时,乙的速度为:千米/小时;(3)、请直接写出在甲的行进过程中,当甲、乙两人相距15千米时,自变量x的值是多少?17. 小明家、新华书店、学校在一条笔直的公路旁,某天小明骑车上学,当他骑了一段后,想起要买某本书,于是又返回到刚经过的新华书店,买到书后继续骑车去学校,他本次骑车上学的过程中离家距离与所用的时间的关系如图所示,请根据图象提供的信息回答下列问题: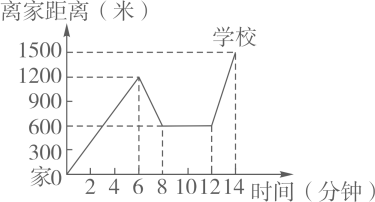 (1)、小明家到学校的距离是米;小明在书店停留了分钟;(2)、如果骑车的速度超过了300米/分就超越了安全限度,小明买到书后继续骑车到学校的这段时间的骑车速度在安全限度内吗?请说明理由;(3)、请直接写出小明出发后多长时间离家的距离为900米?
(1)、小明家到学校的距离是米;小明在书店停留了分钟;(2)、如果骑车的速度超过了300米/分就超越了安全限度,小明买到书后继续骑车到学校的这段时间的骑车速度在安全限度内吗?请说明理由;(3)、请直接写出小明出发后多长时间离家的距离为900米?