湘教版数学八年级下学期 4.1.2 函数的表示法同步分层训练提升题
试卷更新日期:2024-03-26 类型:同步测试
一、选择题
-
1. 两个变量y与x之间的关系如图所示,那么y随x的增大而( )
 A、增大 B、减小 C、不变 D、有时增大有时减小2. 下列图象中,y不是x的函数图象的是( )A、
A、增大 B、减小 C、不变 D、有时增大有时减小2. 下列图象中,y不是x的函数图象的是( )A、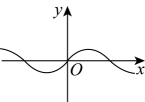 B、
B、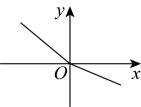 C、
C、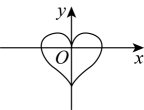 D、
D、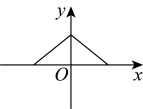 3. 如图是底部放有一个实心铁球的长方体水槽轴截面示意图,现向水槽匀速注水,下列图象中能大致反映水槽中水的深度(y)与注水时间(x)关系的是( )
3. 如图是底部放有一个实心铁球的长方体水槽轴截面示意图,现向水槽匀速注水,下列图象中能大致反映水槽中水的深度(y)与注水时间(x)关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 甲、乙两车从地出发,匀速驶往地.乙车出发h后,甲车才沿相同的路线开始行驶.甲车先到达地并停留分钟后,又以原速按原路线返回,直至与乙车相遇.图中的折线段表示从开始到相遇止,两车之间的距离与甲车行驶的时间x(h)的函数关系的图象,则( )
4. 甲、乙两车从地出发,匀速驶往地.乙车出发h后,甲车才沿相同的路线开始行驶.甲车先到达地并停留分钟后,又以原速按原路线返回,直至与乙车相遇.图中的折线段表示从开始到相遇止,两车之间的距离与甲车行驶的时间x(h)的函数关系的图象,则( ) A、甲车的速度是 B、 , 两地的距离是 C、乙车出发4.5h时甲车到达地 D、甲车出发4.5h最终与乙车相遇5. 在年的卡塔尔世界杯中,阿根廷守门员马丁内斯表现突出,他大脚开出去的球的高度与球在空中运行时间的关系,用图象描述大致是如图中的( )A、
A、甲车的速度是 B、 , 两地的距离是 C、乙车出发4.5h时甲车到达地 D、甲车出发4.5h最终与乙车相遇5. 在年的卡塔尔世界杯中,阿根廷守门员马丁内斯表现突出,他大脚开出去的球的高度与球在空中运行时间的关系,用图象描述大致是如图中的( )A、 B、
B、 C、
C、 D、
D、 6. 如图是一种轨道示意图,其中和均为半圆,点M,A,C,N依次在同一直线上,且 . 现有两个机器人(看成点)分别从M,N两点同时出发,沿着轨道以大小相同的速度匀速移动,其路线分别为和 . 若移动时间为x,两个机器人之间距离为y,则y与x关系的图象大致是( )
6. 如图是一种轨道示意图,其中和均为半圆,点M,A,C,N依次在同一直线上,且 . 现有两个机器人(看成点)分别从M,N两点同时出发,沿着轨道以大小相同的速度匀速移动,其路线分别为和 . 若移动时间为x,两个机器人之间距离为y,则y与x关系的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 甲、乙两车从A地出发,沿同一路线驶向B地. 甲车先出发匀速驶向B地,40 min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时. 由于满载货物,为了行驶安全,速度减少了50 km/h,结果与甲车同时到达B地. 甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:①a=4.5;②甲的速度是60 km/h;③乙出发80 min追上甲;④乙刚到达货站时,甲距B地180 km.其中正确的有( )
7. 甲、乙两车从A地出发,沿同一路线驶向B地. 甲车先出发匀速驶向B地,40 min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时. 由于满载货物,为了行驶安全,速度减少了50 km/h,结果与甲车同时到达B地. 甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:①a=4.5;②甲的速度是60 km/h;③乙出发80 min追上甲;④乙刚到达货站时,甲距B地180 km.其中正确的有( ) A、1个 B、2个 C、3个 D、4个8. 是一种新型的半导体陶瓷材料,它有一个根据需要设定的温度,称为“居里点温度”,低于这个温度时,其电阻值随温度的升高而减小,高于这个温度时,电阻值则随温度的升高而增大.用材料制成的电热器具有发热、控温双重功能,应用十分广泛.如图1是某款家用电灭蚊器,它的发热部分就使用了发热材料,其电阻值随温度变化的关系图像如图2所示,发热部分的电功率P与电阻R和电压U的关系见图3.下列说法不正确的是( ).
A、1个 B、2个 C、3个 D、4个8. 是一种新型的半导体陶瓷材料,它有一个根据需要设定的温度,称为“居里点温度”,低于这个温度时,其电阻值随温度的升高而减小,高于这个温度时,电阻值则随温度的升高而增大.用材料制成的电热器具有发热、控温双重功能,应用十分广泛.如图1是某款家用电灭蚊器,它的发热部分就使用了发热材料,其电阻值随温度变化的关系图像如图2所示,发热部分的电功率P与电阻R和电压U的关系见图3.下列说法不正确的是( ). A、由图2,可知该发热材料的“居里点温度”是 B、当时,该发热材料的电阻值为 C、若电压保持不变,当时,发热部分的电功率最大 D、若电压保持不变,发热部分的电功率随温度的升高而增大
A、由图2,可知该发热材料的“居里点温度”是 B、当时,该发热材料的电阻值为 C、若电压保持不变,当时,发热部分的电功率最大 D、若电压保持不变,发热部分的电功率随温度的升高而增大二、填空题
-
9. 周末,自行车骑行爱好者甲、乙两人相约沿同一路线从A地出发前往B地进行骑行训练,甲、乙分别以不同的速度匀速骑行,乙比甲早出发5分钟.乙骑行25分钟后,甲以原速的继续骑行,经过一段时间,甲先到达B地,乙一直保持原速前往B地.在此过程中,甲、乙两人相距的路程y(米)与乙骑行的时间x(分钟)之间的关系如图所示,则乙比甲晚分钟到达B地.
 10. 某公司新产品上市30天全部售完,图1表示产品的市场日销售量与上市时间之间的关系,图2表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是元.
10. 某公司新产品上市30天全部售完,图1表示产品的市场日销售量与上市时间之间的关系,图2表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是元. 11. A、B两地相距630千米客车、货车分别从A、B两地同时出发,匀速相向行驶货车两小时可到达途中C站,客车需9小时到达C站.货车的速度是客车的 ,客、货车到C站的距离分别为 、 (千米),它们与行驶时间x(小时)之间的函数关系如图.下列说法:①客、货两车的速度分别为60千米小时,45千米/小时;②P点横坐标为12;③A、C两站间的距离是540千米;④E点坐标为(6,180),其中正确的说法是(填序号).
11. A、B两地相距630千米客车、货车分别从A、B两地同时出发,匀速相向行驶货车两小时可到达途中C站,客车需9小时到达C站.货车的速度是客车的 ,客、货车到C站的距离分别为 、 (千米),它们与行驶时间x(小时)之间的函数关系如图.下列说法:①客、货两车的速度分别为60千米小时,45千米/小时;②P点横坐标为12;③A、C两站间的距离是540千米;④E点坐标为(6,180),其中正确的说法是(填序号).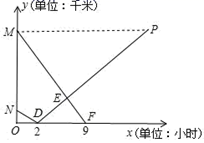 12. 如图1,在中,动点从点出发沿折线匀速运动至点后停止.已知点的运动速度是每秒2个单位长度,设点运动时间为 , 线段的长度为 , 图2是与的函数关系的大致图象,其中点为曲线的最低点,则的高长是.
12. 如图1,在中,动点从点出发沿折线匀速运动至点后停止.已知点的运动速度是每秒2个单位长度,设点运动时间为 , 线段的长度为 , 图2是与的函数关系的大致图象,其中点为曲线的最低点,则的高长是. 13. 为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
13. 为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:汽车行驶时间(小时)
0
1
2
3
油箱剩余油量(升)
50
42
34
26
(1)、上表反映的是哪两个变量之间的关系.(2)、根据上表可知,汽车行数4小时时,该车油箱的剩余油量为升,汽车每小时耗油升.(3)、请直接写出两个变量之间的关系式.三、解答题
-
14. 已知y与x-1成反比例,且当x=-5时,y=2.(1)、求y与x的函数关系式;(2)、当x=5时,求y的值.15. 有这样一个问题:探究函数的图象与性质.
小明根据学习函数的经验,对函数的图象与性质进行了探究.
(1)、函数的自变量的取值范围是;(2)、下表是与的几组对应值,请你求的值;(3)、如图,在平面直角坐标系中,描出了以上表中各组数值所对应的点,请你画出该函数的图象; (4)、结合函数的图象,写出该函数的一条性质: .
(4)、结合函数的图象,写出该函数的一条性质: .四、综合题
-
16. 某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示.根据图象解答下列问题:
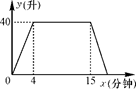 (1)、洗衣机的进水时间是多少分钟?清洗时洗衣机中水量为多少升?(2)、已知洗衣机的排水速度为每分钟19升.
(1)、洗衣机的进水时间是多少分钟?清洗时洗衣机中水量为多少升?(2)、已知洗衣机的排水速度为每分钟19升.①求排水时洗衣机中的水量y(升)与时间x(分钟)与之间的关系式;
②如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量.
17. 甲、乙两车早上从A城车站出发匀速前往B城车站,在整个行程中,两车离开A城的距离s与时间t的对应关系如图所示. (1)、A,B两城之间距离是多少?(2)、求甲、乙两车的速度分别是多少?(3)、乙车出发多长时间追上甲车?(4)、从乙车出发后到甲车到达B城车站这一时间段,在何时间点两车相距40km?
(1)、A,B两城之间距离是多少?(2)、求甲、乙两车的速度分别是多少?(3)、乙车出发多长时间追上甲车?(4)、从乙车出发后到甲车到达B城车站这一时间段,在何时间点两车相距40km?