2023-2024学年湘教版初中数学八年级下学期 4.1.2 函数的表示法同步分层训练基础题
试卷更新日期：2024-03-26 类型：同步测试
一、选择题
-
1. 如图曲线中不能表示是的函数的是（ ）A、
B、
C、
D、
2. 下列不能表示是的函数的是（ ）A、
B、x 0 5 10 15 y 3 3.5 4 4.5 
C、
D、
3. 如图所示图象中，表示y是x的函数的有（ ）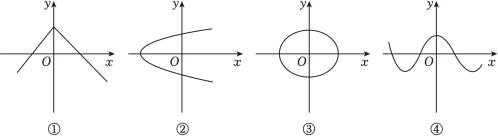
A、①②③④ B、①②③ C、①④ D、②③4. 已知电压U、电流I、电阻R三者之间的关系式为U=IR，实际生活中，由于给定的已知量不同，因此会有不同的图象，但图象不可能是（ ）A、
B、
C、
D、
5. 小聪某次从家出发去公园游玩的行程如图所示，他离家的路程为s米，所经过的时间为t分钟.下列图象中，能近似刻画s与t之间关系的是（ ）
A、
B、
C、
D、
6. 龟兔赛跑之后，输了比赛的兔子决定和乌龟再赛一场.如图的函数图象表示了龟兔再次赛跑的过程(x表示兔子和乌龟从起点出发所走的时间，y₁，y₂分别表示兔子和乌龟所走的路程).下列说法错误的是（ ）
A、兔子和乌龟比赛的路程是500米 B、中途，兔子比乌龟多休息了35分钟 C、兔子比乌龟多走了50米 D、比赛结果，兔子比乌龟早5分钟到达终点7. 如图1，小亮家、报亭、羽毛球馆在一条直线上.小亮从家跑步到羽毛球馆打羽毛球，再去报亭看报，最后散步回家.小亮离家距离y与时间x之间的关系如图2所示.下列结论错误的是（ ）
A、小亮从家到羽毛球馆用了7分钟 B、小亮从羽毛球馆到报亭平均每分钟走75米 C、报亭到小亮家的距离是400米 D、小亮打羽毛球的时间是37分钟二、填空题
-
8. 如图，某植物天后的高度为 ， 反映了与之间的关系，则该植物平均每天长高cm.
9. 如图是在固定的电压下，一电阻的阻值与通过该电阻的电流之间的函数关系图.根据图象，当自变量时，函数值为.
10. 由于持续高温和连日无雨，某水库的蓄水量随着时间的增加而减少．水库的蓄水量V（万立方米）与干旱持续时间t（天）之间的函数关系如图所示．
根据图象回答下列问题：
(1)、干旱持续10天时，蓄水量为万立方米．(2)、如果蓄水量小于400万立方米时，将发出严重干旱警报，那么干旱天后将发出严重干旱警报．11. 小华和小兰两家相距2400米，他们相约到两家之间的剧院看戏，两人同时从家出发匀速前行，出发15分钟后，小华发现忘带门票，立即以原来速度的1.5倍返回家中，取完东西后仍以返回时的速度去见小兰；而小兰在出发30分钟时到达剧院，等待10分钟后未见小华，于是仍以原来的速度，从剧院出发前往小华家，途中两人相遇．假设小华掉头、取票时间均忽略不计．两人之间的距离y（米）与小华出发时间x（分钟）之间的关系如图所示，则当两人相遇时，小兰距离剧院有 米．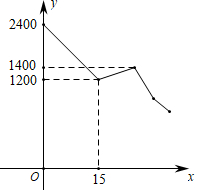
12. 如图1，小亮家、报亭、羽毛球馆在一条直线上.小亮从家跑步到羽毛球馆打羽毛球，再去报亭看报，最后散步回家.小亮离家距离y与时间x之间的关系如图2所示.下列结论正确的是(填序号).
①小亮从家到羽毛球馆用了7分钟.
②小亮从羽毛球馆到报亭平均每分钟走75米.
③报亭到小亮家的距离是400米.
④小亮打羽毛球的时间是37分钟。
三、解答题
-
13. 小红和小玉是同班同学，也是邻居，某天早晨，小红7：10先出发去学校，走了一段后，在途中停下吃早餐，后来发现上学时间快到了，就跑步到学校；小玉骑自行车沿相同路线到学校.如图是她们从家到学校已走的路程s（m）和所用时间t（min）的关系图.
请根据图象回答下列问题：
(1)、 小红到学校的路程是m，小红吃早餐用了min；(2)、 小玉骑自行车的速度为m/min；(3)、 小红从家到学校的平均速度为m/min；(4)、 小玉骑自行车出发几分钟后追上小红？14. 甘肃地震牵动全国，甲、乙两人沿同一条路用货车从地匀速开往相距的灾区地运送救灾物资.如图，和分别表示甲、乙与地的距离与行驶的时间之间的关系．
(1)、甲出发后，两人相遇，这时他们与地的距离为；(2)、甲的速度是 ， 乙的速度是；(3)、乙从地出发时到达地．四、综合题
-
15. 6月13日，某港口的潮水高度y（）和时间x（h）的部分数据及函数图象如下：(数据来自某海洋研究所)
(1)、数学活动：①根据表中数据，通过描点、连线（光滑曲线）的方式补全该函数的图象．
②观察函数图象，当时，y的值为多少？当y的值最大时，x的值为多少？ ▲ ， ▲ .
(2)、数学思考：结合函数图象，写出该函数的两条性质或结论 ．
x(h)
…
11
12
13
14
15
16
17
18
…
y(cm)
…
189
137
103
80
101
133
202
260
…
(3)、数学应用：当潮水高度超过260 ， 货轮能安全进出港口．问当天货轮进出港口最佳时间段？
16. 德国心理学家艾宾浩斯研究发现，遗忘在新事物学习之后立即开始，而且遗忘的进程并不是均匀的．如果把学习后的时间记为x（时），记忆留存率记为y（%），则根据实验数据可绘制出曲线（如图所示），即著名的“艾宾浩斯遗忘曲线”．该曲线对人类记忆认知研究产生了重大影响．
(1)、y是关于x的函数吗？为什么？(2)、请说明点D的实际意义．(3)、根据图中信息，对新事物学习提出一条合理的建议．