湘教版数学八年级下学期 4.1.1 变量与函数同步分层训练培优题
试卷更新日期:2024-03-26 类型:同步测试
一、选择题
-
1. 函数的自变量的取值范围是( )A、 B、 C、且 D、2. 下列关系式中,y不是x的函数的是( )A、 B、y=2x2 C、y2=x D、y=(x≥0)3. 若点是抛物线上的两点,则、的大小关系是( )A、 B、 C、 D、4. 如图所示的图象分别给出了x与y的对应关系,其中表示y是x的函数的是( ).A、
 B、
B、 C、
C、 D、
D、 5. 下列各曲线中不能表示y是x的函数的是( )A、
5. 下列各曲线中不能表示y是x的函数的是( )A、 B、
B、 C、
C、 D、
D、 6. 下列图象,不能表示是的函数的是( )A、
6. 下列图象,不能表示是的函数的是( )A、 B、
B、 C、
C、 D、
D、 7. 函数y=的自变量x的取值范围是( )A、x>1 B、x>1且x≠3 C、x≥1 D、x≥1且x≠38. 已知: 表示不超过x的最大整数.例: .令关于 的函数 ( 是正整数),例: .则下列结论错误的是( )A、 B、 C、 D、 或1
7. 函数y=的自变量x的取值范围是( )A、x>1 B、x>1且x≠3 C、x≥1 D、x≥1且x≠38. 已知: 表示不超过x的最大整数.例: .令关于 的函数 ( 是正整数),例: .则下列结论错误的是( )A、 B、 C、 D、 或1二、填空题
-
9. 函数y=的自变量x的取值范围为 .10. 三角形的面积公式中S=ah其中底边a保持不变,则常量是 ,变量是 .11. 小邢到单位附近的加油站加油,下图所示是他所用的加油机上的数据显示牌,则数据中的变量是
 12. 函数y=--的最大值为.13. 对于正数 ,规定 ,例如: , , , ……利用以上规律计算:
12. 函数y=--的最大值为.13. 对于正数 ,规定 ,例如: , , , ……利用以上规律计算:的值为:.
三、解答题
-
14. 随着日期的变化,国外新冠肺炎疫情形势依然严峻,结合如图的两条曲线,你能判断累计确诊人数是日期的函数吗?现有确诊人数是日期的函数吗?
 15. 在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°.矩形CODE的顶点D , E , C分别在OA , AB , OB上,OD=2.
15. 在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°.矩形CODE的顶点D , E , C分别在OA , AB , OB上,OD=2.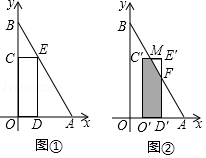
(Ⅰ)如图①,求点E的坐标;
(Ⅱ)将矩形CODE沿x轴向右平移,得到矩形C′O′D′E′,点C , O , D , E的对应点分别为C′,O′,D′,E′.设OO′=t , 矩形C′O′D′E′与△ABO重叠部分的面积为S .
①如图②,当矩形C′O′D′E′与△ABO重叠部分为五边形时,C′E′,E′D′分别与AB相交于点M , F , 试用含有t的式子表示S , 并直接写出t的取值范围;
②当 ≤S≤5 时,求t的取值范围(直接写出结果即可).
四、综合题



