湘教版数学八年级下学期 3.3 轴对称和平移的坐标表示同步分层训练培优题

试卷更新日期：2024-03-26 类型：同步测试

进入出卷网下载

一、选择题

1. A（-3，2）关于原点的对称点是B，B关于x轴的对称点是C，则点C的坐标是（　）

A、（3，2） B、（-3，2） C、（3，-2） D、（-2，3）

查看试题解析
2. 若点 $A (x + y ， 1)$ 与点 $B (- 3 ， x - y)$ 关于x轴对称，则（）

A、 $x = - 2$ ， $y = 1$ B、 $x = - 2$ ， $y = - 1$ C、 $x = 2$ ， $y = - 1$ D、 $x = 2$ ， $y = 1$

查看试题解析
3. 已知点P（m﹣1，4）与点Q（2，n﹣2）关于x轴对称，则mⁿ的值为（　　）

A、9 B、﹣9 C、 $- \frac{1}{9}$ D、 $\frac{1}{9}$

查看试题解析
4. 点 $P (2 ， - 3)$ 关于原点对称的点 $P^{'}$ 的坐标是（）

A、 $(2 ， 3)$ B、 $(- 2 ， - 3)$ C、 $(- 3 ， 2)$ D、 $(- 2 ， 3)$

查看试题解析
5. 若点 $A (x + y ， 1)$ 与 $B (- 3 ， x - y)$ 关于 $x$ 轴对称，则（）

A、 $x = - 2$ ， $y = 1$ B、 $x = - 2$ ， $y = - 1$ C、 $x = 2$ ， $y = - 1$ D、 $x = 2$ ， $y = 1$

查看试题解析
6. 如图，在△OAB中，顶点O（0，0），A（﹣2，3），B（2，3），将△OAB与正方形ABCD组成的图形绕点O顺时针旋转，每次旋转90°，则第2023次旋转结束时，点D的坐标为（　　）

A、（﹣2，7） B、（7，2） C、（2，﹣7） D、（﹣7，﹣2）

查看试题解析
7. 如图，在平面直角坐标系中，Rt△AOB的一条直角边OB在x轴上，点A的坐标为（-6，4）；Rt△COD中，∠COD＝90°，OD＝4 $\sqrt{3}$ ， ∠D＝30°，连接BC，点M是BC中点，连接AM．将Rt△COD以点O为旋转中心按顺时针方向旋转，在旋转过程中，线段AM的最小值是（）

A、3 B、6 $\sqrt{2}$ -4 C、2 $\sqrt{13}$ -2 D、2

查看试题解析
8. 如图所示，矩形ABOC的顶点O（0，0），A（－2 $\sqrt{3}$ ， 2），对角线交点为P，若矩形绕点O逆时针旋转，每次旋转90°，则第74次旋转后点P的落点坐标为（）

A、(1， $\sqrt{3}$ ) B、（2，0） C、(1，- $\sqrt{3}$ ) D、( $\sqrt{3}$ ， -1)

查看试题解析

二、填空题

9. 点 $M (2 ， - 3)$ 向左平移5个单位长度，再向上平移6个单位长度对应点 $M^{'}$ 的坐标为．

查看试题解析
10. 在平面直角坐标系中，已知点A(m，2)与点B(3，n).若点A和点B关于x轴对称，则m= ， n=；若点A和点B关于y轴对称，则m= ， n=；若点A和点B关于原点对称，则m= ， n.

查看试题解析
11. 点E(a，－5)与点F(－2，b)关于y轴对称，则a＝， b＝.

查看试题解析
12. 如图所示，在直角坐标系中，等腰直角 $△ A B O$ 的顶点 $O$ 是坐标原点，点 $A$ 的坐标是 $(- 6 ， 0)$ ，直角顶点 $B$ 在第二象限，把 $△ A B O$ 绕点 $O$ 旋转15°到 $△ A_{1} B_{1} O$ ，点 $A$ 与 $A_{1}$ 对应，点 $B$ 与点 $B_{1}$ 对应，那么点 $B_{1}$ 的坐标是．

查看试题解析
13. 如图，在平面直角坐标系中，点 $A (- 1 ， 0)$ ，点 $A$ 第 $1$ 次向上跳动 $1$ 个单位至点 $A_{1} (- 1 ， 1)$ ，紧接着第 $2$ 次向右跳动 $2$ 个单位至点 $A_{2} (1 ， 1)$ ，第 $3$ 次向上跳动 $1$ 个单位，第 $4$ 次向左跳动 $3$ 个单位，第 $5$ 次又向上跳动 $1$ 个单位，第 $6$ 次向右跳动 $4$ 个单位， $\dots$ 依此规律跳动下去，点 $A$ 第 $2023$ 次跳动至点 $A_{2023}$ 的坐标是．

查看试题解析

三、解答题

14. 已知点P(-1，2)，点P关于x轴的对称点为P，关于直线y=-1的对称点为P₂ ，关于直线y=3的对称点为P₃ ，分别写出P₁ ， P₂ ， P₃的坐标，想一想，试写出点Q(x，y)关于直线y=a对称点的坐标．

查看试题解析
15. 对于正数 $x$ ，用符号 $[x]$ 表示 $x$ 的整数部分，例如 $[0.1] = 0$ ， $[2.5] = 2$ ， $[3] = 3 .$ 点 $A (a ， b)$ 在第一象限内，以 $A$ 为对角线的交点画一个矩形，使它的边分别与两坐标轴垂直 $.$ 其中垂直于 $y$ 轴的边长为 $a$ ，垂直于 $x$ 轴的边长为 $[b] + 1$ ，那么，把这个矩形覆盖的区域叫做点 $A$ 的矩形域 $.$ 例如：点 $(3 ， \frac{3}{2})$ 的矩形域是一个以 $(3 ， \frac{3}{2})$ 为对角线交点，长为 $3$ ，宽为 $2$ 的矩形所覆盖的区域，如图 $1$ 所示，它的面积是 $6$ ．
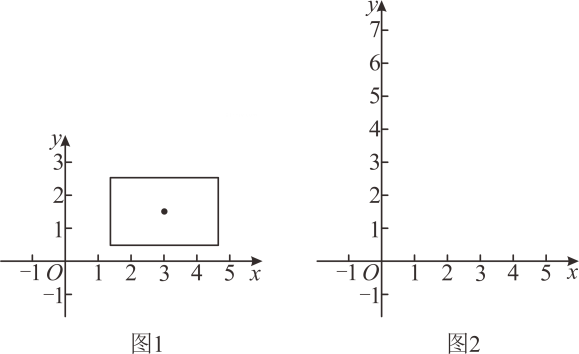
根据上面的定义，回答下列问题：

(1)、在图 $2$ 所示的坐标系中画出点 $(2 ， \frac{7}{2})$ 的矩形域，该矩形域的面积是；

(2)、点 $P (2 ， \frac{7}{2})$ ， $Q (a ， \frac{7}{2}) (a > 0)$ 的矩形域重叠部分面积为 $1$ ，则 $a$ 的值为．

查看试题解析

四、综合题

16. 如图所示，点 $A$ 的坐标为 $(1 ， 0)$ ，点 $B$ 的坐标为 $(0 ， 2)$ ，将三角形 $O A B$ 沿 $x$ 轴负方向平移3个单位长度，平移后的图形为三角形 $D E C$ ．

(1)、直接写出点 $C$ 的坐标；

(2)、在四边形 $A B C D$ 中，点 $P$ 从点 $B$ 出发沿 $B C - C D$ 移动，若点 $P$ 的速度为每秒1个单位长度，运动时间为 $t$ 秒，回答下列问题：
① $t =$ ▲ 秒时，点 $P$ 的横坐标与纵坐标互为相反数；

②用含有 $t$ 的式子表示点 $P$ 的坐标；

③当 $3 < t < 5$ 时，设 $∠ C B P = x °$ ； $∠ P A D = y °$ ， $∠ B P A = z °$ ，探索 $x$ ， $y$ ， $z$ 之间的数量关系，并说明理由．

查看试题解析
17. 在直角坐标平面内，已知点A的坐标为 $(3 ， 1)$ ，点B与点A关于原点对称，点C的坐标为 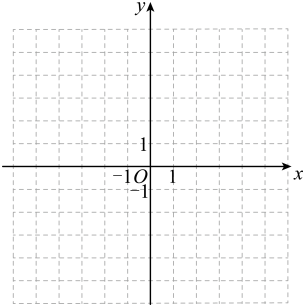$(1 ， - 1)$ ．

(1)、画出 $△ A B C$ ：

(2)、写出点B的坐标和 $△ A B C$ 的面积：B ， $S_{△ A B C} =$ ；

(3)、如果 $△ A B C$ 与 $△ B C D$ 全等，请写出满足条件的所有点D的坐标（点D不与点A重合）．

查看试题解析