湘教版数学八年级下学期 3.2 简单图形的坐标表示同步分层训练提升题
试卷更新日期:2024-03-26 类型:同步测试
一、选择题
-
1. 已知轴,且点的坐标为 , 点的坐标为 , 则点的纵坐标为( )A、3 B、4 C、0 D、-32. 如图,点A(8,0),C(-2,0),以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为( )
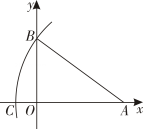 A、(0,5) B、(5,0) C、(6,0) D、(o,6)3. 如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标可能有( )个.
A、(0,5) B、(5,0) C、(6,0) D、(o,6)3. 如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标可能有( )个. A、1个 B、2个 C、3个 D、4个4. 已知等腰三角形ABC,建立适当的平面直角坐标系后,其三个顶点的坐标分别为 , , 则下列关于该三角形三边关系的说法中正确的是( )A、 B、 C、 D、5. 如图,在正方形中,是坐标原点,点的坐标为 , 则点的坐标是( )
A、1个 B、2个 C、3个 D、4个4. 已知等腰三角形ABC,建立适当的平面直角坐标系后,其三个顶点的坐标分别为 , , 则下列关于该三角形三边关系的说法中正确的是( )A、 B、 C、 D、5. 如图,在正方形中,是坐标原点,点的坐标为 , 则点的坐标是( ) A、 B、 C、 D、6. 如图,在平面直角坐标系中,点A、B的坐标分别是(﹣3,0),(0,6),若△AOB≌△CDA,则点D的坐标是( )
A、 B、 C、 D、6. 如图,在平面直角坐标系中,点A、B的坐标分别是(﹣3,0),(0,6),若△AOB≌△CDA,则点D的坐标是( ) A、(﹣9,0) B、(﹣6,0) C、(0,﹣9) D、(﹣12,0)7. 平面直角坐标系中,已知▱ABCD的三个顶点坐标分别是A(m,n),B(2,﹣1),C(﹣m,﹣n),则点D的坐标是( )A、(﹣2,1) B、(﹣2,﹣1) C、(﹣1,﹣2) D、(﹣1,2)8. 我们知道,四边形具有不稳定性,如图,在平面直角坐标系中,边长为2的正方形的边在x轴上,的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点处,则点C的对应点的坐标为( )
A、(﹣9,0) B、(﹣6,0) C、(0,﹣9) D、(﹣12,0)7. 平面直角坐标系中,已知▱ABCD的三个顶点坐标分别是A(m,n),B(2,﹣1),C(﹣m,﹣n),则点D的坐标是( )A、(﹣2,1) B、(﹣2,﹣1) C、(﹣1,﹣2) D、(﹣1,2)8. 我们知道,四边形具有不稳定性,如图,在平面直角坐标系中,边长为2的正方形的边在x轴上,的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点处,则点C的对应点的坐标为( )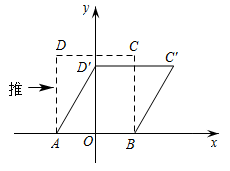 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 在平面直角坐标系中,若点M(1,x)与点N(1,3)之间的距离是5,则x的值是 .10. 如图,在△ABC中, , , , , 当点B在第四象限时,点B的坐标为 .
 11. 如图,BC⊥AB,则图中阴影部分的面积为 .
11. 如图,BC⊥AB,则图中阴影部分的面积为 . 12. 在平面直角坐标系中,长方形按如图所示放疽,是AD的中点,且、、的坐标分别为 , , , 点是BC上的动点,当是腰长为5的等腰三角形时,则点的坐标为 .
12. 在平面直角坐标系中,长方形按如图所示放疽,是AD的中点,且、、的坐标分别为 , , , 点是BC上的动点,当是腰长为5的等腰三角形时,则点的坐标为 .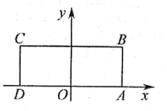
三、解答题
-
13. 在中, , , 直角顶点C在x轴上,一锐角顶点B在y轴上.
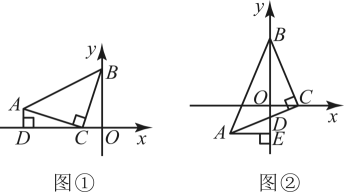 (1)、如图①,作轴于点D . 若点C的坐标是 , 点B的坐标是 , 求点A的坐标;(2)、如图②,直角边BC在两坐标轴上滑动,若y轴恰好平分 , AC与y轴交于点D , 过点A作轴于点E . 求证: .14. 如图,在平面直角坐标系中,与全等,其中A,B,C的对应顶点分别为D,E,F,且 . 若A点的坐标为 , B,C两点的纵坐标均为 , D,E两点在y轴上.
(1)、如图①,作轴于点D . 若点C的坐标是 , 点B的坐标是 , 求点A的坐标;(2)、如图②,直角边BC在两坐标轴上滑动,若y轴恰好平分 , AC与y轴交于点D , 过点A作轴于点E . 求证: .14. 如图,在平面直角坐标系中,与全等,其中A,B,C的对应顶点分别为D,E,F,且 . 若A点的坐标为 , B,C两点的纵坐标均为 , D,E两点在y轴上. (1)、求证:等腰两腰上的高相等;(2)、求两腰上高线的长;(3)、求的高线的长.
(1)、求证:等腰两腰上的高相等;(2)、求两腰上高线的长;(3)、求的高线的长.四、综合题

