2023-2024学年湘教版初中数学九年级下学期 4.3 用频率估计概率同步分层训练培优题
试卷更新日期：2024-03-26 类型：同步测试
一、选择题
-
1. 下列说法正确的是（ ）A、某彩票的中奖概率是5%，那么买100张彩票一定有5张中奖 B、某次试验投掷次数是500，计算机记录“钉尖向上”的次数是308，则该次试验“钉尖向上”的频率是0.616 C、当试验次数很大时，概率稳定在频率附近 D、试验得到的频率与概率不可能相等2. 某人做投硬币试验时，投掷 次，正面朝上 次（即正面朝上的频率 ），则下列说法正确的是（ ）A、 一定等于 B、 一定不等于 C、多投一次， 更接近 D、投掷次数逐渐增加， 稳定在 附近3. 某收费站在2小时内对经过该站的机动车统计如下：
类型
轿车
货车
客车
其他
数量（辆）
36
24
8
12
若有一辆机动车将经过这个收费站，利用上面的统计估计它是轿车的概率为（ ）
A、 B、 C、 D、4. 下列说法正确的是（ ）A、连续抛一枚硬币n次，当n越来越大时，出现正面朝上的频率会越来越稳定于0.5 B、连续抛一枚硬币50次，出现正面朝上的次数是25次 C、连续三次掷一颗骰子都出现了奇数，则第四次出现的数一定是偶数 D、某地发行一种福利彩票，中奖概率为1%，买这种彩票100张一定会中奖5. 盒子中有白色乒乓球8个和黄色乒乓球若干个，为求得盒中黄色乒乓球的个数，某同学进行了如下实验：每次摸出一个乒乓球记下它的颜色，如此重复360次，摸出白色乒乓球90次，则黄色乒乓球的个数估计为（ ）A、90个 B、24个 C、70个 D、32个6. 在一个不透明的布袋中，红球、黑球、白球共有若干个，除颜色外，形状、大小、质地等完全相同．小新从布袋中随机摸出一球，记下颜色后放回布袋中，摇匀后再随机摸出一球，记下颜色，……，如此大量摸球实验后，小新发现从中摸出红球的频率稳定于20%，摸出黑球的频率稳定于50%．对此实验，他总结出下列结论：①若进行大量摸球实验，摸出白球的频率应稳定于30%；②若从布袋中任意摸出一个球，该球是黑球的概率最大；③若再摸球100次，必有20次摸出的球是红球．其中说法正确的是（ ）
A、①②③ B、①② C、①③ D、②③7. 某射击运动员在同一条件下的射击成绩记录如下：射击次数
20
80
100
200
400
1000
“射中8环以上”的次数
18
68
82
168
327
823
“射中8环以上”的频率（结果保留两位小数）
0.90
0.85
0.82
0.84
0.82
0.82
根据频率的稳定性，估计这名运动员射击一次时“射中8环以上”的概率约是（ ）
A、0.90 B、0.82 C、0.85 D、0.848. 某林业局将一种树苗移植成活的情况绘制成如下折线统计图，由此可估计这种树苗移植成活的概率约为（ ）.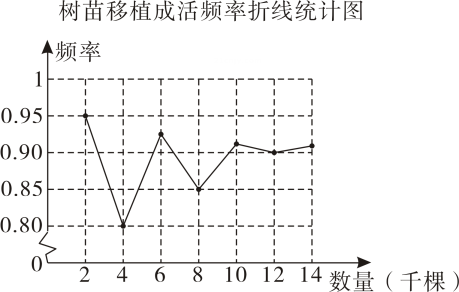
A、0.95 B、0.90 C、0.85 D、0.80二、填空题
-
9. 在一个不透明的盒子中有25个除颜色外均相同的小球，每次摸球前先将盒中的球摇匀，随机摸出一个球记下颜色后再放回盒中，通过大量重复摸球试验后，发现摸到白球的频率稳定于0.4，由此可估计盒子中白球的个数约为 ．10. 为估计可可西里某区域内藏羚羊的数量，先捕捉20只给它们作上标记，然后放回；待有标志的藏羚羊完全混合于藏羚羊群后，第二次捕捉40只，发现其中2只有标记，从而估计该区域有藏羚羊约有只．11. 某射手在同一条件下进行射击，结果如下表所示：
射击次数
10
20
50
100
200
500
…
击中靶心次数
8
19
44
92
178
455
…
击中靶心频率
…
请将上面的表格补充完整.由此表推断这位射手射击1次，击中靶心的概率约是.
12. 一口袋中有6个红球和若干个白球，除颜色外均相同，从口袋中随机摸出一球，记下颜色，再把它放回口袋中摇匀．重复上述实验共300次，其中120次摸到红球，则口袋中大约有个白球．
三、解答题
-
13. 为了考察甲、乙两种成熟期小麦的株高长势情况，现从中随机抽取6株，并测得它们的株高（单位：cm）如下表所示：
甲
63
66
63
61
64
61
乙
63
65
60
63
64
63
（Ⅰ）请分别计算表内两组数据的方差，并借此比较哪种小麦的株高长势比较整齐？
（Ⅱ）现将进行两种小麦优良品种杂交实验，需从表内的甲、乙两种小麦中，各随机抽取一株进行配对，以预估整体配对情况，请你用列表法或画树状图的方法，求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率．
14. 甲、乙两位同学做抛骰子（均匀正方体形状）实验，他们共抛了60次，出现向上点数的次数如表：向上点数
1
2
3
4
5
6
出现次数
8
10
7
9
16
10
（1）计算出现向上点数为6的频率．
（2）丙说：“如果抛600次，那么出现向上点数为6的次数一定是100次．”请判断丙的说法是否正确并说明理由．
（3）如果甲乙两同学各抛一枚骰子，求出现向上点数之和为3的倍数的概率．
四、综合题
-
15. 在一个不透明的盒子里装有颜色不同的黑、白两种球共40个，小颖做摸球试验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是“摸到白色球”的频率折线统计图.
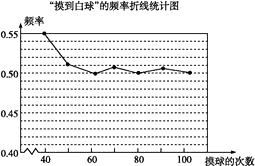(1)、请估计：当n足够大时，摸到白球的频率将会稳定在(精确到0.01)，假如你摸一次，你摸到白球的概率为；
(2)、试估算盒子里白、黑两种颜色的球各有多少个?
(3)、在(2)条件下如果要使摸到白球的概率为 ，需要往盒子里再放入多少个白球?
16. 某生活小区鲜奶店每天以每瓶3元的价格从奶场购进优质鲜奶，然后以每瓶6元的价格出售，如果当天卖不完，剩余的只有倒掉．店主记录了30天的日需求量（单位：瓶），整理得下表：日需求量
26
27
28
29
30
频数
5
8
7
6
4
(1)、求这30天内日需求量的众数；
(2)、假设鲜奶店在这30天内每天购进28瓶，求这30天的日利润（单位：元）的平均数；(3)、以30记录的各需求量的频率作为各需求是发生的概率．若鲜奶店每天购进28瓶，求在这记录的30天内日利润不低于81元的概率．
17. 某射击运动员在相同条件下的射击160次，其成绩记录如下：设计次数
20
40
60
80
100
120
140
160
射中九环以上的次数
15
33
____
63
79
97
111
130
射中九环以上的频率
0.75
0.83
0.80
0.79
0.79
____
0.79
0.81
(1)、根据上表中的信息将两个空格的数据补全（射中9环以上的次数为整数，频率精确到0.01）；(2)、根据频率的稳定性，估计这名运动员射击一次时“射中9环以上”的概率（精确到0.1），并简述理由．