2023-2024学年湘教版初中数学九年级下学期 4.3 用频率估计概率同步分层训练基础题

试卷更新日期：2024-03-26 类型：同步测试

进入出卷网下载

一、选择题

1. 一个盒子中装有a个白球和3个红球（除颜色外完全相同），若每次将球充分搅匀后，任意摸出1个球记下颜色再放回盒子，通过大量重复试验后，发现摸到白球的频率稳定在80%左右，则a的值约为（）

A、9 B、12 C、15 D、18

查看试题解析
2. 在一个不透明的盒子中，红色、白色、黑色的球共有40个，除颜色外其他完全相同，老师在课堂上组织同学通过多次试验后发现其中摸到红色、白色的频率基本稳定在45%和15%，则盒子中黑色球的个数可能是（　　）.

A、16 B、18 C、20 D、22

查看试题解析
3. 在一个不透明的口袋里，装了只有颜色不同的黄球、白球若干只.某小组做摸球试验：将球搅匀后从中随机摸出一个，记下颜色，再放回袋中，不断重复.下表是活动中的一组数据，则摸到黄球的概率约是（）
摸球的
次数n
100
150
200
500
800
1 000
摸到黄球
的次数m
52
69
96
266
393
507
摸到黄球
的频率 $\frac{m}{n}$
0.52
0.46
0.48
0.532
0.491
0.507

A、0.4 B、0.5 C、0.6 D、0.7

查看试题解析
4. 二维码越来越普及到人们生活的方方面面，成为了广大民众生活中不可或缺的一部分.如图是小刚在面积为16的正方形纸片上打印的二维码，为了估计黑色阴影部分的面积，他在纸内随机掷点，经过大量实验，发现点落在黑色阴影的频率稳定在0.6左右，则据此估计此二维码中黑色阴影的面积为（）

A、9.6 B、0.6 C、6.4 D、0.4

查看试题解析
5. 一个口袋中有红球、黄球共20个，这些除颜色外都相同，将口袋中的球搅拌均匀，从中随机摸出一球，记下颜色后再放回口袋，不断重复这一过程，共摸了200次，发现其中有161次摸到红球．则这个口袋中红球数大约有（　　）

A、4个 B、10个 C、16个 D、20个

查看试题解析
6. 在一个不透明的盒子中装有n个小球，它们除了颜色不同外，其余都相同，其中有4个白球，每次试验前，将盒子中的小球摇匀，随机摸出一个球记下颜色后再放回盒中．大量重复上述试验后发现，摸到白球的频率稳定在0.4，那么可以推算出n大约是（　　）

A、10 B、14 C、16 D、40

查看试题解析
7. 甲、乙两名同学在一次用频率去估计概率的试验中统计了某一结果出现的频率，绘出的统计图如图所示，则符合这一结果的试验可能是（）

A、从一个装有 $2$ 个白球和 $1$ 个红球的袋子中任取一球，取到红球 B、掷一枚正六面体的骰子，出现 $1$ 点 C、抛一枚硬币，出现正面 D、任意写一个整数，它能被 $2$ 整除

查看试题解析
8. 在一个不透明的口袋中，装有除颜色外其他都相同的4个白球和n个黄球，某同学进行如下试验：从袋中随机摸出1个球记下它的颜色，放回、摇匀，为一次摸球试验，记录摸球的次数与摸出白球的次数的列表如下：
摸球试验的次数
100
200
500
1000
摸出白球的次数
21
39
102
199
根据列表可以估计出n的值为（）

A、16 B、4 C、20 D、24

查看试题解析

二、填空题

9. 某种绿豆在相同条件下发芽试验的结果如下
每批粒数 $n$
100
500
1 000
1 500
2 000
3 000
发芽的频数 $m$
94
466
928
1 396
1 858
2 790
发芽的频率 $\frac{m}{n}$ （精确到0.001）
0.940
0.932
0.928
0.931
0.929
0.930
根据上表估计，这种绿豆发芽的概率是．（精确到0.01）

查看试题解析
10. 某种麦粒在相同条件下进行发芽试验，结果如下表所示：
试验的麦粒数 $n$
$100$
$200$
$500$
$1000$
$2000$
$5000$
发芽的麦粒数 $m$
$93$
$188$
$473$
$954$
$1906$
$4748$
发芽的频率 $\frac{m}{n}$
$0.93$
$0.94$
$0.946$
$0.954$
$0.953$
$0.9496$
则任取一粒麦粒，估计它能发芽的概率约为．（结果精确到 $0.01$ ）

查看试题解析
11. 为了估计抛掷同一枚瓶盖落地后凸面向上的概率，小明做了大量重复试验. 经过统计得到凸面向上的次数为 450 次，凸面向下的次数为 550 次，由此可估计抛郑瓶盖落地后凸面向上的概率约为.

查看试题解析
12. 在一个不透明的袋中装有若干个红球和4个黑球，每个球除颜色外完全相同．摇匀后从中摸出一个球，记下颜色后再放回袋中．不断重复这一过程，共摸球100次．其中有40次摸到黑球，估计袋中红球的个数是．

查看试题解析
13. 一年之计在于春，为保障春播任务顺利完成，科研人员对某玉米种子在相同条件下发芽情况进行试验，结果如表：
每批粒数n
500
800
1000
2000
3000
发芽的频数m
463
768
948
1901
2851
发芽的频率 $\frac{m}{n}$
0.926
0.96
0.948
0.951
0.950
那么这种玉米发芽的概率是．（结果精确到0.01）

查看试题解析

三、解答题

14. 在一个不透明的口袋里装有红、白两种颜色的球共4个，它们除颜色外其余都相同．某学习小组做摸球实验，将球摚匀后从中随机摸出一个球，记下颜色，再把它放回袋中，不断重复，下表是活动进行中的一组统计数据：
摸球的次数
500
1000
1500
2000
2500
3000
摸到白球的频率
0.748
0.751
0.754
0.747
0.750
0.749

(1)、当摸球次数很大时，摸到白球的频率将会接近．（精确到 $0.01$ ）

(2)、试估算口袋中白球有个．

(3)、现有另一个不透明的口袋中装有一红一白两个球，它们除颜色外其余都相同．一学生从两个口袋中各摸出一个球，请利用画树状图或列表的方法计算这两个球颜色相同的概率．

查看试题解析

15. 某水果公司新进了

10000

千克柑橘，销售人员首先从所有的柑橘中随机地抽取若干柑橘，进行了“柑橘损坏率”统计，并把获得的数据记录在下表中：

柑橘总质量（ $n$ /千克）	损坏柑橘质量（ $m$ /千克）	柑橘损坏的频率（ $\frac{m}{n}$ ）
$50$	$5.50$	$0.110$
$100$	$10.50$	$0.105$
$150$	$15.15$	$0.101$
$200$	$19.42$	$0.097$
$250$	$24.35$	$0.097$
$300$	$30.93$	$a$
$350$	$35.32$	$0.101$
$400$	$39.24$	$b$
$450$	$44.57$	$0.099$
$500$	$51.54$	$c$

(1)、写出

a =

▲

b =

▲

c =

▲ （精确到

0.001

）.

(2)、估计这批柑橘的损坏概率为 ▲ （精确到

0.1

）.

(3)、该水果公司以

2

元每千克的成本进的这批柑橘，公司希望这批柑橘能够获得利润

5000

元，那么在出售柑橘（已去掉损坏的柑橘）时，求出每千克大约定价为多少元时比较合适（精确到

0.1

）.

查看试题解析

四、综合题

16. 为某批篮球的质量检验结果如下：

抽取的篮球数n	100	200	400	600	800	1000	1200
优等品的频数m	93	192	380	561	b	941	1128
优等品的频率m/n	$\begin{array}{l} 0.93 \end{array}$	a	$\begin{array}{l} 0.95 \end{array}$	$\begin{array}{l} 0.935 \end{array}$	$\begin{array}{l} 0.94 \end{array}$	$\begin{array}{l} 0.941 \end{array}$	$\begin{array}{l} 0.94 \end{array}$

(1)、此次调查方式为（填“普查”或“抽样调查”）；

(2)、补全表中数据：

a =

，

b =

；

(3)、从这批篮球中，任意抽取的一只篮球是优等品的概率的估计值为（精确到

0.01

）．

查看试题解析

17.
在一个不透明的盒子里装有颜色不同的黑、白两种球共40个，小颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是“摸到白色球”的频率折线统计图．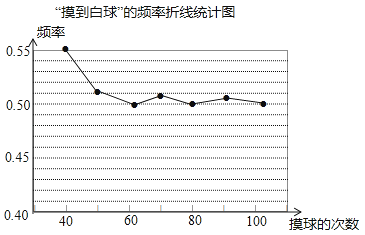

(1)、请估计：当n很大时，摸到白球的概率将会接近　（精确到0.01），假如你摸一次，你摸到白球的概率为

(2)、试估算盒子里白、黑两种颜色的球各有多少个？

(3)、在（2）条件下如果要使摸到白球的概率为 $\frac{3}{5}$ ，需要往盒子里再放入多少个白球？

查看试题解析

摸球试验的次数	100	200	500	1000
摸出白球的次数	21	39	102	199

每批粒数 $n$	100	500	1 000	1 500	2 000	3 000
发芽的频数 $m$	94	466	928	1 396	1 858	2 790
发芽的频率 $\frac{m}{n}$ （精确到0.001）	0.940	0.932	0.928	0.931	0.929	0.930

试验的麦粒数 $n$	$100$	$200$	$500$	$1000$	$2000$	$5000$
发芽的麦粒数 $m$	$93$	$188$	$473$	$954$	$1906$	$4748$
发芽的频率 $\frac{m}{n}$	$0.93$	$0.94$	$0.946$	$0.954$	$0.953$	$0.9496$

每批粒数n	500	800	1000	2000	3000
发芽的频数m	463	768	948	1901	2851
发芽的频率 $\frac{m}{n}$	0.926	0.96	0.948	0.951	0.950

摸球的次数	500	1000	1500	2000	2500	3000
摸到白球的频率	0.748	0.751	0.754	0.747	0.750	0.749