湘教版数学九年级下学期 3.2 直棱柱、圆锥的侧面展开图同步分层训练培优题
试卷更新日期:2024-03-26 类型:同步测试
一、选择题
-
1. 如图是几何体的展开图,这个几何体是( )
 A、圆柱 B、三棱锥 C、四棱柱 D、三棱柱2. 如图,下面每一组图形都由四个等边三角形组成,其中可以折叠成三棱锥的是( )
A、圆柱 B、三棱锥 C、四棱柱 D、三棱柱2. 如图,下面每一组图形都由四个等边三角形组成,其中可以折叠成三棱锥的是( )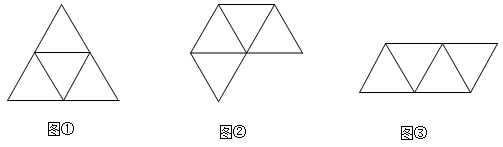 A、仅图① B、图①和图② C、图②和图③ D、图①和图③3.
A、仅图① B、图①和图② C、图②和图③ D、图①和图③3.如图,是某种几何体表面展开图的图形.这个几何体是( )
 A、圆锥 B、球 C、圆柱 D、棱柱4.
A、圆锥 B、球 C、圆柱 D、棱柱4.如图是一个正方体的包装盒的展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( )
 A、﹣1,﹣2,1 B、﹣1,1,﹣2 C、﹣2,﹣1,1 D、1,﹣1,﹣25.
A、﹣1,﹣2,1 B、﹣1,1,﹣2 C、﹣2,﹣1,1 D、1,﹣1,﹣25.一个正方体的6个面分別标有“E”、“F”、“G”、“H”、“M”、“N”中的一个字母,如图表示的是该正
方体3种不同的摆法,当“E”在右面时,左面的字母是( )
 A、G B、H C、M D、N6.
A、G B、H C、M D、N6.如图1,是一个正方体的展开图,小正方体从图2所示的位置依次翻滚到第1格、第2格、第3格,这时小正方体朝上面的字是( )
 A、真 B、精 C、彩 D、届7. 图①是正方体的平面展开图,六个面的点数分别为1点、2点、3点、4点、5点、6点,将点数朝外折叠成一枚正方体骰子,并放置于水平桌面上,如图②所示,若骰子初始位置为图②所示的状态,将骰子向右翻滚 ,则完成1次翻转,此时骰子朝下一面的点数是2,那么按上述规则连线完成2次翻折后,骰子朝下一面的点数是3点;连续完成2019次翻折后,骰子朝下一面的点数是( )
A、真 B、精 C、彩 D、届7. 图①是正方体的平面展开图,六个面的点数分别为1点、2点、3点、4点、5点、6点,将点数朝外折叠成一枚正方体骰子,并放置于水平桌面上,如图②所示,若骰子初始位置为图②所示的状态,将骰子向右翻滚 ,则完成1次翻转,此时骰子朝下一面的点数是2,那么按上述规则连线完成2次翻折后,骰子朝下一面的点数是3点;连续完成2019次翻折后,骰子朝下一面的点数是( ) A、2 B、3 C、4 D、58. 如图,一个正六棱柱的表面展开后恰好放入一个矩形内,把其中一部分图形挪动了位置,发现矩形的长留出5cm,宽留出1cm,则该六棱柱的侧面积是( )
A、2 B、3 C、4 D、58. 如图,一个正六棱柱的表面展开后恰好放入一个矩形内,把其中一部分图形挪动了位置,发现矩形的长留出5cm,宽留出1cm,则该六棱柱的侧面积是( )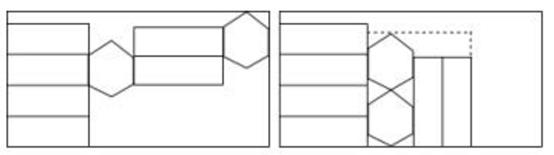 A、(108- )cm2 B、(108- )cm2 C、(54- )cm2 D、(54- )cm2
A、(108- )cm2 B、(108- )cm2 C、(54- )cm2 D、(54- )cm2二、填空题
-
9. 如图,该图形折叠成正方体后,与“沉”字相对的字是 .
 10. 杭州亚运会于2023年10月顺利落幕,中国队获金牌和奖牌榜双第一,如图是一个正方体的表面展开图,与“亚”字相对面上的汉字是 .
10. 杭州亚运会于2023年10月顺利落幕,中国队获金牌和奖牌榜双第一,如图是一个正方体的表面展开图,与“亚”字相对面上的汉字是 . 11. 下列图形中是正方体的平面展开图的有(填序号).
11. 下列图形中是正方体的平面展开图的有(填序号).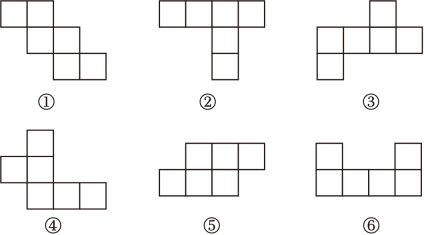 12. 如图是一个正方体形状纸盒的展开图,将其折成正方体后,相对面上的两数互为相反数,则 .
12. 如图是一个正方体形状纸盒的展开图,将其折成正方体后,相对面上的两数互为相反数,则 .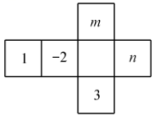 13. 已知一个不透明的正方体的六个面上分别写着1至6六个数字,如图是我们能看到的三种情况,那么4所在面的对面是.
13. 已知一个不透明的正方体的六个面上分别写着1至6六个数字,如图是我们能看到的三种情况,那么4所在面的对面是.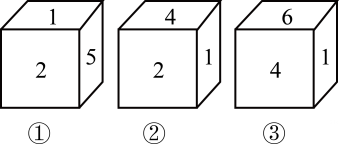
三、解答题
-
14.
小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
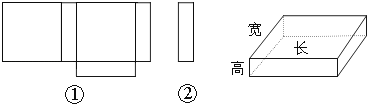
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
15. 如图是某长方体包装盒的展开图.设长方体的高为x cm.根据图中具体的数据,解答下列问题: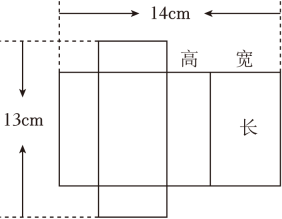 (1)、用含x的式子表示这个长方体的长和宽;(2)、若长方体盒子的长比宽多3cm,求这种长方体包装盒的体积;(3)、满足(2)中条件的长方体的表面展开图还有不少,你能画出一个使外围周长最大的表面展开图吗?请画出这个表面展开图,并求出它的外围周长.
(1)、用含x的式子表示这个长方体的长和宽;(2)、若长方体盒子的长比宽多3cm,求这种长方体包装盒的体积;(3)、满足(2)中条件的长方体的表面展开图还有不少,你能画出一个使外围周长最大的表面展开图吗?请画出这个表面展开图,并求出它的外围周长.四、综合题
-
16. 综合与实践:制作一个无盖长方形盒子.
用一张正方形的纸片制成一个如图的无盖长方体纸盒.如果我们按照如图所示的方式,将正方形的四个角减掉四个大小相同的小正方形,然后沿虚线折起来,就可以做成一个无盖的长方体盒子.
 (1)、如果原正方形纸片的边长为a cm,剪去的正方形的边长为b cm,则折成的无盖长方体盒子的高为cm,底面积为cm2 , 请你用含a,b的代数式来表示这个无盖长方体纸盒的容积cm3;(2)、如果a=20cm,剪去的小正方形的边长按整数值依次变化,即分别取1cm,2cm,3cm,4cm,5cm,6cm,7cm,8cm,9cm,10cm时,折成的无盖长方体的容积分别是多少?请你将计算的结果填入下表;
(1)、如果原正方形纸片的边长为a cm,剪去的正方形的边长为b cm,则折成的无盖长方体盒子的高为cm,底面积为cm2 , 请你用含a,b的代数式来表示这个无盖长方体纸盒的容积cm3;(2)、如果a=20cm,剪去的小正方形的边长按整数值依次变化,即分别取1cm,2cm,3cm,4cm,5cm,6cm,7cm,8cm,9cm,10cm时,折成的无盖长方体的容积分别是多少?请你将计算的结果填入下表;剪去正方形的
边长/cm
1
2
3
4
5
6
7
8
9
10
容积/cm3
324
512
500
384
252
128
36
0
(3)、观察绘制的统计表,你发现,随着减去的小正方形的边长的增大,所折无盖长方体盒子的容积如何变化?( )A、一直增大 B、一直减小 C、先增大后减小 D、先减小后增大(4)、分析猜想当剪去图形的边长为时,所得的无盖长方体的容积最大,此时无盖长方体的容积是cm3.(5)、对(2)中的结果,你觉得表格中的数据还有什么要改进的地方吗?17. 仔细阅读,解答下列问题(1)、有一长方体的食物包装纸盒如图(1),已知长方体的底面长为12,宽为9,高为5,一只蚂蚁想从底面A处爬到B处去吃食物,请问:蚂蚁爬行的最短距离是多少? (2)、如图(2),圆柱形容器的高为1.2米,底面周长为1米,在容器内壁高容器底部0.3米的点B处有一只蚊子,此时一只壁虎正好在容器外壁高容器上沿0.3米与蚊子相对的点A处,求壁虎捕捉到蚊子的最短路程是多少?(容器厚度忽略不计)
(2)、如图(2),圆柱形容器的高为1.2米,底面周长为1米,在容器内壁高容器底部0.3米的点B处有一只蚊子,此时一只壁虎正好在容器外壁高容器上沿0.3米与蚊子相对的点A处,求壁虎捕捉到蚊子的最短路程是多少?(容器厚度忽略不计)