2023-2024学年湘教版初中数学九年级下学期 3.1 投影同步分层训练提升题
试卷更新日期：2024-03-26 类型：同步测试
一、选择题
-
1. 如图所示，表示两棵小树在同一时刻阳光下的影子的图形可能是（ ）A、
B、
C、
D、
2. 下列四幅图形中，表示两棵圣诞树在同一时刻阳光下的影子的图形可能是（ ）A、
B、
C、
D、
3. 如图，在某一时刻测得1米长的竹竿竖直放置时影长1.2米，在同一时刻旗杆AB的影长不全落在水平地面上，有一部分落在楼房的墙上，他测得落在地面上影长为BD＝9.6米，留在墙上的影长CD＝2米，则旗杆的高度（ ）
A、12米 B、10.2米 C、10米 D、9.6米4. 如图，AB表示一个窗户的高，AM和BN表示射入室内的光线，窗户的下端到地面距离BC＝1米，已知某一时刻BC在地面的影长CN＝1.5米，AC在地面的影长CM＝4.5米，则AB高为（ ）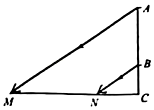
A、3.5 B、2 C、1.5 D、2.55. 如图，在直角坐标系中，点P(2，2)是一个光源．木杆AB两端的坐标分别为(0，1)，(3，1)．则木杆AB在x轴上的投影长为（ ）
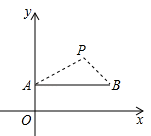A、3 B、4 C、5 D、66. 如图，有一路灯杆AP，路灯P距地面4.8m，身高1.6m的小明站在距A点4.8m的点D处，小明的影子为DE，他沿射线DA走2.4m到达点B处，小明的影子为BC，此时小明影子的长度（ ）
A、增长了1m B、缩短了1m C、增长了1.2m D、缩短了1.2m7. 如图，小聪和他同学利用影长测量旗杆的高度，当1米长的直立的竹竿的影长为1.5米时，此时测得旗杆落在地上的影长为12米，落在墙上的影长为2米，则旗杆的实际高度为（ ）
A、8米 B、10米 C、18米 D、20米8. 如图，身高1.5米的小明（AB）在太阳光下的影子AG长1.8米，此时，立柱CD的影子一部分是落在地面的CE，一部分是落在墙EF上的EH.若量得米，米，则立柱CD的高为（ ）.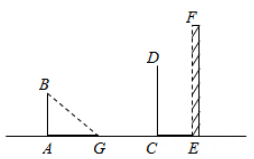
A、2.5m B、2.7m C、3m D、3.6m二、填空题
-
9. 如图，已知路灯离地面的高度AB为4.8m，身高为1.6 m的小明站在D处的影长DC为2 m，那么此时小明离路灯杆AB的距离BD为m
10. 在阳光下，高为6m的旗杆在地面上的影长为4m，在同一时刻，测得附近一座建筑物的影长为 ， 则这座建筑物的高度为m．11. 如图，物体在灯泡发出的光照射下形成的影子是投影.（填“平行”或“中心”）.
12. 一块直角三角形板 ， ， ， ， 测得边的中心投影长为 ， 则长为.
13. 如图是某风车示意图，其相同的四个叶片均匀分布，水平地面上的点M在旋转中心O的正下方，某一时刻，太阳光线恰好垂直照射叶片、 ， 此时各叶片影子在点M右侧成线段 ． 测得 ， ， 垂直于地面的木棒与影子的比为 ． 则点O、M之间的距离等于m；
三、解答题
-
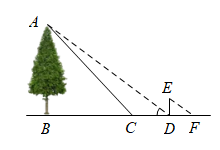
14. “创新实践”小组想利用所学知识测量大树的高度，因大树底部有障碍物，无法直接测量到大树底部的距离，他们制定了如下的测量方案：如图所示，小丽通过调整测角仪的位置，在大树周围的点C处用测角仪测得大树顶部A的仰角为（测角仪的高度忽略不计）.接着，小丽沿着方向向前走3米（即米），到达大树在太阳光下的影子末端D处，此时小明测得小丽在太阳光下的影长为2米.已知小丽的身高为1.5米，B、C、D、F四点在同一直线上， ， 求这棵大树的高度.
15. 据说，在距今2500多年前，古希腊数学家就已经较准确地测出了埃及金字塔的高度，操作过程大致如下：如图所示，设AB是金字塔的高，在某一时刻，阳光照射下的金字塔在底面上投下了一个清晰的阴影，塔顶A的影子落在地面上的点C处，金字塔底部可看作方正形FGHI，测得正方形边长FG长为160米，点B在正方形的中心，BC与金字塔底部一边垂直于点K，与此同时，直立地面上的一根标杆DO留下的影子是OE，射向地面的太阳光线可看作平行线（AC∥DE），此时测得标杆DO长为1.2米，影子OE长为2.7米，KC长为250米，求金字塔的高度AB及斜坡AK的坡度（结果均保留四个有效数字）
四、综合题
