2023-2024学年湘教版初中数学九年级下学期 3.1 投影同步分层训练基础题
试卷更新日期：2024-03-26 类型：同步测试
一、选择题
-
1. 一个矩形木框在地面上形成的投影不可能是（ ）A、
B、
C、
D、
2. 李华的弟弟拿着一个菱形木框在阳光下玩耍，李华发现菱形木框在阳光照射下，在地面上形成了各种图形的影子，但以下一种图形始终没有出现，没有出现的图形是（ ）A、
B、
C、
D、
3. 如图，身高为1.6 m的某学生想测量学校旗杆的高度，当他站在C处时，他头顶端的影子正好与旗杆顶端的影子重合，并测得AC＝2 m，AB＝10 m，则旗杆的高度是（ ）
A、6.4m B、7m C、8m D、9m4. 如图，正方形纸板的一条对角线重直于地面，纸板上方的灯（看作一个点）与这条对角线所确定的平面垂直于纸板，在灯光照射下，正方形纸板在地面上形成的影子的形状可以是（ ）
A、
B、
C、
D、
5. 晚上，人在马路上走过一盏路灯的过程中，其影子长度的变化情况是（ ）A、先变短后变长 B、先变长后变短 C、逐渐变短 D、逐渐变长6. 如图，小明周末晚上陪父母在马路上散步，他由灯下A处前进4米到达B处时，测得影子长为1米，已知小明身高1.6米，他若继续往前走4米到达D处，此时影子长为（ ）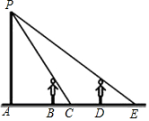
A、1米 B、2米 C、3米 D、4米7. 如图，哪一个是太阳光下形成的影子？（ ）A、
B、
C、
D、
8. 如图，小颖身高为 ，在阳光下影长 ，当她走到距离墙角（点 ） 的 处时，她的部分影子投射到墙上，则投射在墙上的影子 的长度为（ ）
A、 B、 C、 D、二、填空题
-
9. 早在多年前的宋朝，手影就已经作为民间一种有趣的游戏而存在．诗人释惠明在《手影戏》中写到：“三尺生绡作戏台，全凭十指送诙谐．有时明月灯窗下，一笑还从掌握来”．手影戏全凭手影艺人的十指借光弄影，表演各色人物、花草虫鱼、飞禽走兽甚至是寓言故事．如图，手影戏中的手影属于（填“平行投影”或“中心投影”）．
10. 如图，地面上的A处有一支燃烧的蜡烛（长度不计），一个人在A与墙BC之间运动，则他在墙上的投影长度随着他离墙的距离变小而（填“变大”、“变小”或“不变”）．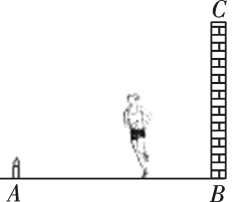
11. 为测量广场上一棵树的高度，数学小组在阳光下测得广场上一根6m高的灯柱的影长为3m，在同一时刻，他们测得树的影长为2m，则该树的高度为 m．12. 如图，在平面直角坐标系中，点光源位于处，木杆两端的坐标分别为 ， 则木杆在轴上的影长为 ．
13. 《孙子算经》是中国古代重要的数学著作，其中有首歌谣：“今有竿不知其长，量得影长一百五十寸，立一标杆，长一十五寸，影长五寸，问竿长几何？”．其意思是：“如图，有一根竹竿不知道有多长，量出它在太阳下的影子长150寸，同时立一根15寸的小标杆 ， 它的影子长5寸，则竹竿的长为多少？”．答：竹竿的长为寸．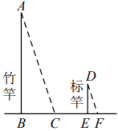
三、解答题
-
14. 已知：如图，和是直立在地面上的两根立柱， ， 某一时刻，在阳光下的投影 ．
(1)、请你在图中画出此时在阳光下的投影，并简述画图步骤和说明作图依据了太阳光线的哪一性质；(2)、在测量的投影长时，同时测出在阳光下的投影长为 ， 请你计算的长．15. 小明和几位同学做手的影子游戏时，发现对于同一物体，影子的大小与光源到物体的距离有关因此，他们认为：可以借助物体的影子长度计算光源到物体的位置于是，他们做了以下尝试．
(1)、如图 ， 垂直于地面放置的正方形框架 ， 边长为 ， 在其上方点处有一灯泡，在灯泡的照射下，正方形框架的横向影子 ， 的长度和为那么灯泡离地面的高度为多少．(2)、不改变图中灯泡的高度，将两个边长为的正方形框架按图摆放，请计算此时横向影子 ， 的长度和为多少？四、综合题
-
16.
已知，如图，AB和DE是直立在地面上的两根立柱AB=6m，某一时刻AB在太阳光下的投影BC=3m．
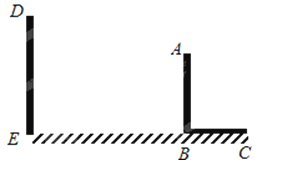(1)、请你在图中画出此时DE在太阳光下的投影EF；(2)、在测量AB的投影时，同时测量出DE在太阳光下的投影EF长为6m，请你计算DE的长．17. 如图，小明为了方便出行，在家门口安装了两盏路灯，灯泡分别位于A、B两点处，两盏路灯之间有一棵树（用图中CD表示），已知树CD在灯泡A的照射下，其影子末端位于点E处；在灯泡B的照射下，其影子末端位于点F处，D、E、F三点在一条直线上，且CD⊥EF于点D．
(1)、请在图中画出CD在灯泡B照射下的影子DF；（保留画图痕迹，不写画法）(2)、若AE⊥BF，且DE=9米，DF=4米，请你求出这棵树的高度CD．