备考2024年中考数学计算能力训练1 有理数的运算

试卷更新日期：2024-03-25 类型：二轮复习

进入出卷网下载

一、选择题

1. 下列说法正确的是（）

A、 $- 4$ 是16的一个平方根 B、两个无理数的和一定是无理数 C、无限小数是无理数 D、0没有算术平方根

查看试题解析
2. 现规定一种运算： $a * b = a b - a - b$ ，其中 $a ， b$ 为有理数，则 $2 * (- 1) =$ （）

A、 $- 6$ B、 $- 3$ C、5 D、11

查看试题解析
3. 小夕学习了有理数运算法则后，编了一个计算程序．当他输入任意一个有理数时，显示屏上出现的结果总等于所输入的有理数的3倍与-2的差．当他第一次输入-6，然后又将所得的结果再次输入后，显示屏上出现的结果应是（　　）

A、-46 B、-50 C、-58 D、-66

查看试题解析
4. 在数学课上，老师让甲、乙、丙、丁，四位同学分别做了一道有理数运算题，你认为做对的同学是（）
甲： $9 - 3^{2} \div 8 = 0 \div 8 = 0$ ．
乙： $24 - (4 \times 3^{2}) = 24 - 4 \times 6 = 0$ ．
丙： $(36 - 12) \div \frac{3}{2} = 36 \times \frac{2}{3} - 12 \times \frac{2}{3} = 16$ ．
丁： $(- 3)^{2} \div \frac{1}{3} \times 3 = 9 \div 1 = 9$ ．

A、甲 B、乙 C、丙 D、丁

查看试题解析
5. 下列说法正确的是（）

A、有理数与数轴上的点一一对应 B、若a，b互为相反数，则 $\frac{a}{b} = - 1$ C、 $\sqrt{16}$ 的算术平方根为4 D、3.40万是精确到百位的近似数

查看试题解析
6. 定义一种关于整数n的“F”运算：
⑴当n是奇数时，结果为3n+5；
⑵当n是偶数时，结果是 $\frac{k}{2^{n}}$ （其中k是使 $\frac{k}{2^{n}}$ 是奇数的正整数），并且运算重复进行．
例如：取n＝58，第一次经F运算是29，第二次经F运算是92，第三次经F运算是23，第四次经F运算是74…；若n＝9，则第2023次运算结果是（　　）

A、6 B、7 C、8 D、9

查看试题解析
7. 对于若干个数，先将每两个数作差，再将这些差的绝对值相加，这样的运算称为对这若干个数进行“绝对运算” $.$ 例如，对于 $1$ ， $2$ ， $3$ 进行“绝对运算”，得到： $| 1 - 2 | + | 2 - 3 | + | 1 - 3 | = 4$ ．
$①$ 对 $1$ ， $3$ ， $5$ ， $10$ 进行“绝对运算”的结果是 $29$ ；
$②$ 对 $x$ ， $- 2$ ， $5$ 进行“绝对运算”的结果为 $A$ ，则 $A$ 的最小值是 $7$ ；
$③$ 对 $a$ ， $b$ ， $b$ ， $c$ 进行“绝对运算”，化简的结果可能存在 $8$ 种不同的表达式；
以上说法中正确的个数为（）

A、 $0$ B、 $1$ C、 $2$ D、 $3$

查看试题解析
8. 如图所示，数轴上 $A ， B$ 两点分别对应有理数 $a ， b$ ，则下列结论正确的是（）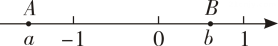

A、 $b - a < 0$ B、 $a - b > 0$ C、 $a + b > 0$ D、 $| a | - | b | > 0$

查看试题解析
9. 用“☆”定义一种新运算：对于任意有理数x和y，x☆y= $a^{2} x + a y + 1$ （a为常数），如：2☆3= $a^{2} \cdot 2 + a \cdot 3 + 1 = 2 a^{2} + 3 a + 1$ .若1☆2=3，则3☆6的值为（）

A、7 B、8 C、9 D、13

查看试题解析
10. 已知有理数 $a ， b ， c$ 满足 $a b c < 0$ ，则 $\frac{a}{| a |} + \frac{| b |}{b} + \frac{c}{| c |} - \frac{| a b c |}{a b c}$ 的值是（）

A、 $\pm 1$ B、0或2 C、 $\pm 2$ D、 $\pm 1$ 或 $\pm 2$

查看试题解析

二、填空题

11. 定义一种新运算“⊕”，规定有理数 $a \oplus b = 4 a b - b$ ，如： $2 \oplus 3 = 4 \times 2 \times 3 - 3 = 21$ ，根据该运算计算 $3 \oplus (- 3) =$ ．

查看试题解析
12. 定义新运算：对于任意有理数a，b，都有 $a \oplus b = \frac{1}{2} (| a - b | + a + b)$ ，例如 $4 \oplus 2 = \frac{1}{2} (| 4 - 2 | + 4 + 2) = 4$ .将 $1 ， 2 ， 3 ， 4 ， ⋯ ， 50$ 这50个自然数分成25组，每组2个数，进行 $a \oplus b$ 运算，得到25个结果，则这25个结果的和的最大值是.

查看试题解析
13. 对于任意有理数a，b，定义新运算：a⊗b=a²-2b+1，则2⊗（-6）= ．

查看试题解析
14. a为有理数，定义运算符号 $\nabla$ ：当 $a > - 2$ 时， $\nabla a = - a$ ；当 $a < - 2$ 时， $\nabla a = a$ ；当 $a = - 2$ 时， $\nabla a = a$ 根据这种运算，则 $\nabla [4 + \nabla (2 - 5)]$ 的值为．

查看试题解析
15. 在学习了有理数的运算后，小明定义了新的运算：取大运算“V”和取小运算“Λ”，比如：3 V 2=3，3Λ2=2，利用“加、减、乘、除”以及新运算法则进行运算，下列运算中正确的是．
①[3V（-2）]Λ4=4

②（aVb）Vc=aV（bVc）

③-（aVb）=（-a）Λ（-b）

④（aΛb）×c=acΛbc

查看试题解析
16. 已知 $a$ 、 $b$ 、 $c$ 为非零有理数，请你探究以下问题：

(1)、当 $a < 0$ 时， $\frac{a}{| a |} =$ ；

(2)、 $\frac{a b}{| a b |} + \frac{| b c |}{b c} + \frac{c a}{| c a |} + \frac{| a b c |}{a b c}$ 的最小值为．

查看试题解析
17. 设有理数a，b，c满足a+b+c=0，abc> 0，则a，b，c中正数的个数为

查看试题解析

三、计算题

18. 已知 $a$ ， $b$ 是有理数，运算“ $\oplus$ ”的定义是： $a \oplus b = a b + a - b$ .

(1)、求 $2 \oplus (- 3)$ 的值；

(2)、若 $x \oplus \frac{3}{4} = 1$ ，求 $x$ 的值；

(3)、运算“ $\oplus$ ”是否满足交换律，请证明你的结论.

查看试题解析
19. 学习了有理数的运算后，王老师给同学们出了这样的一道题．
计算： $71 \frac{15}{16} \times (- 8)$ ．
解： $= (72 - \frac{1}{16}) \times (- 8) = 72 \times (- 8) - \frac{1}{16} \times (- 8) = - 576 + \frac{1}{2} = - 575 \frac{1}{2}$ ．
请你灵活运用王老师讲的解题方法计算： $39 \frac{23}{26} \div (- \frac{1}{13})$ ．

查看试题解析
20. 用“ $Δ$ ”定义新运算，对于任意有理数a ， b ，都有 $a Δ b = a^{2} - a b$ ．例如： $7 Δ 4 = 7^{2} - 7 \times 4 = 21$ ．

(1)、求 $(- 2) Δ 5$ 的值；

(2)、若继续用“*”定义另一种新运算 $a * b = 3 a b - b^{2}$ ，例如： $1 * 2 = 3 \times 1 \times 2 - 2^{2} = 2$ ．求 $4 * (2 Δ 3)$ ．

查看试题解析
21. 现定义一种新运算“*”，对任意有理数a、b ，规定 a*b＝ab+a﹣b ，例如：1*2＝1×2+1﹣2．

(1)、求 2*（﹣3）的值；

(2)、求（﹣3）*[（﹣2）*5]的值．

查看试题解析
22. 已知a、b为有理数，现规定一种新运算※，满足 $a ※ b = a \times b + 1$ ，例如： $4 ※ 5 = 4 \times 5 + 1 = 21$ .

(1)、求 $2 ※ (- 4)$ 的值；

(2)、若 $a = 5$ ， $| b | = 3$ ，且 $a \times b < 0$ ，求 $(a ※ b) ※ (- b)$ 的值.

查看试题解析
23. 实数运算：

(1)、 $\sqrt{16} + 2 \times \sqrt{9}$ $- \sqrt[3]{27}$ ；

(2)、 $| 1 - \sqrt{2} | +$ $\sqrt{4} - \sqrt[3]{- 8}$ .

查看试题解析
24. 简便运算：

(1)、 $8^{2022} \times (- 0.125)^{2023}$ ；

(2)、 $9 9^{2} - 98 \times 100$ ．

查看试题解析
25. 定义新运算：对于任意实数a，b（a≠0）都有a*b= $\frac{b}{a}$ ﹣a+b，等式右边是通常的加、减、除运算，比如：2*1= $\frac{1}{2}$ ﹣2+1=﹣ $\frac{1}{2}$ ．

(1)、求4*5的值；

(2)、若x*（x+2）=5，求x的值．

查看试题解析
26. a、b为有理数，且 $| a + b | = a - b$ ，试求ab的值．

查看试题解析
27. 如果有理数a，b满足 $| a b - 2 | + {(1 - b)}^{2} = 0$ ，试求 $\frac{1}{a b} + \frac{1}{(a + 1) (b + 1)} + \frac{1}{(a + 2) (b + 2)} + \cdot \cdot \cdot + \frac{1}{(a + 2007) (b + 2007)}$ 的值。

查看试题解析

四、解答题

28. 如图是一个有理数混合运算的程序流程图，请根据这个流程图回答问题：
当输入的x为-16时，最后输出的结果y是多少？

查看试题解析
29. 小明对有理数 $m$ ， $n$ 定义了一种新的运算，叫做“反加法”，记作“ $m \otimes n$ ”.他写出了一些按照“反加法”运算的算式：
$(+ 3) \otimes (+ 2) = + 1$ ， $(+ 11) \otimes (- 3) = - 8$ ， $(- 2) \otimes (+ 5) = - 3$ ， $(- 6) \otimes (- 1) = + 5$ ，
$(+ \frac{1}{3}) \otimes (+ 1) = + \frac{2}{3}$ ， $(- 4) \otimes (+ 0.5) = - 3.5$ ， $(- 8) \otimes (- 8) = 0$ ， $(+ 2.4) \otimes (- 2.4) = 0$ ，
$(+ 23) \otimes 0 = + 23$ ， $0 \otimes (- \frac{7}{4}) = + \frac{7}{4}$ .
小亮看了这些算式后说：“我明白你定义的‘反加法’法则了.”他将法则整理出来给小明看，小明说：“你的理解完全正确.”

(1)、请将下面小亮整理的“反加法”法则补充完整：
①绝对值不相等的两数相“反加”，同号得，异号得，并；
②绝对值相等的两数相“反加”，都得；
③任何数与0相“反加”，都得这个数的.

(2)、若括号的作用与它在有理数运算中的作用相同，用“反加法”计算：
$[(+ 3) \otimes (- 2)] \otimes [(- 9) \otimes 0]$ .

查看试题解析
30. 已知有理数 $a$ ， b，c在数轴上的位置如图所示，

(1)、用＜，＞，＝填空： $a$ +c0，c−b0，b+ $a$ 0， $a$ bc0；

(2)、化简：| $a$ +c|+|c−b|−|b+ $a$ |．

(3)、已知2≤x≤6，求：|2-x|+|x-6|的值.

查看试题解析
31. 将一串有理数按下列规律排列，回答下列问题．

(1)、在A处的数是正数还是负数？

(2)、负数排在A、B、C、D中的什么位置？

(3)、第2015个数是正数还是负数？排在对应于A、B、C、D中的什么位置？

查看试题解析

五、实践探究题

32. 【问题情境】数学活动课上，老师让同学们探究“有理数的加减法问题”.
我们规定一种新的运算法则： $[\begin{array}{l} a & c \\ b & d \end{array}] = a + b - c - d$ ， $(\begin{array}{l} a & c \\ b & d \end{array}) = a - b + c - d$ ，其中每个运算法则的右边都是我们学过的有理数的加减法.

(1)、【问题解决】求 $[\begin{array}{l} 1 & - 3 \\ - 2 & 4 \end{array}] + (\begin{array}{l} 1 & - 3 \\ - 2 & 4 \end{array})$ 的值.

(2)、【问题探究】已知 $a = [\begin{array}{l} \frac{1}{3} & - \frac{1}{2} \\ - \frac{5}{6} & \frac{2}{3} \end{array}]$ ， $b = (\begin{array}{l} - 12 & - 8 \\ - \frac{6}{5} & \frac{7}{10} \end{array})$ ，你能比较 $a$ 和 $b$ 的大小吗？请写出比较过程.

(3)、【拓展探究】小明同学做老师布置的作业题：计算 $[\begin{array}{l} \frac{1}{2} & \otimes \\ - \frac{2}{3} & \frac{1}{2} \end{array}] - (\begin{array}{l} 4.5 & - 1.1 \\ - 3.5 & 5.6 \end{array})$ ，其中“ $\otimes$ ”是被墨水污染看不清的一个数，他知道老师给出的该题的结果是 $\frac{1}{3}$ ，请问“ $\otimes$ ”表示的数是多少？

查看试题解析