2023-2024学年初中数学湘教版七年级下学期 第4章 相交线与平行线 单元测试 B卷
试卷更新日期：2024-03-25 类型：单元试卷
一、选择题
-
1. 如图，过直线外一点画已知直线的平行线的方法，其依据是（ ）
A、同旁内角互补，两直线平行 B、两直线平行，同位角相等 C、同位角相等，两直线平行 D、内错角相等，两直线平行2.下列所示的四个图形中，∠1和∠2是同位角的是（ ）
A、②③ B、①②③ C、①②④ D、①④3. 如图，直线DE与BC相交于点O ， 与互余， ， 则的度数是（ ）
A、35° B、45° C、55° D、65°4. 已知直线 ， 将一块含角的直角三角板按如图所示的方式放置，并且顶点 ， 分别落在直线 ， 上，若 ， 则的度数是
A、 B、 C、 D、5. 如图，已知O是直线AB上一点，∠1＝40°，OD平分∠BOC ， 则∠2＝（ ）
A、70° B、60° C、55° D、45°6. 光线在不同介质中的传播速度是不同的，因此当光线从水中射向空气时，要发生折射，由于折射率相同，所以在水中平行的光线，在空气中也是平行的．如图，的度数为（ ）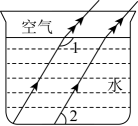
A、 B、 C、 D、7. 我市为了方便市民绿色出行，推出了共享单车服务．图①是某品牌共享单车放在水平地面的实物图，图②是其示意图，其中AB，CD都与地面l平行，∠BCD＝60°，∠BAC＝50°，当∠MAC为（ ）度时，AM∥BE．
A、15 B、65 C、70 D、1158. 如图，AB∥CD，将一副直角三角尺按如图摆放，∠GEF=60°，∠MNP=45°。有下列结论：①GE∥MP；②∠EFN=150°；③∠BEF=75°；④∠AEG=∠PMN。其中正确的个数是（ ）
A、1 B、2 C、3 D、49. 如图，AB CD，∠ABE＝ ∠EBF，∠DCE＝ ∠ECF，设∠ABE＝α，∠E＝β，∠F＝γ，则α，β，γ的数量关系是（ ）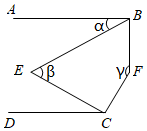
A、4β﹣α+γ＝360° B、3β﹣α+γ＝360° C、4β﹣α﹣γ＝360° D、3β﹣2α﹣γ＝360°10. 如图，ABCD，PG平分∠EPF，∠A+∠AHP＝180°，下列结论：①CDPH；②∠BEP+∠DFP＝2∠EPG；③∠FPH＝∠GPH；④∠A+∠AGP+∠DFP-∠FPG＝180°；其中正确结论是（ ）
A、①②③④ B、①②④ C、①③④ D、①②二、填空题
-
11. 一副三角尺按如图所示叠放在一起，其中点 B，D重合，若固定三角形 AOB，改变三角尺ACD的位置（其中 A 点位置始终不变），当∠BAD= 时，CD∥AB。
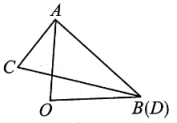12. 如图，已知直线a⊥c，b⊥c.若∠1=110°，则∠2 的度数为°.
13. 如图，一块白色正方形台布，边长为1.8m，上面横、竖各有两道等宽的黑条，黑条的宽度为0.2m，则白色部分的面积为m².
14. 如图，已知AB∥DE，∠ABC=70°，∠CDE=140°，则∠BCD的度数为.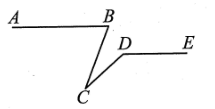
15. 如图，已知AB∥CD，BE、DE分别平分∠ABF、∠CDF，∠F＝40°，则∠E＝ ．
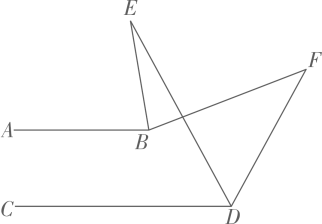16. 为保证安全，某两段铁路两旁安置了两座可旋转探照灯A，B，探照灯的光线可看作射线如图，灯A的光线从射线开始，绕点A顺时针旋转至射线上便立即回转，灯B光线从射线开始，绕点B顺时针旋转至射线便立即回转，两灯不停交叉照射巡视．已知 ， 连接 ， ， 则；若灯B的光线先转动，每秒转动 ， 45秒后灯A的光线才开始转动，每秒转动 ， 在灯B的光线第一次到达之前，灯A的光线转动秒时，两灯的光线互相平行．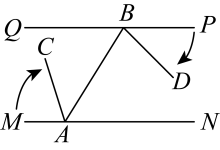
三、作图题
-
17. 如图，表示一条弯曲的小河，表示一条笔直的公路，点 ， 表示两个村庄.
(1)、在小河哪处架桥可以使村和村之间的路程最短？作出图形 ， 并将桥的位置记为点；(2)、为了方便村村民出行，现计划在公路边新建一个公交站点，使得村到该公交站点的距离最短，作出图形 ， 并将公交站点的位置记为点.四、解答题
-
18. 如图，BD是∠ABC的平分线，∠ABE+∠BCF=180°。
(1)、若∠ABC=70°，求∠BCF的值.(2)、试说明：DE∥CF.(3)、若CB是∠ACF 的平分线，∠ADB=k∠ABD，求k的值。19. 如图，已知∠EFC+∠BDC=180°，∠DEF=∠B.
(1)、试判断DE与BC的位置关系，并说明理由.(2)、若DE平分∠ADC，∠BDC=3∠B，求∠EFC的度数.20. 如图，已知点 A 在EF 上，点 P，Q在 BC上，∠E=∠EMA，∠BQM=∠BMQ
(1)、试说明：EF∥BC.(2)、若 FP⊥AC，∠2+∠C=90°，试说明：∠1=∠B.(3)、若∠3+∠4=180°，∠BAF=3∠F-20°，求∠B 的度数.五、实践探究题
-
21.
(1)、【猜想】如图 ， ， 点在直线、之间，连结、若 ， ， 则的大小为 度
(2)、【探究】如图 ， 、、交于点 ， 探究、、之间的数量关系．
(3)、【拓展】如图 ， ， 、分别平分和 ， 且、所在直线交于点 ， 过点作 ， 若 ， 则 度22. 如图 ， 某校七年级数学学习小组在课后综合实践活动中，把一个直角三角尺的直角顶点放在互相垂直的两条直线、的垂足处，并使两条直角边落在直线、上，将绕着点顺时针旋转 ．
(1)、如图 ， 若 ， 则 ， ；(2)、若射线是的角平分线，且 ．若旋转到图的位置，的度数为多少？用含的代数式表示
在旋转过程中，若 ， 求此时的值．
六、综合题
-
23. 如图1，大课间的广播操展让我们充分体会到了一种整体的图形之美，洋洋和乐乐想从数学角度分析下如何能让班级同学们的广播操做得更好，他们搜集了标准广播操图片进行讨论，如图2，为了方便研究，定义两手手心位置分别为A ， B两点，两脚脚跟位置分别为C ， D两点，定义A ， B ， C ， D平面内O为定点，将手脚运动看作绕点O进行旋转：
(1)、填空：如图2，A ， O ， B三点共线，且∠AOC＝∠BOC ， 则∠AOC＝°；(2)、第三节腿部运动中，如图3，洋洋发现，虽然A ， O ， B三点共线，却不在水平方向上，且∠AOD：∠BOC＝3：2．他经过计算发现，∠AOC﹣∠BOD的值为定值，请判断洋洋的发现是否正确，如果正确请求出这个定值，如果不正确，请说明理由；(3)、第四节体侧运动中，乐乐发现，两腿左右等距张开且∠COD＝30°，开始运动前A、O、B三点在同一水平线上，OA、OB绕点O顺时针旋转，OA旋转速度为50°/s ， OB旋转速度为25°/s ， 当OB旋转到与OD重合时，运动停止，如图4．①运动停止时，直接写出∠AOD＝ ▲ ；
②请帮助乐乐求解运动过程中∠AOC与∠BOE的数量关系．
24. 已知直线 ， ， 分别是直线 ， 上的一点，为平面上一点，为延长线上的一点，交于点F ， 和的角平分线 ， 相交于点 ．
(1)、如图1，①若 ， ， 求的度数．
②试说明： ．
(2)、如图2，当点N位于点F的左侧时，若试求的度数．
-