2023-2024学年初中数学湘教版七年级下学期 第4章 相交线与平行线 单元测试 A卷
试卷更新日期:2024-03-25 类型:单元试卷
一、选择题
-
1. 下列4个图案中,能通过平移其中一部分而得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,下列说法错误的是( )
2. 如图,下列说法错误的是( )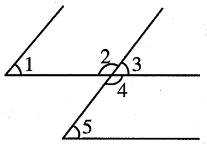
①∠1和∠3 是同位角;②∠1和∠5是同位角;③∠1和∠2 是同旁内角;④∠1和∠4是内错角。
A、①② B、②③ C、②④ D、③④3. 如图,直线a,b被直线c 所截,则∠1的同位角是 ( )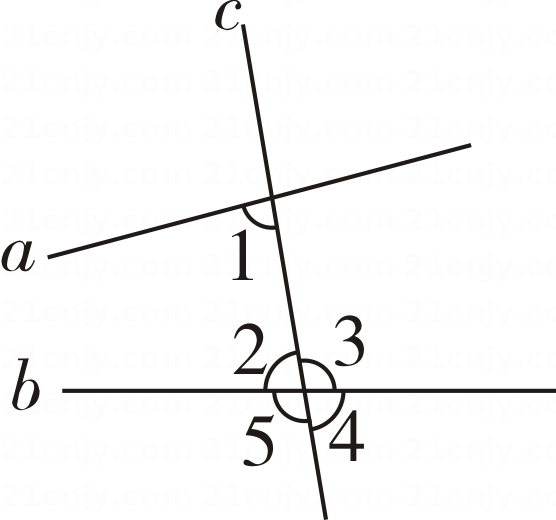 A、∠2 B、∠3 C、∠4 D、∠54. 如图,直线a∥b,∠1=55°,则∠2的度数为 ( )
A、∠2 B、∠3 C、∠4 D、∠54. 如图,直线a∥b,∠1=55°,则∠2的度数为 ( )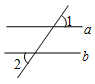 A、35° B、45° C、55° D、125°5. 在下列四边形中,AB不平行于 CD的是( )A、
A、35° B、45° C、55° D、125°5. 在下列四边形中,AB不平行于 CD的是( )A、 B、
B、 C、
C、 D、
D、 6. 在同一平面内,对两条直线可能的位置关系,描述最准确的是 ( )A、平行 B、相交 C、平行或相交 D、平行、相交或垂直7. 已知直线AB和直线AB 外一点 P,过点 P作直线与AB 平行,这样的直线 ( )A、有且只有一条 B、不止一条 C、不存在 D、不存在或只有一条8. 如图,下列条件中,能判定 AD∥BE 的是( )
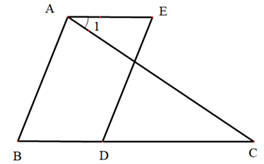
6. 在同一平面内,对两条直线可能的位置关系,描述最准确的是 ( )A、平行 B、相交 C、平行或相交 D、平行、相交或垂直7. 已知直线AB和直线AB 外一点 P,过点 P作直线与AB 平行,这样的直线 ( )A、有且只有一条 B、不止一条 C、不存在 D、不存在或只有一条8. 如图,下列条件中,能判定 AD∥BE 的是( ) A、∠1=∠2 B、∠3=∠4 C、∠B+∠ADC=180° D、∠B=∠DCE9. 如图,把一块含有30°角的三角尺的两个顶点放在直尺的对边上,如果∠1=22°,那么∠2的度数是( )
A、∠1=∠2 B、∠3=∠4 C、∠B+∠ADC=180° D、∠B=∠DCE9. 如图,把一块含有30°角的三角尺的两个顶点放在直尺的对边上,如果∠1=22°,那么∠2的度数是( ) A、22° B、32° C、38° D、44°10. 如图,将周长为8 的△ABC沿BC 方向平移2个单位长度得到△DEF,则四边形 ABFD的周长为( )
A、22° B、32° C、38° D、44°10. 如图,将周长为8 的△ABC沿BC 方向平移2个单位长度得到△DEF,则四边形 ABFD的周长为( ) A、10 B、12 C、14 D、16
A、10 B、12 C、14 D、16二、填空题
-
11. 若∠α与∠β的两边分别平行,且∠α=(2x+10)°,∠β=(3x-20)°,则∠α的度数为。12. 如图,把 块三角板 ABC的直角顶点B放在直线EF 上,∠C=30°,AC∥EF,则∠1 的度数为°.
 13. 如图,直线l1∥l2 , ∠1=20°,则∠2+∠3=°.
13. 如图,直线l1∥l2 , ∠1=20°,则∠2+∠3=°.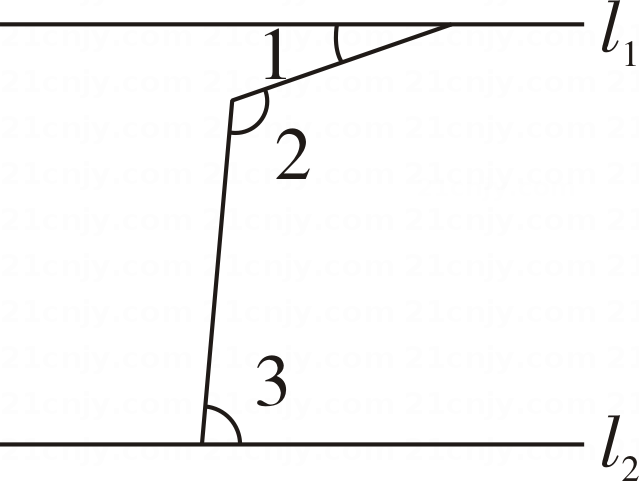 14. 如图,已知∠1=80°,∠2=100°,∠3=70°,则∠4=.
14. 如图,已知∠1=80°,∠2=100°,∠3=70°,则∠4=. 15. 如图,将三角形 ABC 向左平移3cm得到三角形 DEF,AB,DF 相交于点G.如果三角形 ABC 的周长是12cm,那么三角形ADG与三角形BGF 的周长之和是cm.
15. 如图,将三角形 ABC 向左平移3cm得到三角形 DEF,AB,DF 相交于点G.如果三角形 ABC 的周长是12cm,那么三角形ADG与三角形BGF 的周长之和是cm.
三、作图题
-
16. 如图,将三角形ABC平移得到三角形DEF,且F为点C的对应点,请画出平移后的三角形DEF.
 17. 如图,在四边形中, , .
17. 如图,在四边形中, , . (1)、用直尺和圆规作的角平分线 , 交于点保留作图痕迹,不写作法;(2)、求的度数补全下列推理过程 .
(1)、用直尺和圆规作的角平分线 , 交于点保留作图痕迹,不写作法;(2)、求的度数补全下列推理过程 .解:已知
( )
已知
平分已知
▲ 角平分线的定义
已知
▲ °( )
四、解答题
-
18. 如图,AB∥CD,EF分别交AB,CD于点M,N,∠1=52°,MG平分∠BMF交CD于点G,求∠2的度数.
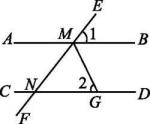 19. 如图,已知AB∥CD , ∠A=∠C , 那么CE∥AD成立吗?为什么?
19. 如图,已知AB∥CD , ∠A=∠C , 那么CE∥AD成立吗?为什么?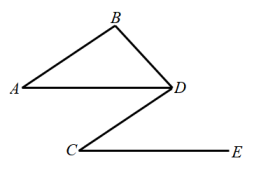 20. 已知:如图,△ABC中,点D,E分别在AB,AC上,EF交DC于点F,∠3+∠2=180°,∠1=∠B.
20. 已知:如图,△ABC中,点D,E分别在AB,AC上,EF交DC于点F,∠3+∠2=180°,∠1=∠B. (1)、试说明:DE∥BC.(2)、若DE平分∠ADC,∠3=3∠B,求∠2的度数。
(1)、试说明:DE∥BC.(2)、若DE平分∠ADC,∠3=3∠B,求∠2的度数。五、实践探究题
-
21. 【问题背景】
如图,已知直线 , 点为直线 , 之间的一个动点,连接 , , 平分 , 平分 , 和交于点 .
(1)、【问题提出】如图1,求证:;
 (2)、【拓展延伸】
(2)、【拓展延伸】如图2,连接 , 在点运动过程中,当满足 , 时:
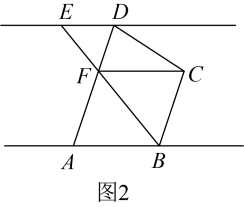
①若 , 求度数;
②若 , 求度数.
22. 问题背景:如图①:将一副三角板中的两个直角顶点叠放在一起,其中 , , .

问题提出:
(1)、将这两个三角板按如图①放置,若 , 则;(2)、将这两个三角板按如图②放置,当时,求的度数;操作探究:
(3)、若保持两个三角板的直角顶点叠放在一起,三角板保持不动,试探究三角板如何放置时, , 此时等于多少度?请画出草图,并说明理由六、综合题