2023-2024学年初中数学湘教版七年级下学期第2章整式的乘法单元测试 B卷

试卷更新日期：2024-03-25 类型：单元试卷

进入出卷网下载

一、选择题

1. 下列运算正确的是（）

A、 $x^{2} + x^{2} = x^{4}$ B、 $3 a^{3} \cdot 2 a^{2} = 6 a^{6}$ C、 $2 x^{4} \cdot (- 3 x^{4}) = 6 x^{8}$ D、 ${(- a^{2})}^{3} = - a^{6}$

查看试题解析
2. 计算： ${(a^{2})}^{3} \cdot a^{5} =$ （）

A、 $a^{10}$ B、 $a^{11}$ C、 $a^{13}$ D、 $3 a^{7}$

查看试题解析
3. 如图，用不同的代数式表示图中阴影部分的面积，可得等式（）

A、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ B、 ${(a - b)}^{2} = a^{2} + 2 a b - b^{2}$ C、 $(a + b) (a - b) = a^{2} - b^{2}$ D、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

查看试题解析
4. 已知： $(2 x + 1) (x - 3) = 2 x^{2} + px + q$ ，则p，q的值分别为（）

A、5，3 B、5，−3 C、−5，3 D、−5， −3

查看试题解析
5. 对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式．例如，利用图1可以得到 $a (a + b) = a^{2} + a b$ ，那么利用图2所得到的数学等式为（）

A、 ${(a + b + c)}^{2} = a^{2} + b^{2} + c^{2}$ B、 ${(a + b + c)}^{2} = 2 a^{2} + 2 b^{2} + 2 c^{2}$ C、 ${(a + b + c)}^{2} = a^{2} + b^{2} + c^{2} + a b + b c + c a$ D、 ${(a + b + c)}^{2} = a^{2} + b^{2} + c^{2} + 2 a b + 2 b c + 2 c a$

查看试题解析
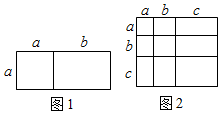6. 若一个正整数能表示为两个连续奇数的平方差，则称这个正整数为“好数”．下列正整数中能称为“好数”的是（　　）

A、205 B、250 C、502 D、520

查看试题解析
7. 如果一个正整数可以表示为两个连续奇数的平方差，那么称该正整数为“和谐数”（如 $8 = 3^{2} - 1^{2}$ ， $16 = 5^{2} - 3^{2}$ ，则8，16均为“和谐数”），在不超过80的正整数中，所有的“和谐数”之和为（）

A、430 B、440 C、450 D、460

查看试题解析
8. 式子 $(2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) \cdot \cdot \cdot (2^{1010} + 1)$ 化简的结果为（）

A、 $2^{1010} - 1$ B、 $2^{1010} + 1$ C、 $2^{2020} - 1$ D、 $2^{2020} + 1$

查看试题解析
9. 已知2ⁿ＋2¹²＋1（n＜0）是一个有理数的平方，则n的值为（）

A、﹣16 B、﹣14 C、﹣12 D、﹣10

查看试题解析
10. 如图有两张正方形纸片A和B ，图1将B放置在A内部，测得阴影部分面积为2，图2将正方形AB并列放置后构造新正方形，测得阴影部分面积为20，若将3个正方形A和2个正方形B并列放置后构造新正方形如图3，（图2，图3中正方形AB纸片均无重叠部分）则图3阴影部分面积（）

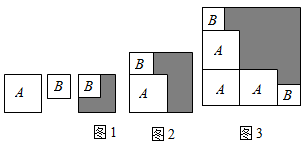A、22 B、24 C、42 D、44

查看试题解析

二、填空题

11. 计算： $(2 x + y) (2 x - y) =$ ．

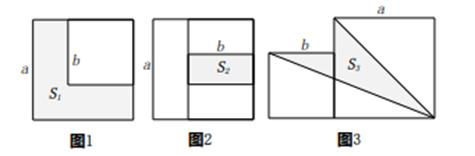
查看试题解析
12. 已知a+b=7，ab=2，则a²+b²= ．

查看试题解析
13. 若4x²+kx+25是一个完全平方式，则k的值是．

查看试题解析
14. 一个多项式与 $(x - 1) (x + 1)$ 的积为 $x^{3} - m x^{2} + n x + 2$ ，则 $m + 2 n =$ .

查看试题解析
15. 两个边长分别为a和b的正方形如图放置（图1），其未叠合部分（阴影）面积为S₁；若再在图1中大正方形的右下角摆放一个边长为b的小正方形（如图2），两个小正方形叠合部分（阴影）面积为S₂ ．若a+b＝8，ab＝10，则S₁+S₂=；当S₁+S₂＝40时，则图3中阴影部分的面积S₃=.

查看试题解析

三、计算题

16. 计算：

(1)、(2x-3y-1)(2x+3y-1)

(2)、(2a+b)²(2a-b)²

查看试题解析
17. 用简便方法计算：

(1)、 $99^{2} + 198 + 1 .$

(2)、198²-396×202+202².

查看试题解析

四、解答题

18. 现有长为a ，宽为b的长方形卡片（如图①）若干张，某同学用4张卡片拼出了一个大正方形（不重叠、无缝隙，如图②）．

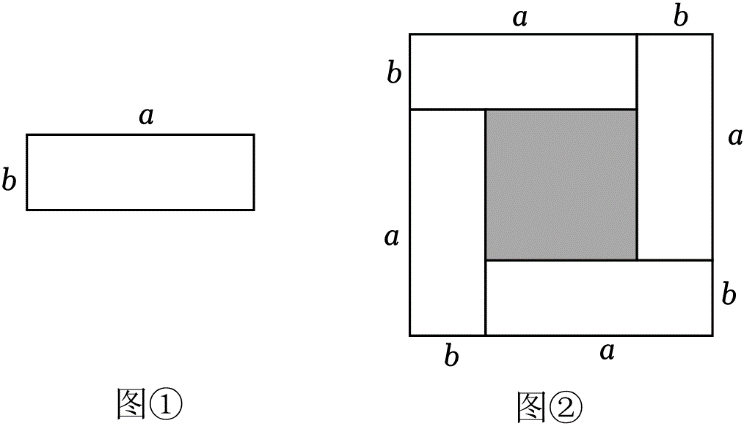(1)、图②中，大正方形的边长是，阴影部分正方形的边长是．（用含a ， b的式子表示）

(2)、用两种方法表示图②中阴影部分正方形的面积（不化简），并用一个等式表示（a+b）² ，（a﹣b）² ， ab三者之间的数量关系．

(3)、已知a+b＝8，ab＝7，求图②中阴影部分正方形的边长．

查看试题解析
19. 为创建文明校园环境，高校长制作了“节约用水”“讲文明，讲卫生”等宣传标语，标语由如图 $①$ 所示的板材裁剪而成，其为一个长为 $2 m$ ，宽为 $2 n$ 的长方形板材，将长方形板材沿图中虚线剪成四个形状和大小完全相同的小长方形标语，在粘贴过程中，同学们发现标语可以拼成图 $②$ 所示的一个大正方形．

(1)、用两种不同方法表示图 $②$ 中小正方形 $($ 阴影部分 $)$ 面积：
方法一： $S_{小正方形} =$ ；
方法二： $S_{小正方形} =$ ；

(2)、 $(m + n)^{2}$ ， $(m - n)^{2}$ ， $4 m n$ 这三个代数式之间的等量关系为；

(3)、根据 $(2)$ 题中的等量关系，解决如下问题：
$①$ 已知： $a - b = 5$ ， $a b = - 6$ ，求： $(a + b)^{2}$ 的值；
$②$ 已知： $a - \frac{1}{a} = 1$ ，求： $(a + \frac{1}{a})^{2}$ 的值．

查看试题解析

五、实践探究题

20. 探究应用：

(1)、计算： $(a - 1) (a^{2} + a + 1) = a^{3} + a^{2} + a - a^{2} - a - 1 = a^{3} - 1$ ；
$(2 x - y) (4 x^{2} + 2 x y + y^{2}) =$ =；

(2)、（1）中的整式乘法计算结果很简洁，由（1）发现一个新的乘法公式：
（a—b）（）=（）（用含a、b的字母表示）；

(3)、下列各项能用（2）中你发现的乘法公式计算的是（）

A、 $(a - 3) (a^{2} - 3 a + 9)$ B、 $(2 m - n) (2 m^{2} + 2 m n + n^{2})$ C、 $(4 - x) (16 + 4 x + x^{2})$ D、 $(m - n) (m^{2} + 2 m n + n^{2})$

(4)、求 $(3 x - 2 y) (9 x^{2} + 6 x y + 4 y^{2})$ 的值.

查看试题解析
21. 对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式，例如图1，可以得到数学等式： $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ 。请解答下列问题：

(1)、写出图2中所表示的数学等式：。

(2)、利用（1）中得到的结论，解决下面的问题：若a+b+c=10，ab+ac+bc=35，则 $a^{2} + b^{2} + c^{2} =$ 。

(3)、小明同学用图3中x张边长为a的正方形，y张边长为b的正方形，z张边长分别为a，b的长方形纸片拼出一个面积为（3a+2b）（2a+b）的长方形，请参照上述拼接的方法，求x+y+z的值。

查看试题解析
22. 阅读材料：
类比是常用的数学思想.比如，我们可以类比多位数的竖式运算方法，得到多项式与多项式的运算方法.
① $\frac{1}{2 x + 3} \frac{+ ） 3 x - 5}{5 x - 2}$
∴（2x+3）+（3x-5）=5x-2. $② 3 x^{2} - 4 x + 1$
$\frac{- ） x^{2} + 0 - 5}{2 x^{2} - 4 x + 6}$
$∴ (3 x^{2} - 4 x + 1) - (x^{2} - 5) = 2 x^{2} - 4 x + 6 ，$ ③x+3
$\frac{\times ） 2 x + 5}{5 x + 15}$
$\frac{2 x^{2} + 6 x}{2 x^{2} + 11 x + 15}$
$∴ (x + 3) (2 x + 5) = 2 x^{2} + 11 x + 15 .$
理解应用：

(1)、请仿照上面的竖式方法计算：（2x+3）（x-5）.

(2)、已知两个多项式的和为 $3 x^{2} - \frac{7}{2} x + 5 ，$ 其中一个多项式为x²-2，请用竖式的方法求出另一个多项式.

(3)、已知一个长为（x+2）、宽为（x-2）的长方形A，将它的长增加8，宽增加a得到一个新长方形B（如图），若长方形B的周长是A 的周长的3倍，求长方形 B的面积（用含x的代数式表示）.

查看试题解析

六、综合题

23. 【观察】观察下列各式，并回答下面的问题
$\frac{1}{1 \times 3} = \frac{1}{2} \times (1 - \frac{1}{3})$ ； $\frac{1}{2 \times 4} = \frac{1}{2} \times (\frac{1}{2} - \frac{1}{4})$ ； $\frac{1}{3 \times 5} = \frac{1}{2} \times (\frac{1}{3} - \frac{1}{5}) \cdot \cdot \cdot \cdot \cdot \cdot$

(1)、【猜想】第 $n$ 个等式为；

(2)、【验证】请验证以上结论；

(3)、【运用】运用以上规律解方程：
$\frac{1}{x (x + 2)} + \frac{1}{(x + 2) (x + 4)} + \frac{1}{(x + 4) (x + 6)} + \cdot \cdot \cdot \cdot \cdot \cdot + \frac{1}{(x + 48) (x + 50)} = \frac{1}{x + 50}$ ．

查看试题解析

2023-2024学年初中数学湘教版七年级下学期 第2章 整式的乘法 单元测试 B卷

一、选择题

二、填空题

三、计算题

四、解答题

五、实践探究题

六、综合题

2023-2024学年初中数学湘教版七年级下学期第2章整式的乘法单元测试 B卷