2023-2024学年初中数学湘教版七年级下学期第2章整式的乘法单元测试 A卷

试卷更新日期：2024-03-25 类型：单元试卷

进入出卷网下载

一、选择题

1. 下列运算正确的是（）

A、a³•a²＝a⁶ B、4ab-ab＝4 C、（a+1）²＝a²+1 D、（-a³）²＝a⁶

查看试题解析
2. 计算 $x \cdot x^{2}$ 的结果是（）

A、 $3 x$ B、 $x^{2}$ C、 $x$ D、 $x^{3}$

查看试题解析
3. 下列多项式的乘法中可用平方差公式计算的是（）

A、(1+x)(x+1) B、(-a+b)(a-b) C、(x²-y)(y²+x) D、 $(\frac{1}{2} a + b) (b - \frac{1}{2} a)$

查看试题解析
4. 下列计算中，不正确的是（）

A、 $(x - 2) (2 x + 3) = 2 x^{2} - x - 6$ B、 $(2 x - 1) (2 x + 1) = 4 x^{2} - 1$ C、 $(a + 2 b) (2 x - y) = 2 a x - a y + 4 b x - 2 b y$ D、 $(3 x - 2) (x + 4) = 3 x^{2} + 14 x - 8$

查看试题解析
5. 若 $(y + 3) (y - 2) = y^{2} + m y + n$ 恒成立，则m，n 的值分别为（）

A、m=5，n=6 B、m=1，n=-6 C、m=1，n=6 D、m=5，n= -6

查看试题解析
6. 计算 ${(- 1 \frac{1}{2})}^{2021} \times {(\frac{2}{3})}^{2023}$ 的结果等于（）

A、1 B、-1 C、 $- \frac{9}{4}$ D、 $- \frac{4}{9}$

查看试题解析
7. 从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后，将其截成四个相同的等腰梯形（如图甲），然后拼成一个平行四边形（如图乙），那么通过计算两个图形阴影部分的面积，可以验证成立的式子为（）

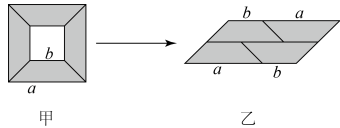A、(a+b)²=a²+2ab+b² B、(a- b)²= a²-2ab+b² C、a²- b²=(a+b) (a- b) D、(a+2b) (a+b)= a²+3ab+2b²

查看试题解析
8. 如图在边长为a的正方形纸片中剪去一个边长为b的小正方形，把余下的部分沿虚线剪开，拼成一个矩形，分别计算这两个图形阴影部分的面积，可以验证的等式是（）

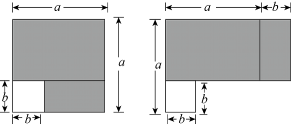A、 $a^{2} - b^{2} = (a + b) (a - b)$ B、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ C、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ D、 $a^{2} + a b = a (a + b)$

查看试题解析
9. 如图为2024年某月日历，现用一个正方形方框框住部分（阴影部分）9个位置上的数，若最小的数与最大的数的积记为n，中间位置上的数记为m．下列所给的数据中，n不可能是（）

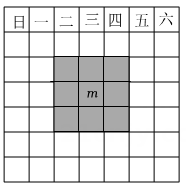A、377 B、420 C、465 D、512

查看试题解析
10. 我国宋代数学家杨辉发现了 ${(a + b)}^{n}$ （ $n = 0$ ， 1，2，3，…）展开式系数的规律：
以上系数三角表称为“杨辉三角”，根据上述规律， ${(a + b)}^{8}$ 展开式的系数和是（）

A、64 B、128 C、256 D、612

查看试题解析

二、填空题

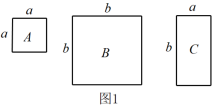
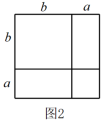
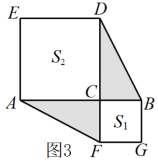
11. 计算：（﹣2x²y）³= ．

查看试题解析
12. 已知 $a^{m} = 2$ ， $a^{n} = 3$ （m，n为正整数），则 $a^{3 m + n} =$ .

查看试题解析
13. 已知 $a b = 12 ， a^{2} + b^{2} = 25 ，则 {(a + b)}^{2} =$ ．

查看试题解析
14. 下列算式①（2²×3²）³；②（2×6²）×（3×6³）；③6³+6³；④（2²）³×（3³）² 中，结果等于6⁶的有。

查看试题解析
15. 若 $25 x^{2} + 1$ 加上一个单项式能成为一个完全平方式，则这个单项式为.

查看试题解析
16. 两个相同的小长方形按如图1所示的方式摆放，重叠部分是边长为b的正方形，阴影部分的面积为S.四个相同的小长方形按如图2所示的方式摆放，左上角形成的是边长为b的正方形阴影，此阴影部分的面积为 S₁，另一阴影部分的面积为S₂，则S，S₁，S₂之间的数量关系为

查看试题解析

三、计算题

17. 计算：

(1)、 $3 a (a - 2 b + 1)$

(2)、 $(x - 2 y) (x + 2 y)$

查看试题解析
18. 计算：

(1)、 $m \cdot m^{2} \cdot (- m)^{5}$

(2)、 $a^{2} \cdot a^{4} + {(- a^{2})}^{3}$

查看试题解析

四、解答题

19. 已知a+2b=1，ab=-1．求：

(1)、a²+4b²的值。

(2)、(a-2b)²的值。

查看试题解析
20.

(1)、计算： $(a - b)^{2} + (b - c)^{2} + (c - a)^{2} .$

(2)、已知a-b=10，b-c=5，利用(1)的结论，求： $a^{2} + b^{2} + c^{2} - a b - b c - a c$ 的值.

查看试题解析
21. 按要求计算.

(1)、利用完全平方公式计算：501².

(2)、利用平方差公式计算：889²-888².

查看试题解析

五、实践探究题

22. 小明把图1中L形的纸片进行如图2所示的剪拼，变成了一个长方形，请你结合图形验证平方差公式.

查看试题解析
23. 探究应用：

(1)、计算： $(x + 1) (x^{2} - x + 1) =_{.}$
$(2 x + y) (4 x^{2} - 2 x y + y^{2}) =_{.}$

(2)、上面的乘法计算结果很简洁，你发现了什么规律(公式)?用含a，b的字母表示该公式为：.

(3)、下列各式能用上述公式计算的是____.

A、(m+2)(m²+2m+4) B、(m+2n)(m²-2mn+2n²) C、(3+n)(9-3n+n²) D、(m+n)(m²-2mn+n²)

查看试题解析
24. 公式的探究与应用：

(1)、如图1所示，可以求出阴影部分的面积是多少(写成两数平方差的形式)？

(2)、若将图1的阴影部分裁剪下来，重新拼成一个如图2所示的长方形，求此长方形的面积(写成多项式乘法的形式)．

(3)、比较两图阴影部分的面积，可以得到一个公式：.

(4)、运用公式计算：(1- $\frac{1}{2^{2}}$ )(1- $\frac{1}{3^{2}}$ )(1- $\frac{1}{4^{2}}$ )……(1- $\frac{1}{9 9^{2}}$ )(1- $\frac{1}{10 0^{2}}$ )

查看试题解析

六、综合题

25.

(1)、已知 $a + b = 5 ， a b = - \frac{1}{4} ，$ 求下列各式的值：① $a^{2} + b^{2} .$
②(a-b)².

(2)、若 $x + \frac{3}{2} y - 2 z + 1 = 0 ，$ 求 $9^{x} \cdot 27^{y} \div 81^{z}$ 的值.

查看试题解析
26. 数学课上，老师用图1中的一张边长为a的正方形纸片A，1张边长为b的正方形纸片B和2张宽与长分别为a与b的长方形纸片C，拼成了如图2所示的大正方形，观察图形并解答下列问题：

(1)、由图1和图2可以得到的等式为（用含a，b的等式表示）；

(2)、莉莉想用这三种纸片拼出一个面积为 $(2 a + b) (a + 2 b)$ 的大长方形，求需A，B，C三种纸片各多少张；

(3)、如图3，S₁ ， S₂分别表示边长为p，q的正方形的面积，且A，B，C三点在一条直线上， $S_{1} + S_{2} = 20$ ， $p + q = 6$ ．求图中阴影部分的面积．

查看试题解析

2023-2024学年初中数学湘教版七年级下学期 第2章 整式的乘法 单元测试 A卷

一、选择题

二、填空题

三、计算题

四、解答题

五、实践探究题

六、综合题

2023-2024学年初中数学湘教版七年级下学期第2章整式的乘法单元测试 A卷