湖北省2024年中考适应性模拟(元调卷三)数学试卷
试卷更新日期:2024-03-25 类型:中考模拟
一、选择题(共10小题,每小题3分,共30分)
-
1. 下列图形的各条边均相等,其中不是中心对称图形的是( )A、
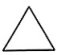 B、
B、 C、
C、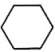 D、
D、 2. 有两个事件,事件(1):随意翻到一本书的某页,这页的页码是奇数;事件(2);通常温度降到0℃以下,纯净的水结冰.下列判断正确的是( )A、(1)(2)都是随机事件 B、(1)(2)都是必然事件 C、(1)是必然事件,(2)是随机事件 D、(1)是随机事件,(2)是必然事件3. 解一元二次方程x2-6x-1=0,配方后正确的是( )A、(x-3)2=8 B、(x-6)2=37 C、(x-3)2=10 D、(x-6)2=354. 已知一元二次方程x2-3x-15=0的两根分别为m,n,则mn-m-n的值是( )A、18 B、-12 C、-18 D、125. 如图,⊙O和直线l1 , 直线l2在同一平面内,AB是⊙O的直径,直线l2是⊙O的切线,直线l1经过点A,下列条件不能判定直线l1与⊙O相切的是( )
2. 有两个事件,事件(1):随意翻到一本书的某页,这页的页码是奇数;事件(2);通常温度降到0℃以下,纯净的水结冰.下列判断正确的是( )A、(1)(2)都是随机事件 B、(1)(2)都是必然事件 C、(1)是必然事件,(2)是随机事件 D、(1)是随机事件,(2)是必然事件3. 解一元二次方程x2-6x-1=0,配方后正确的是( )A、(x-3)2=8 B、(x-6)2=37 C、(x-3)2=10 D、(x-6)2=354. 已知一元二次方程x2-3x-15=0的两根分别为m,n,则mn-m-n的值是( )A、18 B、-12 C、-18 D、125. 如图,⊙O和直线l1 , 直线l2在同一平面内,AB是⊙O的直径,直线l2是⊙O的切线,直线l1经过点A,下列条件不能判定直线l1与⊙O相切的是( )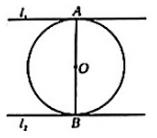 A、l1∥l2 B、l1⊥AB C、l1与⊙O只有一个公共点 D、点O到l1上某点的距离等于半径6. 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是73,设每个支干长出x个小分支,则可列方程为( )A、1+x+x2=73 B、(1+x)2=73 C、x+x2=73 D、1+(1+x)+(1+x)2=737. 如图,在平面直角坐标系中,将点P(1,3)绕点A(2,0)顺时针旋转90°后得到点P1 , 再将点P1绕点A顺时针旋转90°后得到P2 , 再将点P2绕点A顺时针旋转90°后得到P3 , 依此类推,则P2023的坐标是( )
A、l1∥l2 B、l1⊥AB C、l1与⊙O只有一个公共点 D、点O到l1上某点的距离等于半径6. 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是73,设每个支干长出x个小分支,则可列方程为( )A、1+x+x2=73 B、(1+x)2=73 C、x+x2=73 D、1+(1+x)+(1+x)2=737. 如图,在平面直角坐标系中,将点P(1,3)绕点A(2,0)顺时针旋转90°后得到点P1 , 再将点P1绕点A顺时针旋转90°后得到P2 , 再将点P2绕点A顺时针旋转90°后得到P3 , 依此类推,则P2023的坐标是( )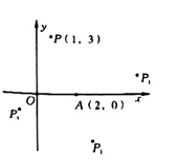 A、(5,1) B、(3,-3) C、(-1,-1) D、(1,3)8. 已知二次函数y=ax2+bx+c(a为常数,且a>0)的图象上有四点A(-1,y1),B(3,y1),C(2,y2),D(-2,y3),则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y1<y3 C、y2<y3<y1 D、y3<y1<y29. 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,∠ACB=60°, , BC=8,则△BDE的面积是( )
A、(5,1) B、(3,-3) C、(-1,-1) D、(1,3)8. 已知二次函数y=ax2+bx+c(a为常数,且a>0)的图象上有四点A(-1,y1),B(3,y1),C(2,y2),D(-2,y3),则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y1<y3 C、y2<y3<y1 D、y3<y1<y29. 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,∠ACB=60°, , BC=8,则△BDE的面积是( ) A、10 B、 C、 D、10. 类比“赵爽弦图”,可类似地构造如图所示的图形,它是由中间的小正六边形和6个全等的直角三角形拼成的一个大正六边形,若在大正六边形内部随机取一点,则此点取自小正六边形的概率是( )
A、10 B、 C、 D、10. 类比“赵爽弦图”,可类似地构造如图所示的图形,它是由中间的小正六边形和6个全等的直角三角形拼成的一个大正六边形,若在大正六边形内部随机取一点,则此点取自小正六边形的概率是( )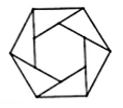 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共6小题,每小题3分,共18分)
-
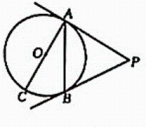
11. 在平面直角坐标系中,点P(1,-3)关于原点对称的点的坐标是12. 一个直角三角形的两条直角边的和是14,面积是24,则该直角三角形的斜边长为.13. 如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,已知∠CAB=29°,则∠P的大小是.
 14. 经过某三岔路口的汽车,可能向左转或向右转.如果这两种可能性大小相同,则三辆汽车经过这个三岔路口时,至少有2辆车向左转的概率是.15. 已知抛物线y=ax2+bx+c(a,b,c是常数,a<0)经过点(2,0),且2<c<3.下列四个结论:
14. 经过某三岔路口的汽车,可能向左转或向右转.如果这两种可能性大小相同,则三辆汽车经过这个三岔路口时,至少有2辆车向左转的概率是.15. 已知抛物线y=ax2+bx+c(a,b,c是常数,a<0)经过点(2,0),且2<c<3.下列四个结论:①方程ax2+bx+c=0有两个不相等的实数根;
②若对任意的实数m,都有bm-b≥am2-a,则
③若抛物线经过点(-1,0),在抛物线上有且仅有2个点到x轴的距离等于n(n>0),则;
④点A(x1 , y1),B(x2 , y2)在抛物线上,且都在y轴右侧,若4a+c>0,则(x1-x2)(y1-y2)>0.
其中正确的是(填写序号).
16. 如图,在四边形ACBD中,BC=5,∠ACB+∠ADB=90°,连接AB,CD,若AB=AD,△ABC的面积为 , 则CD的长为.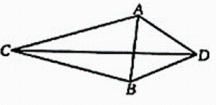
三、解答题(17-21每题8分,22-23每题10分,24题12分,共72分)
-
17. 若关于x的一元二次方程x2+bx-6=0有一个根是x=2,求b的值及方程的另一个根.18. 如图,在Rt△ABC中,∠C=90°,将△ABC绕点A逆时针旋转,得到△ADE,点E在AB上,若∠ABC=32°,求∠ABD的大小.
 19. 有4张看上去无差别的卡片,上面分别写着数字1,2,3,6,随机抽取1张卡片后放回并混在一起,再随机抽取一张卡片.(1)、直接写出抽取的两张卡片上的数字相同的概率;(2)、请用列表或画树状图法求第一次取出的数字是第二次取出的数字的整数倍的概率,20. 如图,在⊙O中,弦AB,CD相交于点M,且AB=CD.
19. 有4张看上去无差别的卡片,上面分别写着数字1,2,3,6,随机抽取1张卡片后放回并混在一起,再随机抽取一张卡片.(1)、直接写出抽取的两张卡片上的数字相同的概率;(2)、请用列表或画树状图法求第一次取出的数字是第二次取出的数字的整数倍的概率,20. 如图,在⊙O中,弦AB,CD相交于点M,且AB=CD.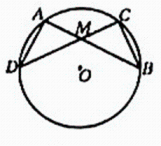 (1)、求证:AD=BC;(2)、连接OM,BD,若BD是⊙O的直径,AB=2AD=8,求OM的长.21. 如图是由小正方形组成的8×8网格,每个小正方形的顶点叫做格点.⊙O经过格点A,B,点C为⊙O与格线的交点,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)、求证:AD=BC;(2)、连接OM,BD,若BD是⊙O的直径,AB=2AD=8,求OM的长.21. 如图是由小正方形组成的8×8网格,每个小正方形的顶点叫做格点.⊙O经过格点A,B,点C为⊙O与格线的交点,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.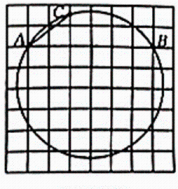 (1)、画出该圆的圆心O,并画弦AD,使AD平分∠BAC;(2)、先将弦AC绕点A顺时针旋转90°得到线段AF,再在圆上画点E,使AC=BE.22. 现要修建一条隧道,其截面为抛物线型,如图所示,线段AB表示水平的路面,O为AB的中点,以O为坐标原点,以AB所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.根据设计要求:抛物线底面宽度AB=12米,该抛物线的顶点P到AB的距离为9米.
(1)、画出该圆的圆心O,并画弦AD,使AD平分∠BAC;(2)、先将弦AC绕点A顺时针旋转90°得到线段AF,再在圆上画点E,使AC=BE.22. 现要修建一条隧道,其截面为抛物线型,如图所示,线段AB表示水平的路面,O为AB的中点,以O为坐标原点,以AB所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.根据设计要求:抛物线底面宽度AB=12米,该抛物线的顶点P到AB的距离为9米. (1)、求抛物线的解析式:(2)、现需在这一隧道内壁上同一高度安装照明灯,即在该抛物线上的点M,N处分别安装照明灯.已知照明灯M,N的水平距离为10米,求照明灯距地面的高度:(3)、如图,现需在隧道上方安装一块高度为1米、宽度为3米的LED电子显示屏CDEF,为确保行车安全,要求电子显示屏距地面至少6米,并且距左右墙需各留至少1米的安全距离,试通过计算说明能否满足安装设计要求.
(1)、求抛物线的解析式:(2)、现需在这一隧道内壁上同一高度安装照明灯,即在该抛物线上的点M,N处分别安装照明灯.已知照明灯M,N的水平距离为10米,求照明灯距地面的高度:(3)、如图,现需在隧道上方安装一块高度为1米、宽度为3米的LED电子显示屏CDEF,为确保行车安全,要求电子显示屏距地面至少6米,并且距左右墙需各留至少1米的安全距离,试通过计算说明能否满足安装设计要求.
23.
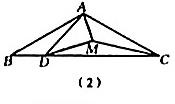
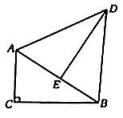
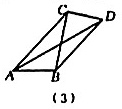 (1)、问题背景如图,在等腰△ABC中,AB=AC,∠BAC=a,D为BC边上的一动点,将线段AD绕点A逆时针旋转a得到线段AE,连接CE.求证:BD=CE;(2)、尝试运用如图,在等腰△ABC中,AB=AC,∠BAC=120°,D为BC边上的一动点,以AD为斜边在AD右侧构造Rt△AMD,∠AMD=90°,∠ADM=30°.连接CM,设BD=a,CD=b,求△CDM的面积(用a,b表示);(3)、拓展创新如图,在Rt△BCD中,∠BCD=90°,∠CBD=30°,∠BAD=30°,AB=1, , 直接写出△ABC的面积.24. 如图,抛物线y=ax2+bx+c经过原点,且顶点坐标为(2,-4).
(1)、问题背景如图,在等腰△ABC中,AB=AC,∠BAC=a,D为BC边上的一动点,将线段AD绕点A逆时针旋转a得到线段AE,连接CE.求证:BD=CE;(2)、尝试运用如图,在等腰△ABC中,AB=AC,∠BAC=120°,D为BC边上的一动点,以AD为斜边在AD右侧构造Rt△AMD,∠AMD=90°,∠ADM=30°.连接CM,设BD=a,CD=b,求△CDM的面积(用a,b表示);(3)、拓展创新如图,在Rt△BCD中,∠BCD=90°,∠CBD=30°,∠BAD=30°,AB=1, , 直接写出△ABC的面积.24. 如图,抛物线y=ax2+bx+c经过原点,且顶点坐标为(2,-4).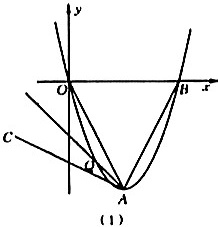
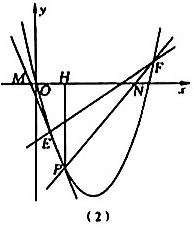 (1)、求抛物线的解析式(2)、如图(1),B是抛物线与x轴的另一交点,将线段AB绕抛物线顶点A逆时针旋转90°得到线段AC,若AQ平分∠OAC交抛物线于点Q.求点Q的坐标;(3)、如图(2),过点H(1,0)作PH⊥x轴交抛物线于点P,E,F为抛物线上两动点(点E在点P左侧,点F在点P右侧),直线PE,PF分别交x轴于点M,N.若HM·HN=3,求证:直线EF过一个定点.
(1)、求抛物线的解析式(2)、如图(1),B是抛物线与x轴的另一交点,将线段AB绕抛物线顶点A逆时针旋转90°得到线段AC,若AQ平分∠OAC交抛物线于点Q.求点Q的坐标;(3)、如图(2),过点H(1,0)作PH⊥x轴交抛物线于点P,E,F为抛物线上两动点(点E在点P左侧,点F在点P右侧),直线PE,PF分别交x轴于点M,N.若HM·HN=3,求证:直线EF过一个定点.