陕西省西安市雁塔区重点中学2024年中考数学一模试卷

试卷更新日期：2024-03-25 类型：中考模拟

进入出卷网下载

一、选择题（共8小题，每小题3分，计24分．每小题只有一个选项是正确的）

1. 抛物线y＝x²-2的顶点坐标是（）

A、（-2，0） B、（2，0） C、（0，2） D、（0，-2）

查看试题解析
2. 如图，在Rt△ABC中，∠C＝90°，BC＝3AC，则tanB＝（）

A、 $\frac{1}{3}$ B、3 C、 $\frac{\sqrt{10}}{10}$ D、 $\frac{3 \sqrt{10}}{10}$

查看试题解析
3. 下列说法：①三点确定一个圆，②平分弦（不是直径）的直径垂直于弦，③相等的圆心角所对的弦相等，④三角形的外心到三个顶点的距离相等，其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 图1是一个地铁站入口的双翼闸机．如图2，它的双翼展开时，双翼边缘的端点A与B之间的距离为12cm，双翼的边缘AC＝BD＝64cm，且与闸机侧立面夹角∠PCA＝∠BDQ＝30°．当双翼收起时，可以通过闸机的物体的最大宽度为（）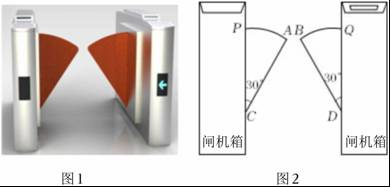

A、76cm B、（64 $\sqrt{2}$ +12）cm C、（64 $\sqrt{3}$ +12）cm D、64cm

查看试题解析
5. 在△ABC中，∠C＝90°，∠A＝60°，BC＝4，若⊙C与AB相离，则半径为r满足（）

A、r＞2 B、r＜2 C、0＜r＜2 D、0＜r＜2 $\sqrt{3}$

查看试题解析
6. 如图，在一张Rt△ABC纸片中，∠ACB＝90°，BC＝5，AC＝12，⊙O是它的内切圆．小明用剪刀沿着⊙O的切线DE剪下一块三角形ADE，则△ADE的周长为（　　）

A、19 B、17 C、22 D、20

查看试题解析
7. 扇子最早称“翣”，在我国已有两千多年历史．“打开半个月亮，收起兜里可装，来时荷花初放，去时菊花正黄．”这则谜语说的就是扇子．如图，一竹扇完全打开后，外侧两竹条AB，AC夹角为135°，AB的长为30cm，贴纸部分的宽BD为20cm，则扇面面积为（）

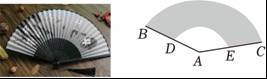A、 $\frac{375}{2} π$ cm² B、300πcm² C、600πcm² D、30πcm²

查看试题解析
8. 若二次函数y＝x²+2 $\sqrt{5}$ x+3m-1的图象只经过第一、二、三象限，则m满足的条件一定是（）

A、m＞ $\frac{1}{3}$ B、m＜2 C、m＜-2或m≥- $\frac{1}{3}$ D、 $\frac{1}{3}$ ≤m＜2

查看试题解析

二、填空题（共6小题，每小题3分，计18分）

9. 在△ABC中，若|sinA- $\frac{1}{2}$ |+（ $\frac{\sqrt{2}}{2}$ -cosB）²＝0，则∠C的度数是．

查看试题解析
10. 在Rt△ABC中，若两直角边长为6cm、8cm，则它的外接圆的面积为．

查看试题解析
11. 如图，抛物线y＝ax²+bx+c的一部分经过点A（-1，0），且其对称轴是直线x＝2，则一元二次方程ax²+bx+c＝0的根是．

查看试题解析
12. 如图，某品牌扫地机器人的形状是“莱洛三角形”，它的三“边”分别是以等边三角形的三个顶点为圆心，边长为半径的三段圆弧．若该等边三角形的边长为3，则这个“莱洛三角形”的周长是．

查看试题解析
13. 已知抛物线C₁：y＝2x²-4x-1，抛物线C₂是由抛物线C₁向右平移3个单位得到的，那我们可以得到抛物线C₁和抛物线C₂一定关于某条直线对称，则这条直线为．

查看试题解析
14. 如图，⊙M的半径为4，圆心M的坐标为（6，8），点P是⊙M上的任意一点，PA⊥PB，且PA、PB与x轴分别交于A、B两点．若点A、点B关于原点O对称，则当AB取最大值时，点A的坐标为．

查看试题解析

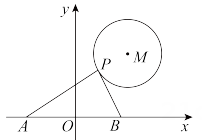
三、解答题（共11小题，计78分．解答题应写出过程）

15. 计算：

(1)、2cos60°+|1-2sin45°|+（ $\frac{1}{2}$ ）⁰ ．

(2)、 $\sqrt{1 - 2 t a n 60 ° + t a n^{2} 60 °}$ -tan60°．

查看试题解析
16. 如图，点P是⊙O外一点．请利用尺规过点P作⊙O的一条切线PE．（保留作图痕迹，不要求写作法和证明）

查看试题解析
17. 如图，正六边形ABCDEF内接于⊙O．

(1)、若P是 $\overset{⌢}{C D}$ 上的动点，连接BP，FP，求∠BPF的度数；

(2)、已知△ADF的面积为 $2 \sqrt{3}$ ，求⊙O的面积．

查看试题解析
18. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $C D$ ， $C H$ 分别是 $A B$ 边上的中线和高， $B C = 6$ ， $c o s ∠ A C D = \frac{4}{5}$ ，求 $A B$ ， $C H$ 的长．

查看试题解析
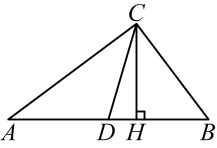19. 如图，AB是⊙O的直径，弦CD⊥AB于点E，点P在⊙O上，∠1＝∠C，

(1)、求证：CB∥PD；

(2)、若BC＝3，∠C＝30°，求⊙O的直径．

查看试题解析
20. 如图，小华和同伴秋游时，发现在某地小山坡的点E处有一棵小树，他们想利用皮尺、倾角器和平面镜测量小树到山脚下的距离（即DE的长度），小华站在点B处，让同伴移动平面镜至点C处，此时小华在平面镜内可以看到点E．且测得BC＝3米，CD＝28米．∠CDE＝127°．已知小华的眼睛到地面的距离AB＝1.5米，请根据以上数据，求DE的长度．（参考数据： $s i n 37 ° \approx \frac{3}{5}$ ， $t a n 37 ° \approx \frac{3}{4}$ ）

查看试题解析
21. 有一座抛物线型拱桥，在正常水位时水面宽AB＝20m，当水位上升3m时，水面宽CD＝10m．按如图所示建立平面直角坐标系．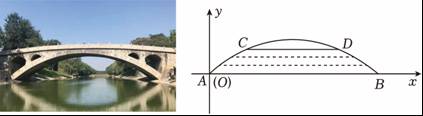

(1)、求此抛物线的函数表达式；

(2)、有一条船以6km/h的速度向此桥径直驶来，当船距离此桥36km时，桥下水位正好在AB处，之后水位每小时上涨0.3m，为保证安全，当水位达到距拱桥最高点2m时，将禁止船只通行．如果该船的速度不变，那么它能否安全通过此桥？

查看试题解析
22. 如图所示，要在底边，BC＝160cm，高AD＝120cm的△ABC铁皮余料上，截取一个矩形EFGH，使点H在AB上，点G在AC上，点E、F在BC上，AD交HG于点M．

(1)、设矩形EFGH的长HG＝y，宽HE＝x，确定y与x的函数关系式；

(2)、设矩形EFGH的面积为S，当x为何值时，矩形EFGH的面积S最大？并求出最大值．

查看试题解析
23. 如图，点O在∠APB的平分线上，⊙O与PA相切于点C．

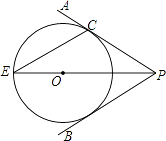(1)、求证：直线PB与⊙O相切；

(2)、PO的延长线与⊙O交于点E．若⊙O的半径为3，PC=4．求弦CE的长．

查看试题解析
24. 已知抛物线y＝ax²+bx-4经过点A（-2，0），B（4，0），与y轴的交点为C．

(1)、求该抛物线的函数表达式；

(2)、若点P是该抛物线上一点，且位于其对称轴l的左侧，过点P分别作l，x轴的垂线，垂足分别为M，N，连接MN．若△PMN和△OBC相似，求点P的坐标．

查看试题解析
25. 问题发现

(1)、在△ABC中，AB＝2，∠C＝60°，则△ABC面积的最大值为；

(2)、如图1，在四边形ABCD中，AB＝AD＝6，∠BCD＝∠BAD＝90°，AC＝8，求BC+CD的值．

(3)、问题解决
有一个直径为60cm的圆形配件⊙O，如图2所示．现需在该配件上切割出一个四边形孔洞OABC，要求∠O＝∠B＝60°，OA＝OC，并使切割出的四边形孔洞OABC的面积尽可能小．试问，是否存在符合要求的面积最小的四边形OABC？若存在，请求出四边形OABC面积的最小值及此时OA的长；若不存在，请说明理由．

查看试题解析