云南省2024年中考数学模拟试卷(一)
试卷更新日期:2024-03-24 类型:中考模拟
一、选择题
-
1. 的算术平方根是( )A、﹣2 B、±2 C、 D、22. 中华文明,源远流长:中华汉字,寓意深广.下列四个选项中,是轴对称图形的为( )A、
 B、
B、 C、
C、 D、
D、 3. 若点是反比例函数图象上一点,则常数的值为( )A、3 B、 C、 D、4. 按一定规律排列的单项式: , 第个单项式是( )A、 B、 C、 D、5. 如图,平行四边形 的对角线 , 相交于点O,E是 的中点,则 与 的面积的比等于( )
3. 若点是反比例函数图象上一点,则常数的值为( )A、3 B、 C、 D、4. 按一定规律排列的单项式: , 第个单项式是( )A、 B、 C、 D、5. 如图,平行四边形 的对角线 , 相交于点O,E是 的中点,则 与 的面积的比等于( )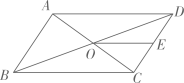 A、 B、 C、 D、6. 若一元二次方程 有两个不相等的实数根,则实数a的取值范围是( )A、 B、 C、 且 D、 且7. 如图,是的直径,是上一点.若 , 则( )
A、 B、 C、 D、6. 若一元二次方程 有两个不相等的实数根,则实数a的取值范围是( )A、 B、 C、 且 D、 且7. 如图,是的直径,是上一点.若 , 则( )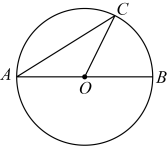 A、 B、 C、 D、8. 用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套罐头盒.现有36张白铁皮,设用x张制盒身,y张制盒底,恰好配套制成罐头盒.则下列方程组中符合题意的是( )A、 B、 C、 D、9. 中国是最早采用正负数表示相反意义的量,并进行负数运算的国家.若零上10℃记作+10℃,则零下10℃可记作( )A、10℃ B、0℃ C、-10 ℃ D、-20℃10. 如图,已知E(﹣4,2),F(﹣1,﹣1),以原点O为位似中心,按比例尺2:1把△EFO缩小,则E点对应点E′的坐标为( )
A、 B、 C、 D、8. 用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套罐头盒.现有36张白铁皮,设用x张制盒身,y张制盒底,恰好配套制成罐头盒.则下列方程组中符合题意的是( )A、 B、 C、 D、9. 中国是最早采用正负数表示相反意义的量,并进行负数运算的国家.若零上10℃记作+10℃,则零下10℃可记作( )A、10℃ B、0℃ C、-10 ℃ D、-20℃10. 如图,已知E(﹣4,2),F(﹣1,﹣1),以原点O为位似中心,按比例尺2:1把△EFO缩小,则E点对应点E′的坐标为( )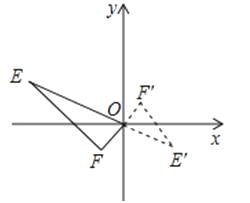 A、(2,1) B、( , ) C、(2,﹣1) D、(2,﹣)11. 如图,在平行四边形中,对角线 , 相交于点 , 点是的中点,连接若的面积为 , 则平行四边形的面积为( )
A、(2,1) B、( , ) C、(2,﹣1) D、(2,﹣)11. 如图,在平行四边形中,对角线 , 相交于点 , 点是的中点,连接若的面积为 , 则平行四边形的面积为( ) A、 B、 C、 D、12. 如图,在同一平面直角坐标系中,直线与双曲线相交于点和点 , 则当时,的取值范围是( )
A、 B、 C、 D、12. 如图,在同一平面直角坐标系中,直线与双曲线相交于点和点 , 则当时,的取值范围是( )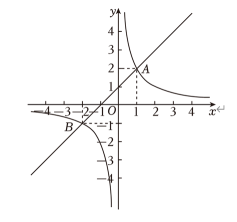 A、或 B、 C、或 D、或
A、或 B、 C、或 D、或二、填空题
-
13. ﹣9的相反数是.14. 要使有意义,的取值范围是 .15. 如图所示,半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动.且滚动至扇形O′A′B′处,则顶点O所经过的路线总长是
 16. 若△ADE∽△ACB,且= , DE=10,则BC= .
16. 若△ADE∽△ACB,且= , DE=10,则BC= .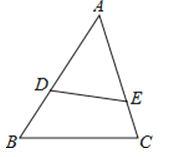
三、解答题
-
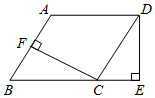
17. 先化简,再求值: , 其中x是这四个数中合适的数.18. 如图,在▱ABCD中,CF⊥AB于点F , 过点D作DE⊥BC交BC的延长线于点E , 且CF=DE .
求证:BF=CE .
 19. 我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具—“三分角器”.图1是它的示意图,其中如与半圆O的直径BC在同一直线上,且AB的长度与半圆的半径相等;DB与AC垂直于点B,DB足够长.使用方法如图2所示,若要把∠MEN三等分,只需适当放置三分角器,使DB经过∠MEN的顶点E,点A落在边EM上,半圆O与另一边EN恰好相切,切点为F,则EB,EO就把∠MEN三等分了.为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.
19. 我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具—“三分角器”.图1是它的示意图,其中如与半圆O的直径BC在同一直线上,且AB的长度与半圆的半径相等;DB与AC垂直于点B,DB足够长.使用方法如图2所示,若要把∠MEN三等分,只需适当放置三分角器,使DB经过∠MEN的顶点E,点A落在边EM上,半圆O与另一边EN恰好相切,切点为F,则EB,EO就把∠MEN三等分了.为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.已知:如图2,点A,B,O,C在同一直线上, , 垂足为点B,半圆O与EN相切于点F,........... .
求证:EB,EO是∠MEN三等分线.
 20. 党的二十大是在全党全国各族人民迈上全面建设社会主义现代化国家新征程、向第二个百年奋斗目标进军的关键时刻召开的一次十分重要的大会,是一次高举旗帜、凝聚力量、团结奋进的大会为深入学习贯彻党的二十大精神,某校组织全体名学生参加了“学习二十大,水远跟党走,奋进新征程”的知识竞赛活动满分分 , 并在竞赛结束后对全校一半左右的学生进行表扬奖励该校某老师为了解全校学生竞赛分数情况,采用简单随机抽样的方法即每名学生被抽到的可能性相等的抽样方法在全校学生的竞赛分数中抽取了名学生的竞赛分数进行统计竞赛分数用表示,共分成五组: , , , , , 并绘制了如图甲、乙两幅不完整的统计图:
20. 党的二十大是在全党全国各族人民迈上全面建设社会主义现代化国家新征程、向第二个百年奋斗目标进军的关键时刻召开的一次十分重要的大会,是一次高举旗帜、凝聚力量、团结奋进的大会为深入学习贯彻党的二十大精神,某校组织全体名学生参加了“学习二十大,水远跟党走,奋进新征程”的知识竞赛活动满分分 , 并在竞赛结束后对全校一半左右的学生进行表扬奖励该校某老师为了解全校学生竞赛分数情况,采用简单随机抽样的方法即每名学生被抽到的可能性相等的抽样方法在全校学生的竞赛分数中抽取了名学生的竞赛分数进行统计竞赛分数用表示,共分成五组: , , , , , 并绘制了如图甲、乙两幅不完整的统计图:
其中组中竞赛分数最高的是 , 组中竞赛分数最低的是 .
(1)、在抽取的学生中,竞赛分数达到优秀的人数为 ,竞赛分数的中位数为 ;
(2)、试估计全校学生竞赛分数不及格的人数,若该校某同学的竞赛分数为分,试估计该同学是否能获得表扬奖励.21. 如图,四边形是矩形,和相交于点 , 过点作 , 且 , 连接点是线段上与点 , 点不重合的一个动点,过点分别作 , 的垂线,垂足分别为点 , 点 . (1)、求证:四边形是菱形;
(1)、求证:四边形是菱形;
(2)、若 , 则在点的运动中,的值是否会发生变化?若不变化,求出其值;若变化,请说明理由.22. 部分手机生产商以环保为名销售手机时不再搭配充电器,某电商看准时机,购进一批慢充充电器和快充充电器,已知该电商销售个慢充充电器和个快充充电器的利润为元;销售个慢充充电器和个快充充电器的利润为元.(1)、求每个慢充充电器和每个快充充电器的销售利润;
(2)、该电商购进两种类型的充电器共个,其中快充充电器的进货量不超过慢充充电器的倍,设电商购进慢充充电器个,这批充电器的销售总利润为元该电商怎样购进两种类型的充电器,才能使销售总利润最大?最大利润是多少元?23. 五一小长假期间,小林和小云一起来到昆明旅游,晚上他们打算去特色街吃饭他们看到满大街各式各样的美食,却不知道选择哪一个,于是通过抽卡片的游戏来决定吃什么,他们制作了四张背面完全相同的卡片,在正面上分别写着:过桥米线:野生菌火锅:鲜花饼:汽锅鸡,将这四张卡片背面朝上,放置在水平桌面上,洗匀放好小林先从四张卡片中随机抽取一张,放回洗匀后,小云再从四张卡片中随机抽取一张.(1)、小林抽到卡片正面写着汽锅鸡的概率是 ;
(2)、请利用列表或画树状图的方法,求两个人抽到同一种特色美食的概率.24. 如图,抛物线y= x2+mx+n与直线y=﹣ x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0). (1)、求抛物线的解析式和tan∠BAC的值;(2)、在(1)条件下:
(1)、求抛物线的解析式和tan∠BAC的值;(2)、在(1)条件下:(Ⅰ)P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
(Ⅱ)设E为线段AC上一点(不含端点),连接DE,一动点M从点D出发,沿线段DE以每秒一个单位速度运动到E点,再沿线段EA以每秒 个单位的速度运动到A后停止,当点E的坐标是多少时,点M在整个运动中用时最少?