河北省2024年中考数学模拟试卷(四)
试卷更新日期:2024-03-24 类型:中考模拟
一、单选题
-
1. 计算 , 则?=( )A、1 B、5 C、6 D、92. 在中,是的中线.看到图形,甲、乙、丙、丁四名同学给出四个不同的结论,其中正确的是( )
甲:
乙:
丙:
丁:
 A、甲 B、乙 C、丙 D、丁3. 若 , 则的值为( )A、 B、 C、 D、4. 如图是嘉嘉把纸折叠后剪出的图案,将剪纸展开后得到的图案是( )
A、甲 B、乙 C、丙 D、丁3. 若 , 则的值为( )A、 B、 C、 D、4. 如图是嘉嘉把纸折叠后剪出的图案,将剪纸展开后得到的图案是( )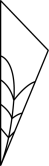 A、
A、 B、
B、 C、
C、 D、
D、 5. 互联网已经进入时代,应用网络下载一个的文件只需要秒,将数据用科学记数法表示应为( )A、 B、 C、 D、6. 数学课上进行小组合作式学习,老师让小组成员的2号同学写出5个常错的式子,4号同学进行判断,则判断正确的个数是( )
5. 互联网已经进入时代,应用网络下载一个的文件只需要秒,将数据用科学记数法表示应为( )A、 B、 C、 D、6. 数学课上进行小组合作式学习,老师让小组成员的2号同学写出5个常错的式子,4号同学进行判断,则判断正确的个数是( )(1)(×)
(2)(×)
(3)(×)
(4)(√)
(5)(×)
A、5个 B、4个 C、3个 D、2个7. 如图,圆柱的底面直径为AB,高为AC.一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )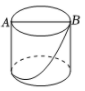 A、
A、 B、
B、 C、
C、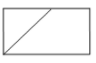 D、
D、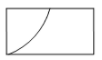 8. 不能被下列数整除的是( )A、 B、 C、 D、9. 如图,在正方形网格中,与位似,则下列说法正确的是( )
8. 不能被下列数整除的是( )A、 B、 C、 D、9. 如图,在正方形网格中,与位似,则下列说法正确的是( ) A、位似中心是点 B、位似中心是点 C、位似比为 D、位似比为10. 如图,在平面直角坐标系中有 , , , 四个点,其中恰有三点在反比例函数的图象上.根据图中四点的位置,判断这四个点中不在函数的图象上的点是( )
A、位似中心是点 B、位似中心是点 C、位似比为 D、位似比为10. 如图,在平面直角坐标系中有 , , , 四个点,其中恰有三点在反比例函数的图象上.根据图中四点的位置,判断这四个点中不在函数的图象上的点是( )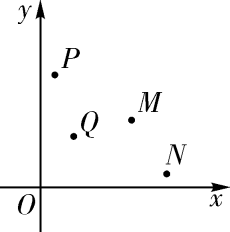 A、点 B、点 C、点 D、点11. 一次数学测试,某小组5名同学的成绩统计如下(有两个数据被遮盖):
A、点 B、点 C、点 D、点11. 一次数学测试,某小组5名同学的成绩统计如下(有两个数据被遮盖):组员
甲
乙
丙
丁
戊
平均成绩
众数
得分
则被遮盖的两个数据依次是( )
A、 B、 C、 D、12. 如图,在平面直角坐标系中,的顶点为 , , . 以点为位似中心,在第三象限内作与的位似比为的位似图形 , 则点的坐标为( ) A、 B、 C、 D、13. 老师在微信群发了这样一个图:以线段为边作正五边形和正三角形 , 连接 , 交于点 , 下列四位同学的说法错误的是( )
A、 B、 C、 D、13. 老师在微信群发了这样一个图:以线段为边作正五边形和正三角形 , 连接 , 交于点 , 下列四位同学的说法错误的是( )
甲 乙 是的垂直平分线
丙 是等腰三角形
丁 与平行
A、甲 B、乙 C、丙 D、丁14. 如图,四边形中,与不平行, , 分别是、的中点, , , 则的长可能是( ) A、4 B、6 C、8 D、1015. 如图,是的外接圆,在弧上找一点M,使点M平分弧 . 以下是甲乙丙三种不同的作法:
A、4 B、6 C、8 D、1015. 如图,是的外接圆,在弧上找一点M,使点M平分弧 . 以下是甲乙丙三种不同的作法:
作法正确的个数是( )
A、0个 B、1个 C、2个 D、3个16. 如图,把两块全等的直角三角板和叠放在一起,使三角板的锐角顶点与三角板的斜边中点重合,经过点 , 其中 , , , 把三角板固定不动,让三角板绕点逆时针旋转,旋转角为 . 其中 . 设射线与射线相交于点 , 线段与线段相交于点 . 给出下面三个结论:①;②的值不变,为8;③当时,设 , 两块三角板重叠部分的面积为 . 其中正确的是( )
 A、只有①与② B、只有①与③ C、只有②与③ D、①②③
A、只有①与② B、只有①与③ C、只有②与③ D、①②③二、填空题
-
17. 如图,直线 , , , 则 .
 18. 如图,已知在中, , , 点P是的中点,过点P的直线与交于点Q,依据尺规作图痕迹解决下列问题.
18. 如图,已知在中, , , 点P是的中点,过点P的直线与交于点Q,依据尺规作图痕迹解决下列问题. (1)、与是否平行?(填“是”或“否”);(2)、的周长为 .19. 如图,在中, , , , D是边上一点,线段绕点D顺时针旋转得到 , 连接 , 若F是的中点.
(1)、与是否平行?(填“是”或“否”);(2)、的周长为 .19. 如图,在中, , , , D是边上一点,线段绕点D顺时针旋转得到 , 连接 , 若F是的中点. (1)、与的位置关系是;(2)、当点F在上时,;(3)、的最小值为 .
(1)、与的位置关系是;(2)、当点F在上时,;(3)、的最小值为 .三、解答题
-
20. 已知P=A·B-M.(1)、若A=(-3)0 , B= , M=|-1|,求P的值;(2)、若A=3,B=x,M=5x-1,且P≤3,求x的取值范围,并在如图所示的数轴上表示出解集.
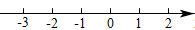 21. 定义:对于一个三位正整数,如果十位数字恰好等于百位数字与个位数字之和的一半,我们称这个三位正整数为“半和数”.
21. 定义:对于一个三位正整数,如果十位数字恰好等于百位数字与个位数字之和的一半,我们称这个三位正整数为“半和数”.例如,三位正整数234,因为 , 所以234是“半和数”.
(1)、判断147是否为“半和数”,并说明理由;(2)、小林列举了几个“半和数”:111、123、234、840…,并且她发现: , , , …,所以她猜测任意一个“半和数”都能被3整除.小林的猜想正确吗?若正确,请你帮小林说明该猜想的正确性;若错误,说明理由.22. 如图1,在中, , 为线段上一点,以为圆心,长为半径的圆与边 , 分别交于 , 两点,过点作的切线,交于点. (1)、求证: .(2)、如图2,若为的中点.
(1)、求证: .(2)、如图2,若为的中点.①探究与的数量关系,并说明理由;
②连接 , 若 , , 求阴影部分的面积.
23. 如图,在平面直角坐标系中,直线过点 , 点 , 直线:与轴交于点 .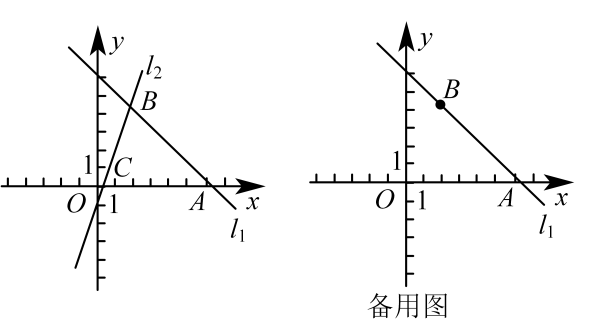 (1)、求直线的函数表达式.(2)、若直线过点 .
(1)、求直线的函数表达式.(2)、若直线过点 .①求的值.
②若点在内部,求的取值范围.
(3)、直线与直线和直线分别交于点、 , 当线段的长不大于4时,求的取值范围.24. 为弘扬民族传统体育文化,某校将传统游戏“滚铁环”列入了校运动会的比赛项目.滚铁环器材由铁环和推杆组成.小明对滚铁环的启动阶段进行了研究,如图,滚铁环时,铁环⊙O与水平地面相切于点C,推杆AB与铅垂线AD的夹角为∠BAD,点O,A,B,C,D在同一平面内.当推杆AB与铁环⊙O相切于点B时,手上的力量通过切点B传递到铁环上,会有较好的启动效果.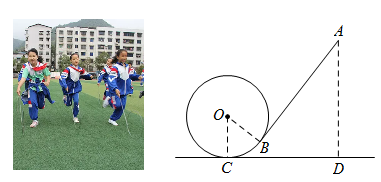 (1)、求证:∠BOC+∠BAD=90°.(2)、实践中发现,切点B只有在铁环上一定区域内时,才能保证铁环平稳启动.图中点B是该区域内最低位置,此时点A距地面的距离AD最小,测得 . 已知铁环⊙O的半径为25cm,推杆AB的长为75cm,求此时AD的长.25. 如图,抛物线:与轴交于、两点(点在点的左侧),与轴交于点且 , 点为抛物线的对称轴右侧图象上的一点(不含顶点).
(1)、求证:∠BOC+∠BAD=90°.(2)、实践中发现,切点B只有在铁环上一定区域内时,才能保证铁环平稳启动.图中点B是该区域内最低位置,此时点A距地面的距离AD最小,测得 . 已知铁环⊙O的半径为25cm,推杆AB的长为75cm,求此时AD的长.25. 如图,抛物线:与轴交于、两点(点在点的左侧),与轴交于点且 , 点为抛物线的对称轴右侧图象上的一点(不含顶点).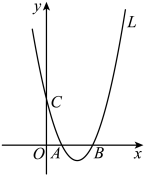 (1)、的值为 , 抛物线的顶点坐标为;(2)、设抛物线在点和点之间的部分(含点和点)的最高点与最低点的纵坐标之差为 , 求关于的函数表达式,并写出自变量的取值范围;(3)、若点的坐标满足时,连接 , 将直线与抛物线围成的封闭图形记为 .
(1)、的值为 , 抛物线的顶点坐标为;(2)、设抛物线在点和点之间的部分(含点和点)的最高点与最低点的纵坐标之差为 , 求关于的函数表达式,并写出自变量的取值范围;(3)、若点的坐标满足时,连接 , 将直线与抛物线围成的封闭图形记为 .①求点的坐标;
②直接写出封闭图形的边界上的整点(横、纵坐标都是整数)的个数.
26. 如图,中, , , , 点P从点C出发,沿的方向运动,点Q从点C出发,沿射线的方向运动,过点Q且与垂直的直线也随之运动.点P的速度是每秒4个单位,点Q的速度是每秒3个单位.点P与点Q同时出发,当点P运动到点B时同时停止.连接 , 设运动时间为t,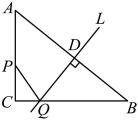 (1)、当点P在上,且不与点C,A重合(即)时,
(1)、当点P在上,且不与点C,A重合(即)时,①求证:;
②当t为何值时与全等.
(2)、直接写出当t为何值时,点P到直线的距离是8.